Порядок виконання роботи

А. При пiдготовцi:

1.Ознайомитися з методами квадратичної iнтерполяцiї функцiй, поданих у виглядi таблиць [Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. - М.: Наука, 1972.-с.100-127 ].

2.В залежностi вiд можливого положення заданої точки (струм i₀, див.таблицю 8.1 лабораторної роботи №8) вибрати дві придатнi iнтерполяцiйнi формули (iз наведених у цiй роботi, у теоретичнiй частинi). Не виключається використання iнших iнтерполяцiйних формул.

3.Розробити алгоритм розрахунку опору постiйному струму i диференцiйного опору (опору змiнному струму) нелiнiйного елемента, вольт-амперна характеристика U=f(i) якого задана у виглядi таблицi (таблиця 8.1), використовуючи квадратичну iнтерполяцiю у заданiй точцi i₀.

4.На рисунку з вольт-амперною характеристикою нелiнiйного елемента лабораторної роботи №8 виконати графiчнi побудови, якi пояснюють розроблений алгоритм розрахунку опорiв. Оцінити значення опорів.

5.Написати програму розрахунку значень опорiв нелiнiйного елемента у заданiй точцi його вольт-амперної характеристики.Нелінійний елемент описати структурою,у якій представлені значення струму, напруги, опору постійному струму та диференційного опору:

struct nel_element

{

float current;

float voltage;

float cont_resistance;

float alt_resistance;

};

Розрахунок значень елементів структури провести у зовнішній функції, яка отримує масиви струмів і напруг та значення струму і₀ ,а повертає структуру нелінійного елемента (для кожної інтерполяційної формули своя зовнішня функція).Чисельні результати розрахунків вивести на екран та у файл на диску L.Програма повинна складатися із трьох модулів-файлів: заголовного файлу name.h (опис структури, прототипи функцій) , файлу name.cpp з означеннями функцій та файлу –користувача name1.cpp з головною функцією main. Для виконання такої програми треба буде створити файл проекту name.prj.

В. У лабораторiї:

1. Виконати пiдготовлену програму i отримати потрiбнi результати.

2. Порiвняти значення опору постiйному струму, знайдене у лабораторнiй роботi №8, iз отриманим значенням опору постiйному струму. Зробити належнi висновки, оцiнити достовiрнiсть отриманих результатiв, їх похибку.

Змiст звiту:

1. Програма.

2. Блок-схема алгоритму.

3. Графiчнi побудови.

4. Результати розрахунку, їх оцiнка.

5. Висновки по роботi.

Теоретична частина

Рис. 9.1

Рис.9.1

На рис. 9.1 зображена функцiя y=f(x), яка визначається дискретними значеннями x_i, y_i (i =1,...n). В залежностi вiд положення заданої точки x₀ квадратична iнтерполяцiя виконується згiдно однiєї iз запропонованих далi формул.

1. Симетрична iнтерполяцiйна формула Бесселя

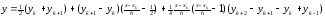
використовується для iнтерполяцiї у серединi таблицi при q=(x₀-x_k)/h, наближених до 0.5, практично для 0.25  q  0.75, (x₀ > x_k; h = x_k+1- x_k).

2. Перша iнтерполяцiйна формула Ньютона

застосовується при iнтерполяцiї на початку таблицi у точках, близьких до x_k : q=(x₀-x_k)/h  0.3, (x₀>x_k).

3. Друга iнтерполяцiйна формула Ньютона

використовується при iнтерполяцiї в кiнцi таблицi бiля x_k+3: |q|  0.3

( q=(x₀-x_k+3)/h, x₀<x_k+3 )

4. Перша інтерполяційна формула Гауса

застосовується при інтерполяції у середині таблиці у точках, близьких до x_k: (q=(x₀-x_k)/h 0,3; x₀>x_k).

5.Друга інтерполяційна формула Гаусса

використовується при інтерполяції у середині таблиці поблизу х_k

(q=(x₀-x_k-1)/h  0,7; x₀ < x_k)

6. Інтерполяційна формала Стірлінга

Забезпечує інтерполяцію також у середині таблиці для малих g, практично

q  0,25 (q=|x₀-x_k|/h)

7. Iнтерполяцiйна формула Лагранжа

використовується для довiльно заданих вузлiв iнтерполяцiї.

Наведенi у пп.1...6 формули придатнi тiльки у разi рiвновiддалених вузлiв iнтерполяцii. Формула Лагранжа застосовується для iнтерполяцiї у серединi таблицi поблизу x_k:

Перша похiдна функцiї dy/dx визначається за допомогою аналiтичного диференцювання iнтерполяцiйної формули ручним способом з наступним чисельним розрахунком на ПК.

Опiр нелiнiйного елемента з вольт-амперною характеристикою u=f(i) визначається:

опiр сталому струму Rc = u / i , (i = i₀) ;

опiр змiнному струму Ra = du / di , (i = i₀). (диференцiйний)

Лабораторна робота № 11

РОЗРАХУНОК СХОДИНКОВОГО ЕЛЕКТРИЧНОГО КОЛА ПОСТIЙНОГО СТРУМУ З ДОВIЛЬНОЮ КIЛЬКIСТЮ ЛАНОК

Мета роботи - складання програм розрахунку струмiв у всiх гілках складного електричного кола i напруги на його виходi.