
- •Методические указания
- •1 Ветвление
- •1.1 Бинарное ветвление
- •1.2 Ветвление по компонентам
- •2 Оценка
- •3 Рекорд
- •5 Схема метода ветвей и границ
- •6 Стратегия
- •7 Метод ветвей и границ для решения задачи целочисленного линейного программирования
- •7.1 Ветвление
- •7.2 Вычисление оценки
- •7.3 Тест
- •7.4 Примеры использования метода ветвей и границ для решения задач целочисленного линейного программирования
- •7.5 Задания для самостоятельной работы
- •8 Метод ветвей и границ решения задачи коммивояжера
- •8.1 Ветвление и оценка
- •8.2 Схема метода ветвей и границ решения задачи коммивояжера
- •8.3 Примеры решения задачи коммивояжера
- •8.4 Задания для самостоятельной работы
- •9 Метод ветвей и границ решения задачи о кратчайшем пути
- •9.1. Отношение доминирования
- •9.2 Задачи для самостоятельной работы
- •Список литературы
5 Схема метода ветвей и границ
Введем
обозначение:
![]() – текущий список подмножества множества
– текущий список подмножества множества![]() .
.
ШАГ
0.
Анализ
множества
![]() .
.
Вычислить
оценку
![]() .
Пусть
.
Пусть![]() – множество допустимых решений, которые
получены при оценивании множества
– множество допустимых решений, которые
получены при оценивании множества
![]() .
.
Если
![]() ,
то считаем, что
,
то считаем, что![]() ,
,![]() .
.
Если
![]() и для наилучшего из этих решений
и для наилучшего из этих решений![]() выполняется равенство
выполняется равенство
|
|
(5) |
тогда
![]() – решение задачи, КОНЕЦ.
– решение задачи, КОНЕЦ.
Если
равенство (5) не выполняется, тогда
считаем, что![]() .
.
ШАГ 1. Анализ списка.
Если
список
![]() не пустой, тогда перейти на ШАГ 2, иначе
- остановить вычисления. При этом:
не пустой, тогда перейти на ШАГ 2, иначе
- остановить вычисления. При этом:
если
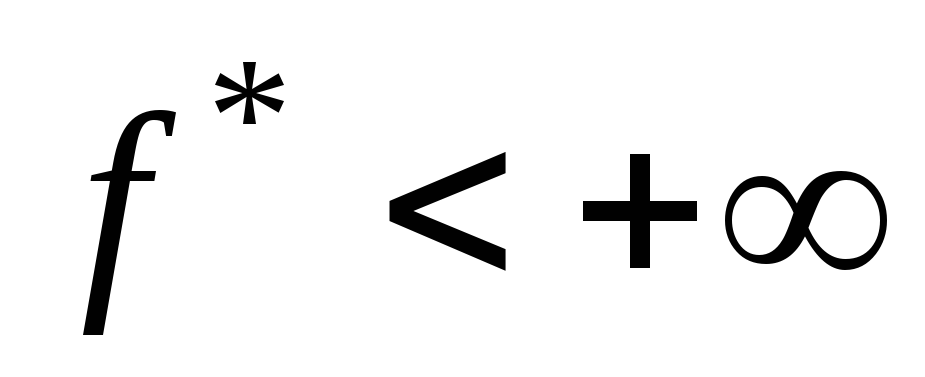 ,
тогда
,
тогда – значение начальной задачи, а
соответствующее рекорду решение –
решение задачи;
– значение начальной задачи, а
соответствующее рекорду решение –
решение задачи;если
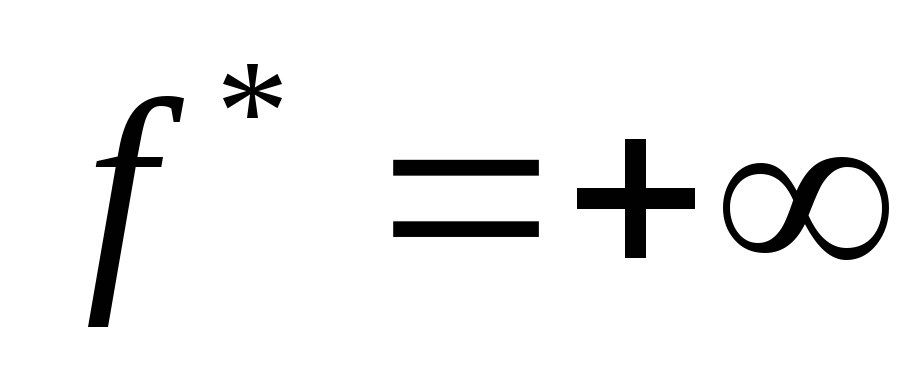 ,
тогда начальная задача не имеет
допустимых решений.
,
тогда начальная задача не имеет
допустимых решений.
ШАГ 2. Выбор множества для ветвления.
Выбрать
из списка
![]() множество
множество![]() согласно правилу:
согласно правилу:
![]() .
.
ШАГ 3. Ветвление.
Получить
множество
![]() ,.
,.![]() .
.
ШАГ 4. Анализ потомков.
Вычислить
оценку каждого элемента из
![]() .
.
ШАГ 5. Корректировка рекорда.
При
оценивании множеств
![]() допустимые решения начальной задачи
могли стать известными. Пусть
допустимые решения начальной задачи
могли стать известными. Пусть![]() – такое множество допустимых решений.
– такое множество допустимых решений.
Если
![]()
, тогда
, тогда
![]() .
.
ШАГ 6. Тест.
Сформировать новый список по правилу:
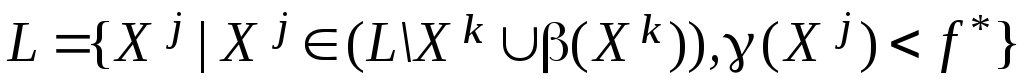 .
.
(при
этом с учетом того, что рекорд мог
измениться, из списка будут исключены
все подмножества
![]() ,
оценка которых хуже, чем у рекорда).
Переход на ШАГ 1.
,
оценка которых хуже, чем у рекорда).
Переход на ШАГ 1.
6 Стратегия
Под стратегией метода ветвей и границ для конкретной задачи понимают следующую совокупность правил и процедур.
Правило
ветвления
![]() .
.
Процедура вычисления оценок (нижних границ). При этом часто существует выбор между оценками, которые являются относительно точными, но трудоемкими (требуют много времени для вычислений), и оценками, которые являются не такими точными, но которые можно вычислить значительно быстрее. Правило выбора множества для ветвления. Обычно используются такие алгоритмы выбора множества:
выбор множества с наименьшей нижней оценкой;
выбор согласно правилу LIFO - "последним пришел - первым вышел";
выбор согласно правилу FIFO - "первым пришел - первым ушел";
ветвление в глубину.
Эффективность использования метода зависит от разработки стратегии для каждой конкретной задачи.
7 Метод ветвей и границ для решения задачи целочисленного линейного программирования
Рассмотрим задачу целочисленного линейного программирования (ЗЦЛП):
|
|
(6) |
|
|
(7) |
|
|
(8) |
|
|
(9) |
Разработаем стратегию метода ветвей и границ для решения данной задачи, то есть определим:
правило ветвления;
способ оценивания получаемых подмножеств;
правило выбора множества для ветвления;
тест.
Выберем
множества
![]() и
и![]() таким образом:
таким образом:
![]() –множество,
которое задается ограничениями (7)-(9) –
это множество изолированных точек,
которое показано на рисунке 7.1.
–множество,
которое задается ограничениями (7)-(9) –
это множество изолированных точек,
которое показано на рисунке 7.1.
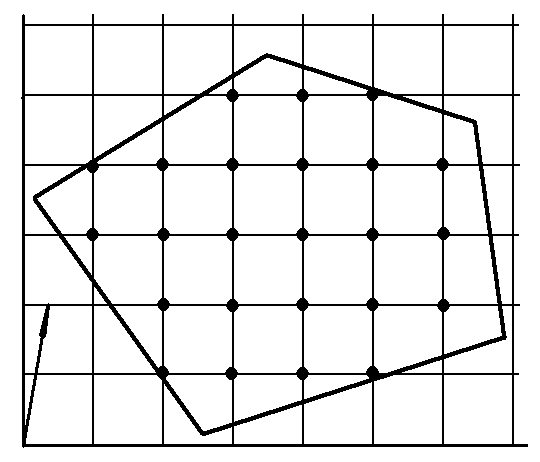
Рисунок 7.1 – Множество изолированных точек
![]() –множество,
которое задается ограничениями (7)-(8) –
это многогранное выпуклое множество,
которое показано на рисунке 7.2.
–множество,
которое задается ограничениями (7)-(8) –
это многогранное выпуклое множество,
которое показано на рисунке 7.2.
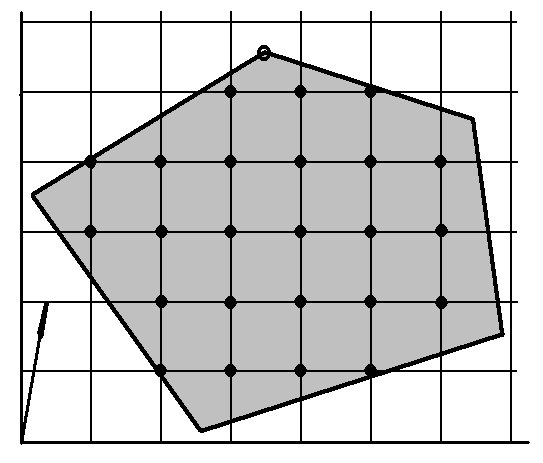
Рисунок 7.2 – Многогранное выпуклое множество
Согласно общей идее сначала решается задача с ослабленными ограничениями, то есть задача
![]()
Пусть
получили некоторое решение
![]() этой задачи. Если оно удовлетворяет
условиям (9), то исходная задача (6)-(9)
решена, если же нет, то значения
этой задачи. Если оно удовлетворяет
условиям (9), то исходная задача (6)-(9)
решена, если же нет, то значения![]() являются нижней гранью (оценкой)
оптимальности целевой функции задачи
(6)-(9).
являются нижней гранью (оценкой)
оптимальности целевой функции задачи
(6)-(9).
