
- •Теоретична механіка
- •Частина перша
- •1. Статика
- •1.1. Предмет статики. Основні визначення і поняття
- •1.2. Аксіоми статики (принципи статики)
- •1.3. В’язі і їхні реакції
- •1.4. Найпростіші теореми статики
- •1.6. Методичні вказівки для розв’язання задач про рівновагу
- •Статично означені й статично неозначені системи
- •Запитання для самоконтролю
- •2. Момент сили відносно центра та осі. Момент пари сил
- •2.1. Момент сили. Векторний і алгебраїчний моменти сили
- •Відносно центра
- •2.2. Момент сили відносно осі
- •Перший метод. Для знаходженняпроектуємо силуна площину.
- •2.3. Момент пари сил (рис. 2.9)
- •Запитання для самоконтролю
- •3. Довільна просторова система сил і умова її рівноваги
- •3.1. Основна теорема статики. Головний вектор і головний момент системи сил
- •3.2. Умови рівноваги довільної просторової системи сил
- •3.3. Умови рівноваги просторової системи паралельних сил
- •3.4. Умови рівноваги довільної плоскої системи сил
- •3.5. Рівновага системи тіл
- •Для їх визначення конструкцію розчленують, розрізають по шарніру на окремі тверді тіла і розглядають рівновагу кожного з них окремо.
- •3.6. Методика розв’язання задач з визначення реакцій в’язів складеної конструкції
- •Рівновага при наявності сил тертя
- •Запитання для самоконтролю
- •3.8. Ферми. Способи визначення зусиль у стержнях ферми
- •Запитання для самоконтролю
- •3.9. Центр паралельних сил і центр ваги
- •Запитання для самоконтролю
- •3.10. Завдання для контрольних робіт з розділу “Статика”
Запитання для самоконтролю
Які конструкції називають фермами?
Які припущення застосовують при розрахунках ферм у теоретичній механіці?
У чому полягає сутність методу вирізання вузлів при розрахунку зусиль у стержнях ферми?
Чи потрібно визначати реакції опор при розрахунку зусиль у стержнях ферми?
У чому полягає ідея методу Ріттера розрахунку ферм?
3.9. Центр паралельних сил і центр ваги
Центром
паралельних сил
називається точка на лінії дії рівнодійної
![]() цих сил, яка не змінює свого положення
при повороті всіх сил навколо точок їх
прикладення
цих сил, яка не змінює свого положення
при повороті всіх сил навколо точок їх
прикладення![]() на один і той самий кут в одному напрямку,
наприклад
на один і той самий кут в одному напрямку,
наприклад![]() (рис. 3.20).
(рис. 3.20).
|
Рис. 3.20 |
Якщо
головний вектор системи паралельних
сил
|
або в проекціях на координатні осі:
 ;
;
 ;
; ,
,
де
![]() - модуль її сили;
- модуль її сили;![]() - координати її точки прикладення.
- координати її точки прикладення.
Положення центра паралельних сил не залежить від напряму сил, а залежить тільки від їхніх модулів і їхніх точок прикладення.
Центром
ваги тіла
![]() називається центр паралельних сил ваги
його елементарних частин (рис. 3.21). Якщо
тіло можна поділити на деяку кількість
частин, в яких положення центра ваги
відоме, то координати центра ваги тіла
будуть:
називається центр паралельних сил ваги
його елементарних частин (рис. 3.21). Якщо
тіло можна поділити на деяку кількість
частин, в яких положення центра ваги
відоме, то координати центра ваги тіла
будуть:
|
Рис. 3.21 |
|
де
![]() - вага окремої частини;
- вага окремої частини;![]() - кількість частин;
- кількість частин;![]() - координати центра ваги окремої частини.
- координати центра ваги окремої частини.
Ці вирази визначають центр ваги неоднорідного тіла.
Центр ваги однорідного твердого тіла (або центр об’єму тіла) визначається за формулами
 ;
;
 ;
;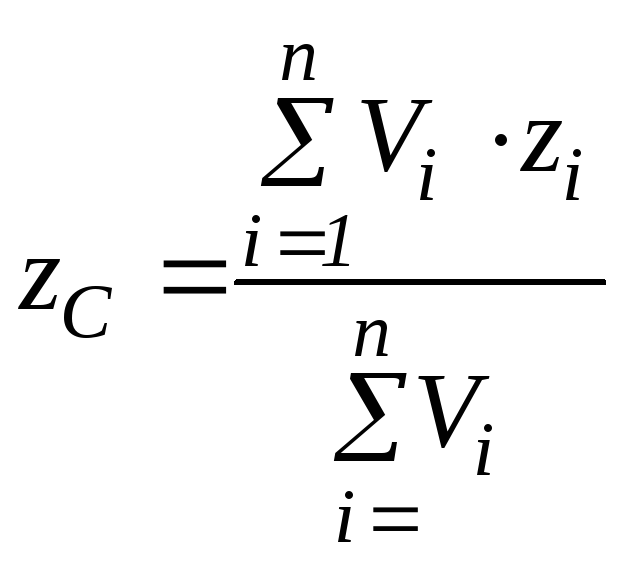 ,
,
де
 ,
,![]() - щільність, вага одиниці об’єму.
- щільність, вага одиниці об’єму.
Чисельники
мають назву статичних
моментів об’єму
відносно координатних площин
![]() .
У разі, якщо паралельні сили неперервно
розподілені по деякій однорідній (
.
У разі, якщо паралельні сили неперервно
розподілені по деякій однорідній (![]() )
площині
)
площині![]() ,
то вага частини
,
то вага частини![]() пропорційна їх площам
пропорційна їх площам![]() (рис. 3.22).
(рис. 3.22).
|
Рис. 3.22 |
У цьому випадку координати центра ваги площини визначаються за формулами
|
Вирази
![]() називаютьсястатичними
моментами площі плоскої фігури
відносно координатних осей
називаютьсястатичними
моментами площі плоскої фігури
відносно координатних осей
![]() і
і![]() (рис. 3.22).
(рис. 3.22).
Центр ваги лінії.
Якщо
однорідне тіло має форму тонкого
криволінійного стержня з постійною
площею
![]() поперечного перерізу, то вага частини
поперечного перерізу, то вага частини![]() пропорційна її довжині
пропорційна її довжині![]() .
Тоді координати центра ваги стержня
визначаються формулами
.
Тоді координати центра ваги стержня
визначаються формулами
 ;
;
 ;
; .
.
Чисельники
є статичними
моментами лінії
відносно координатних площин
![]() .
.
Методи визначення координат центра ваги однорідних тіл
1) Метод симетрії – якщо тіло має площину, вісь або центр симетрії, то його центр ваги лежить відповідно у площині, на осі або в центрі симетрії.
Приклади:
|
|
а)
стержень: центр ваги
|
|
|
б)
прямокутник: центр ваги
|
|
|
c)
трикутник (рис. 3.23,с): центр ваги
|
|
|
d)
коловий сектор (рис. 3.23,d): центр ваги
Півколо
( |
|
Рис. 3.23 |
де
кут
|
2) Метод розбивання. Якщо тіло (або площину) можна розбити на скінчене число елементарний фігур, в яких положення центра ваги відоме, то координати центра ваги визначаються формулами, доведеними вище.
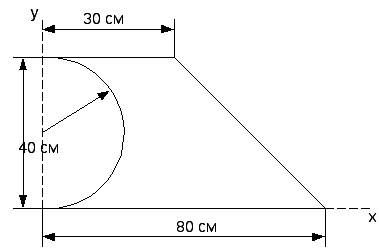
Приклад. Визначити координати центра ваги площі фігури (рис. 3.24,а).
|
|
Розв’язання. Розіб’ємо фігуру на три елементарні фігури, для яких відомі центри ваги, та легко визначаються площі: прямокутник, трикутник і півколо (рис. 3.24,б). Площу півкола, вирізану з прямокутника, вважаємо тілом з від’ємною площиною. Координати центра ваги плоскої фігури визначаємо за формулами
|
|
Рис. 3.24 |
де
![]() ,
,![]() - статичні моменти фігури відносно
координатних осей
- статичні моменти фігури відносно
координатних осей![]() і
і![]() ,
,![]() - площа фігури.
- площа фігури.
Дані про площі елементарних фігур (прямокутника, трикутника та півкола), координати їхніх центрів ваги, статичних моментів відносно координатних осей запишемо в таблиці.
|
|
|
|
|
|
|
|
1 |
1200 |
15,0 |
20,0 |
18000 |
24000 |
|
2 |
1000 |
46,7 |
13,3 |
46700 |
13300 |
|
3 |
-628 |
8,5 |
20,0 |
-5338 |
-12500 |
|
|
1572 |
‑ |
‑ |
59362 |
24700 |
Координати центра ваги всієї фігури:
![]() ;
;
![]() .
.
Центр
ваги
![]() площі всієї фігури показуємо на рисунку.
площі всієї фігури показуємо на рисунку.


 ,
,
 ;
;
 ;
; ,
,
 ;
; .
. а
а б
б c
c d
d .
. ,
координата точки
,
координата точки k
k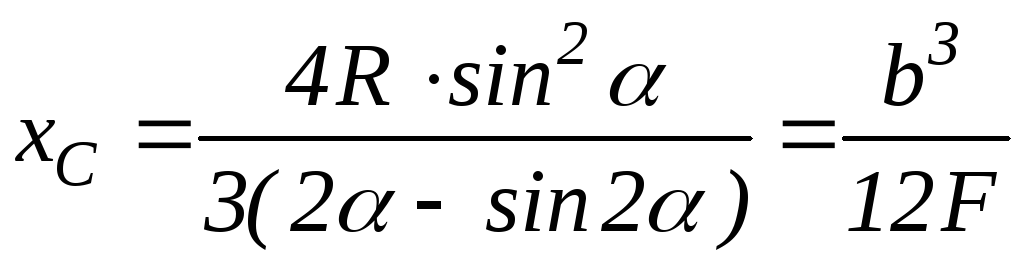 ,
, а
а б
б