lab_3_TS_Fall_2014
.docМіністерство освіти і науки України
Національний технічний університет України
“Київський політехнічний інститут”
Кафедра фізичної та біомедичної електроніки
лабораторна РОБОТА № 3
з дисципліни «Теорія сигналів»
|
«Моделювання лінійних систем в часовій та частотній області» |
Студента 3 курсу групи ДП-22
Мазура К.С.
Кількість балів: ______
Дата: ___________ 2014 р.
Київ – 2014
Мета роботи: дослідити роботу лінійних систем обробки дискретних сигналів; набути навичок моделювання лінійних стаціонарних дискретних систем в MatLAB.
Основні теоретичні відомості
Математичне моделювання обробки сигналів лінійною дискретною системою (ЛДС) включає в себе:
– розрахунок характеристик ЛДС в часовій області, z-області, та частотній області;
– розрахунок реакції ЛДС на вхідний сигнал по різницевому рівнянню;
– аналіз вхідних сигналів та реакцій ЛДС в часовій та частотних областях.
В MatLAB математичною моделлю ЛДС називають співвідношення між входом та виходом у вигляді різницевого рівняння або системи рівнянь, які дозволяють розрахувати реакцію системи на заданий вхідний вплив.
В часовій
області
основною характеристикою ЛДС є імпульсна
характеристика
,
а моделювання роботи ЛДС (розрахунок
реакції) виконується з використанням
одного з таких співвідношень між входом
та виходом:
1. Різницевого рівняння
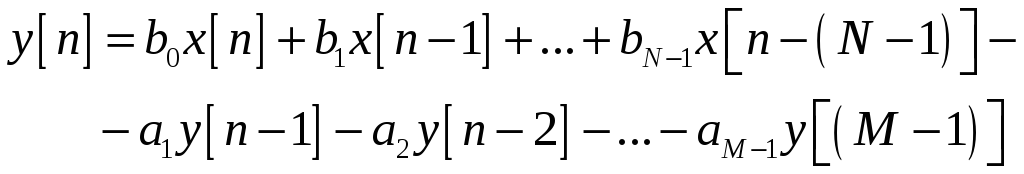
яке задається
векторами коефіцієнтів
та
.
В MatLAB всі функції аналізу систем
побудовані для випадку, коли перший
елемент вектору коефіцієнтів а
дорівнює одиниці:
.
2. Формули згортки
3. Системи рівнянь змінних стану.
В z-області основною характеристикою ЛДС є характеристична (схемна) функція:
,
яка, подібно до різницевого рівняння, задається векторами коефіцієнтів b та a та може мати різні вигляди математичного запису.
В частотній області основною характеристикою ЛДС є комплексна частотна характеристика, а також її модуль (амплітудно-частотна характеристика, АЧХ) та аргумент (фазо-частотна характеристика, ФЧХ):
.
Порядок роботи
Моделювання роботи ЛДС з використанням різницевого рівняння.
1. На основі власної дати народження записати різницеве рівняння:
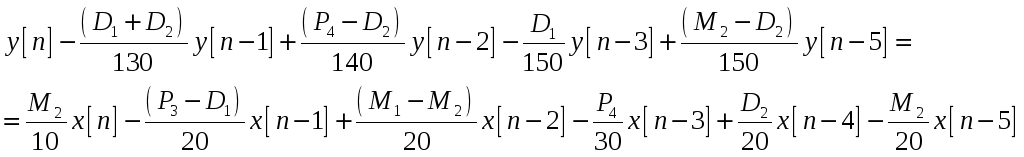
Дата народження: 06.11.1995 В програмі задати вектори a та b коефіцієнтів рекурсивної та нерекурсивної частини ЛДС.
2. Сформувати відліки синусоїдального сигналу частоти 10 Гц тривалістю 1 сек. амплітуди 1 В, дискретизованого з частотою 256 Гц. Розрахувати реакцію системи на отриманий сигнал (функція filter) для двох випадків:
2.1. нульові початкові умови;
2.2. випадкові початкові умови (скористатися функцією rand).
Побудувати графіки вхідного та вихідного сигналів в одному вікні, позначивши точки графіку, що відповідають відлікам, та огинаючі графіків (налаштувати функцію plot). Побудувати в окремому вікні перші 100 мс вхідного та вихідного сигналу. Зробити висновки щодо вигляду вихідного сигналу відносно вхідного (форма, амплітуда, спотворення, підсилення).
clc
clear all
close all
a=[1 -0.0462 -0.0071 0 0 -0.0333];
b=[0.6 -0.45 0 -0.1667 0.3 -0.05];
Fs=256;
T=1;
t=0:1/Fs:T;
len=max(length(a),length(b))-1;
is=sin(2*pi*10*t);
os = filter(b,a,is);
osr = filter(b,a,is,rand(1,len));
figure
plot(t,is,'.-',t,os,'.-',t,osr,'.-');
grid on;
xlim ([0 0.1]);
ylim ([-1.5 1.5]);
legend('<Вхідний сигнал>', '<Вихідний сигнал без запізнення>','<Вихідний сигнал із запізненням>')
xlabel('t,c');
ylabel('A,B');
figure
plot(t,is,'.-',t,os,'.-',t,osr,'.-');
grid on;
ylim ([-1.5 1.5]);
legend('<Вхідний сигнал>', '<Вихідний сигнал без запізнення>','<Вихідний сигнал із запізненням>')
xlabel('t,c');
ylabel('A,B');
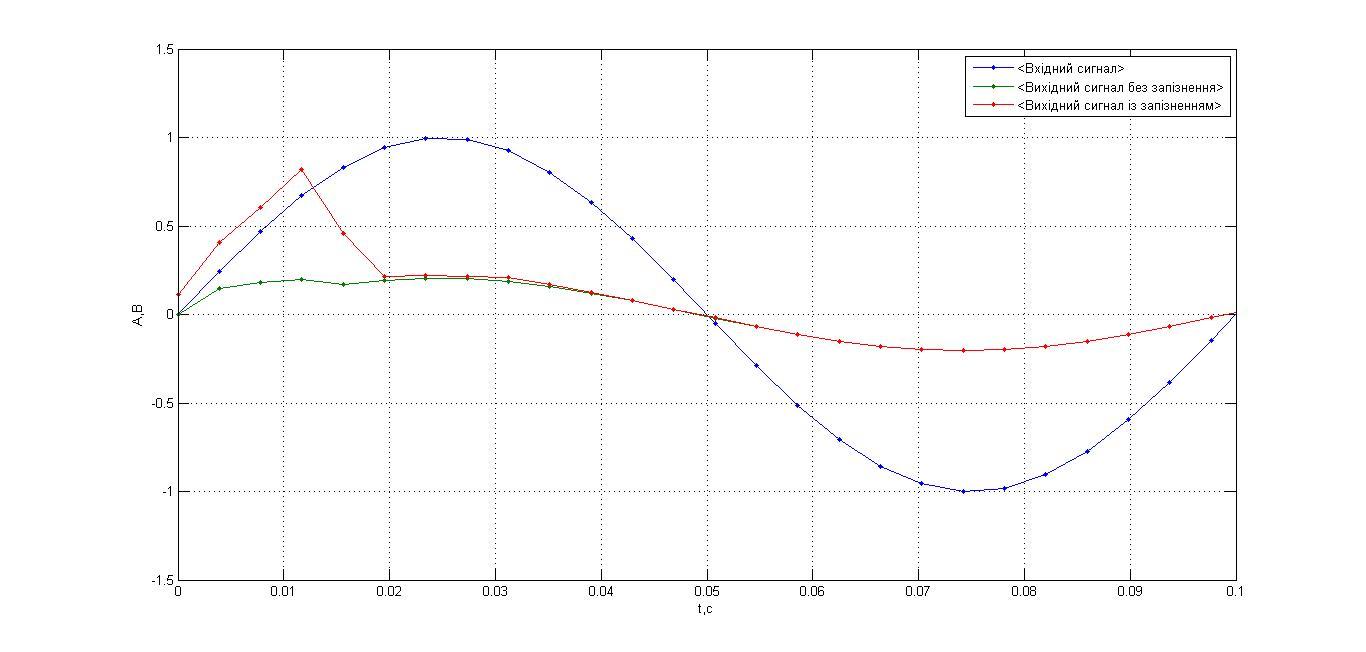
Висновок: вхідний та вихідний сигнал – синусоїдальні, мають однаковий період, проте вихідний сигнал має спотворення на початку. Вихідні сигнали (з запізненням та без) різняться лише протягом перших 40 мс, далі вони співпадають. Вхідний сигнал послаблюється. Різниця фаз майже непомітна (найімовірніше, вона становить лише декілька градусів).
3. Написати програму для визначення коефіцієнту передачі напруги ЛДС на частоті 10 Гц, а також різницю фаз між вихідним і вхідним сигналом.
clc
clear all
close all
a=[1 -0.0462 -0.0071 0 0 -0.0333];
b=[0.6 -0.45 0 -0.1667 0.3 -0.05];
Fs=256;
T=1;
t=0:1/Fs:T;
len=max(length(a),length(b))-1;
is=sin(2*pi*10*t);
os = filter(b,a,is);
osr = filter(b,a,is,rand(1,len));
[is_max, N]=findpeaks(abs(is));
[os_max, N1]=findpeaks(abs(os));
delta_t=t(N(7))-t(N1(7));
K_u = os_max(7)/is_max(7);
disp(['Різниця фаз ',num2str(delta_t)]);
disp(['Коефіціент підсилення ',num2str(K_u)])
Різниця фаз 0.050781
Коефіціент підсилення 0.20318
4. Сформувати два синусоїдальних сигнали частоти 3 та 20 Гц тривалістю 1 с. Проілюструвати властивість адитивності системи, визначивши реакцію системи спочатку на кожний з сигналів окремо, а потім на суму цих сигналів. Проілюструвати властивість однорідності системи. Навести необхідні графіки.
clc
clear all
close all
a=[1 -0.0462 -0.0071 0 0 -0.0333];
b=[0.6 -0.45 0 -0.1667 0.3 -0.05];
Fs=256;
T=1;
t=0:1/Fs:T;
is1=sin(2*pi*3*t);
is2=sin(2*pi*20*t);
os1=filter(b,a,is1);
os2=filter(b,a,is2);
os3=filter(b,a,is1 + is2);
os4=filter(b,a,is1*3);
os5=3*filter(b,a,is1);
subplot(2,1,1);
plot (t,os3);
xlabel('t,c');
ylabel('А,B');
title('Реакція ЛДС на суму двох сигналів');
subplot(2,1,2);
plot (t,os1+os2);
xlabel('t,c');
ylabel('А,B');
title('Сума реакцій ЛДС на два сигнали');
figure
subplot(3,1,1);
plot (t,os1);
xlabel('t,c');
ylabel('А,B');
title('Вхідний сигнал');
subplot(3,1,2);
plot (t,os4);
xlabel('t,c');
ylabel('А,B');
title('Реакція ЛДС на сигнал втричі більшої амплітуди ');
subplot(3,1,3);
plot(t,os5);
xlabel('t,c');
ylabel('А,B');
title('Реакція системи на сигнал, помножена на три');
5. Розрахувати за допомогою функції filter перші 30 відліків імпульсної характеристики системи, подавши на вхід системи одиничний імпульс (при нульових початкових умовах). Побудувати графіки вхідного та вихідного сигналу (функція stem).
clc
clear all
close all
a=[1 -0.0462 -0.0071 0 0 -0.0333];
b=[0.6 -0.45 0 -0.1667 0.3 -0.05];
t=0:29;
imp=zeros(1,30);
imp(1,1)=1;
os=filter(b,a,imp);
subplot(2,1,1);
stem (t,imp);
xlabel('n');
ylabel('А,B');
title('Вхідний сигнал (одиничний імпульс)');
subplot(2,1,2);
stem (t,os);
xlabel('n');
ylabel('А,B');
title('Вихідний сигнал (імпульсна харктеристика)');
6. Розрахувати 30 відліків імпульсної характеристики системи по коефіцієнтам різницевих рівнянь з використанням функції impz. Порівняти результати з результатами п. 5, побудувати графіки, зробити висновки.
clc
clear all
close all
a=[1 -0.0462 -0.0071 0 0 -0.0333];
b=[0.6 -0.45 0 -0.1667 0.3 -0.05];
imp=impz(b,a,30);
stem (imp);
xlabel('n');
ylabel('А,B');
title('Вихідний сигнал (імпульсна харктеристика)');
Імпульсні характеристики, знайдені в пунктах 5 і 6 співпадають, з чого можна зробити висновки, що ми можемо знаходити імпульсну характеристику двома способами.
Моделювання роботи ЛДС з використанням рівняння згортки.
7. Розрахувати реакцію системи на сигнал з п. 2 з використанням функції розрахунку згортки conv. Побудувати графіки вхідного та вихідного сигналу, аналогічні п. 2 (з нульовими початковими умовами). Порівняти з результатами виконання п. 2. Зробити висновки
clc
clear all
close all
a=[1 -0.0462 -0.0071 0 0 -0.0333];
b=[0.6 -0.45 0 -0.1667 0.3 -0.05];
Fs=256;
T=1;
t=0:1/Fs:T;
len=max(length(a),length(b))-1;
is=sin(2*pi*10*t);
h=impz(b,a);
os=conv(is,h);
t1=0:1/Fs:1/Fs*(length(os)-1);
plot(t,is,'.-',t1,os,'.-');
grid on;
xlim ([0 1.1]);
ylim ([-1.5 1.5]);
legend('<Вхідний сигнал>', '<Вихідний сигнал >')
xlabel('t,c');
ylabel('A,B');
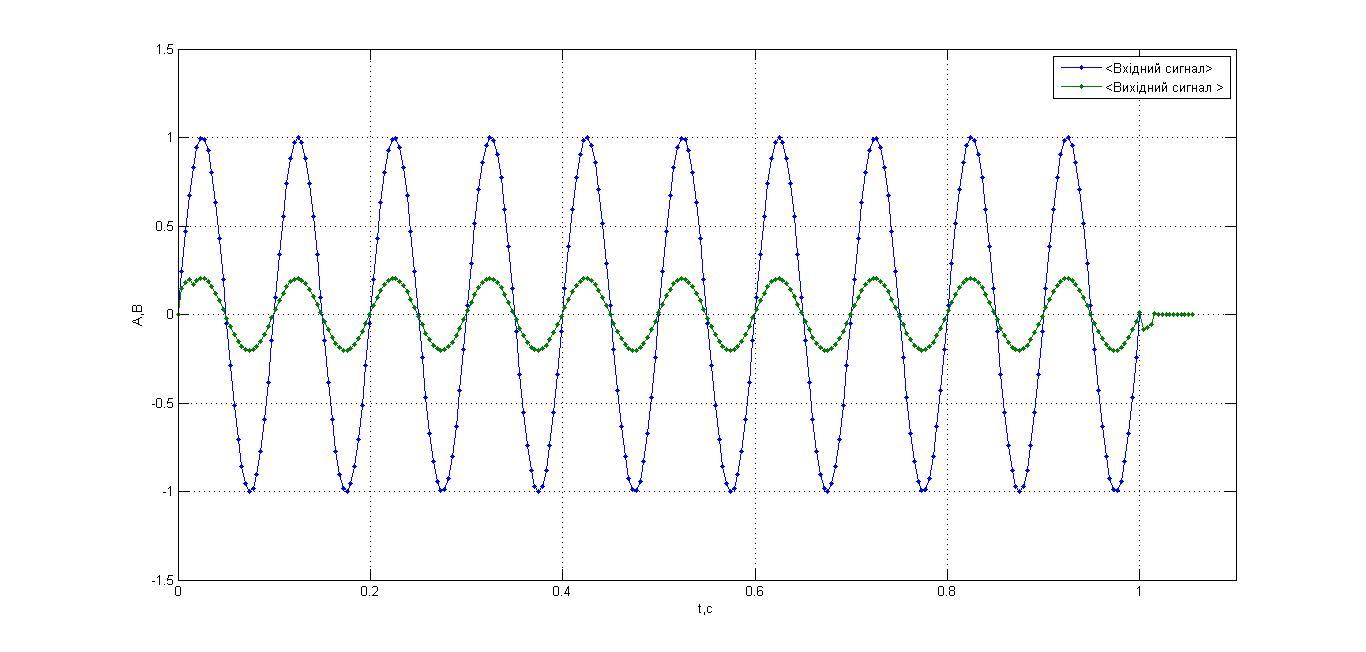
Висновок: результати виконання програм пунктів 2 і 7 співпадають, але в п.7 ми бачимо, що програма продовжувала рахувати реакцію системи навіть тоді, коли сигнал уже закінчився. Щоб не було цього неіснуючого «хвоста» слід доповнити вхідний сигнал нульовими відліками.
Моделювання роботи ЛДС в частотній області.
9. Обчислити комплексну частотну характеристику системи з використанням функції freqz, побудувати з її допомогою графіки АЧХ та ФЧХ. Розрахувати 100 значень КЧХ для частоти дискретизації 256 Гц. Зробити висновки щодо величини коефіцієнта передачі системи на різних частотах. Визначити проміжки частот, на яких система підсилює сигнал (записати у висновках). Візуально пересвідчитись в правильності визначення коефіціенту передачі і фазового зміщення, які розраховані в п. 3.
clc
clear all
close all
a=[1 -0.0462 -0.0071 0 0 -0.0333];
b=[0.6 -0.45 0 -0.1667 0.3 -0.05];
Fs=256;
[H,f]=freqz(b,a,1000,Fs);
q=f(abs(H)<=1);
ans=['система послаблює сигнал при частоті від ',num2str(q(1)),' Гц до ',num2str(q(end)),' Гц']
freqz(b,a,100,Fs);
title ('АЧХ та ФЧХ при частоті дискретизації Fs=256 Гц');
система послаблює сигнал при частоті від 0 Гц до 105.728 Гц
Висновок: коефіцієнт передачі системи має значення менше одиниці (ЛДС послаблює сигнал) на частотах 0 .. 105.728 Гц, проте ЛДС послаблює його на цьому проміжку нерівномірно. Потім вона починає посилювати його.
10. Розрахувати АЧХ та ФЧХ системи по обчисленій в п. 9 комплексній частотній характеристиці з використанням функцій abs та phase. Побудувати графіки, порівняти з графіками, отриманими в п. 9. Зробити висновки щодо характеру зміни модуля коефіцієнта передачі системи з частотою.
clc
clear all
close all
a=[1 -0.0462 -0.0071 0 0 -0.0333];
b=[0.6 -0.45 0 -0.1667 0.3 -0.05];
Fs=256;
T=1;
t=0:1/Fs:T;
[H,w]=freqz(b,a,100,Fs);
Ku=abs(H);
Fi=phase(H);
subplot(2,1,1)
plot(w,Ku);
xlim([0, 130])
xlabel('f,Hz');
ylabel('Ku');
title('AЧХ');
grid on
subplot(2,1,2)
plot(w,Fi)
xlim([0, 130])
xlabel('f,Hz');
ylabel('fi, rad');
title('ФЧХ');
grid on
Результати збігаються з п.9
11. Побудувати функцію, яка визначає значення АЧХ та ФЧХ системи на довільній частоті. Перевірити за допомогою отриманої функції правильність розрахунків з п. 3.
function [K_u fi]=lab_3_11(f)
if (f>=0)
n=10000;
Fs=256;
a=[1 -0.0462 -0.0071 0 0 -0.0333];
b=[0.6 -0.45 0 -0.1667 0.3 -0.05];
[h,f1]=freqz(b,a,n,Fs);
N=round(f/f1(2))+1;
K_u=abs(h(N));
fi=phase(h(N));
else
disp('err');
end
K_u = 0.2032
fi = 0.0504
Результати співпадають зі значеннями п.3
12. Розрахувати реакцію ЛДС на послідовність прямокутних імпульсів зі шпаруватістю 30 % (функція square). Побудувати графіки вхідного та вихідного сигналів, зробити висновки щодо спотворення вихідного сигналу відносно вхідного.
clc;
clear all;
close all;
a=[1 -0.0462 -0.0071 0 0 -0.0333];
b=[0.6 -0.45 0 -0.1667 0.3 -0.05];
Fs=256;
t=0:1/Fs:1;
is=square(2*pi*t*3,30);
os=filter(b,a,is);
plot(t,is,t,os);
xlim([0,1.1]);
ylim([-1.1,1.1]);
grid on;
xlabel('t,c');
ylabel('A,B');
title('Реакція системи на послідовність прямокутних імпульсів');
legend('Вхідний сигнал','Вихідний сигнал')
