
- •Т е о р і я й м о в і р н о с т е й т а
- •03056, Київ-56, просп. Перемоги, 37 Зміст
- •1. Елементи комбінаторики
- •2. Біноміальні тотожності
- •3. Формула включень та виключень
- •4. Класичне означення ймовірності
- •5. Геометричний метод знаходження ймовірності
- •6. Умовні ймовірності, незалежні події, формула повної ймовірності, формула Байєса
- •Дискретні випадкові величини, математичне сподівання та дисперсія
- •Загальне поняття випадкової величини, функції від випадкових величин
- •Граничні теореми
- •0.74 1.12 3.75 4.33 5.71 6.09 7.89 8.03 9.55 10.22.
- •Список використаної літератури
Дискретні випадкові величини, математичне сподівання та дисперсія
Випадкова величина
 називаєтьсядискретною,
якщо
вона може приймати лише скінченну або
зліченну кількість значень
називаєтьсядискретною,
якщо
вона може приймати лише скінченну або
зліченну кількість значень
 .Розподіл
дискретної
випадкової величини задається набором
ймовірностей
.Розподіл
дискретної
випадкової величини задається набором
ймовірностей
![]()
Математичне
сподівання
![]() дискретної випадкової величини
визначається таким чином. Припустимо,
що ряд
дискретної випадкової величини
визначається таким чином. Припустимо,
що ряд![]() збігається. Тоді
збігається. Тоді
![]() (23)
(23)
Якщо
ряд
![]() розбігається, то математичне сподівання
не існує.Дисперсія
дискретної випадкової величини
розбігається, то математичне сподівання
не існує.Дисперсія
дискретної випадкової величини
![]() визначається рівністю
визначається рівністю
![]() (24)
(24)
Нехай
![]() – дискретна випадкова величина, яка
приймає значення
– дискретна випадкова величина, яка
приймає значення![]() з ймовірністю
з ймовірністю![]() Сумісний
розподіл випадкових
величин
Сумісний
розподіл випадкових
величин
![]() та
та![]() задається набором ймовірностей
задається набором ймовірностей
![]()
Коваріація
![]() ікоефіцієнт
кореляції
ікоефіцієнт
кореляції
![]() випадкових величин
випадкових величин![]() і
і![]() визначаються формулами
визначаються формулами
![]()
![]() (25)
(25)
де
![]() ,
,![]() та
та![]() ,
,![]() обчислюються згідно з (23), (24).
обчислюються згідно з (23), (24).
Приклад
1.
Урна
містить
![]() куль, позначених номерами від 1 до
куль, позначених номерами від 1 до![]() .
Послідовно виймають
.
Послідовно виймають![]() куль, повертаючи кожен раз взяту кулю
назад. Нехай
куль, повертаючи кожен раз взяту кулю
назад. Нехай![]() – найбільший номер, який було одержано
при цьому. Знайти розподіл
– найбільший номер, який було одержано
при цьому. Знайти розподіл![]() та
та![]() .
.
Розв’язання.
Позначимо через
![]() номер кулі, яка була вийнята
номер кулі, яка була вийнята![]() -ю
за рахунком. Це дискретна випадкова
величина, яка дорівнює
-ю
за рахунком. Це дискретна випадкова
величина, яка дорівнює![]()
![]() з ймовірністю
з ймовірністю![]() .
Тоді
.
Тоді![]() .
Враховуючи незалежність випадкових
величин
.
Враховуючи незалежність випадкових
величин![]() ,
маємо
,
маємо
![]()
![]()
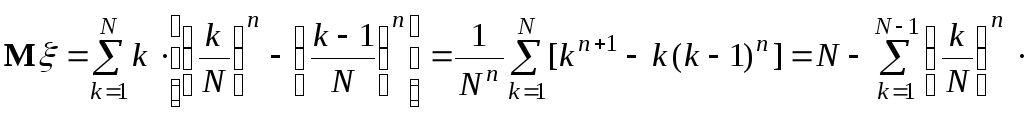
Приклад
2.
Підкидають
два гральні кубики. Описати простір
елементарних подій
![]() .
Нехай
.
Нехай![]() – кількість очок на першому кубику, а
– кількість очок на першому кубику, а![]() – максимальна кількість очок, що випали
на двох кубиках. Знайти сумісний розподіл
– максимальна кількість очок, що випали
на двох кубиках. Знайти сумісний розподіл![]() та
та![]() і обчислити
і обчислити![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() та
та![]()
Розв’язання.
Оскільки на кожному кубику може випасти
від одного до шести очок, то маємо
![]() Визначимо спочатку сумісний розподіл
випадкових величин
Визначимо спочатку сумісний розподіл
випадкових величин![]() та
та![]() .
Нехай
.
Нехай![]() Тоді
Тоді![]() якщо
якщо![]() ;
;![]() якщо
якщо![]() ;
;![]()
![]() Звідси отримуємо розподіли випадкових
величин
Звідси отримуємо розподіли випадкових
величин![]() та
та![]() :
:
![]()
![]()
Згідно з (23) та (24) обчислюємо математичні сподівання та дисперсії:
![]()
![]()
![]()
Коваріація
![]() ікоефіцієнт
кореляції
ікоефіцієнт
кореляції
![]() визначаються згідно з (25):
визначаються згідно з (25):
![]()
Біноміальний розподіл (розподіл Бернуллі). Проводяться
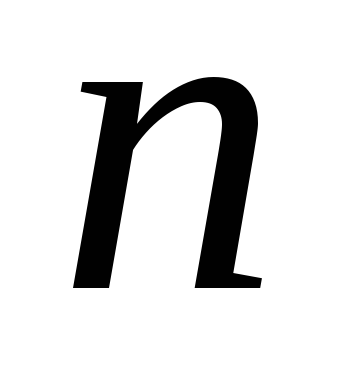 незалежних випробувань, результатами
яких може бути“успіх”
(з ймовірністю
незалежних випробувань, результатами
яких може бути“успіх”
(з ймовірністю
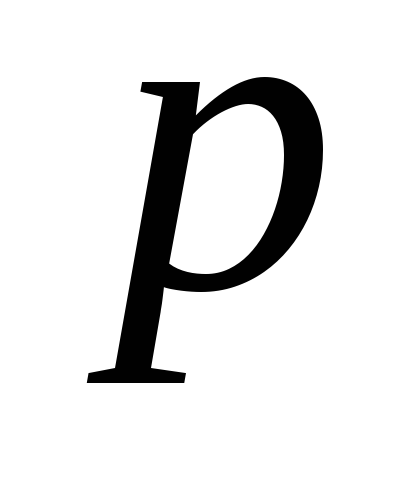 )
або“невдача”
(з ймовірністю
)
або“невдача”
(з ймовірністю
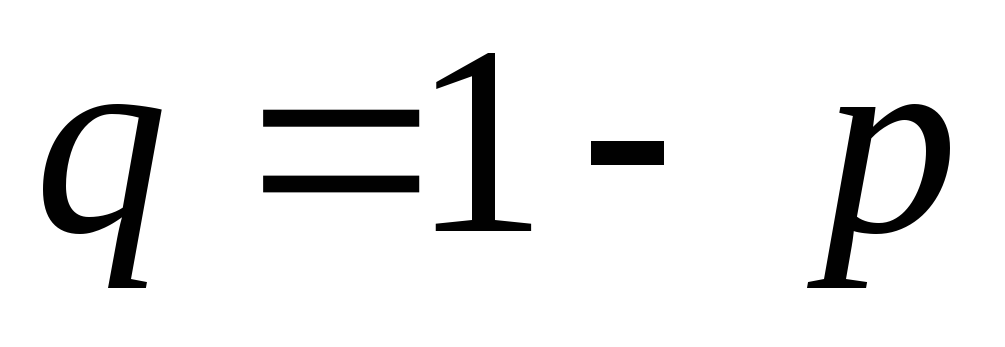 ).
Якщо через
).
Якщо через позначити кількість“успіхів”
у серії з
позначити кількість“успіхів”
у серії з
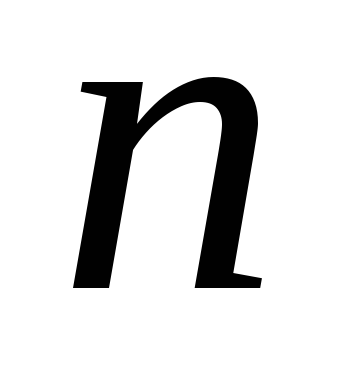 випробувань, то отримаємо біноміальний
розподіл
випробувань, то отримаємо біноміальний
розподіл
![]()
Приклад
3.
Що
більш імовірно, виграти у гравця, рівного
собі за силою гри: a)
3 партії з 4, чи 5 партій з 8; b)
не
менше 3 партій з 4, чи не менше 5 партій з
8; c)
не більше
![]() з
з![]() партій, чи більше
партій, чи більше![]() з
з![]() партій;d)
не більше
партій;d)
не більше
![]() з
з![]() партій, чи більше
партій, чи більше![]() з
з![]() партій?
партій?
Розв’язання.
Оскільки гравці є рівними за силою гри,
то ймовірність виграшу кожним з них
однієї партії дорівнює
![]() .
Тому ймовірність виграшу першим гравцем
.
Тому ймовірність виграшу першим гравцем![]() партій з
партій з![]() дорівнює
дорівнює![]() Позначимо через
Позначимо через![]() і
і![]() відповідно ймовірності першої та другої
подій у кожному з чотирьох вказаних
вище випадків.
відповідно ймовірності першої та другої
подій у кожному з чотирьох вказаних
вище випадків.
A.
![]() тобто
тобто
![]() – більш ймовірним є виграш 3 партій з
4.
– більш ймовірним є виграш 3 партій з
4.
B.
![]() тобто
тобто
![]() – більш ймовірним є виграш не менше 5
партій з 8.
– більш ймовірним є виграш не менше 5
партій з 8.
C.
![]() тобто більш ймовірним є виграш не більше
тобто більш ймовірним є виграш не більше
![]() з
з![]() партій.
партій.
D.
![]() тобто обидві події є рівноймовірними.
тобто обидві події є рівноймовірними.
Приклад
4.
Проводиться
експеримент, який полягає у серії
незалежних випробувань, результатом
кожного з яких може бути “успіх”
(з ймовірністю
![]() )
або“невдача”
(з ймовірністю
)
або“невдача”
(з ймовірністю
![]() ).
Експеримент може бути завершений лише
в момент чергового успіху. Якщо відбулось
).
Експеримент може бути завершений лише
в момент чергового успіху. Якщо відбулось![]() успіхів (
успіхів (![]() ),
то експеримент було успішно завершено
з ймовірністю
),
то експеримент було успішно завершено
з ймовірністю![]() .
Знайти середню кількість випробувань,
необхідних для завершення експерименту.
.
Знайти середню кількість випробувань,
необхідних для завершення експерименту.
Розв’язання.
Позначимо через
![]() кількість випробувань, що було здійснено
до завершення експерименту,
кількість випробувань, що було здійснено
до завершення експерименту,![]() – ймовірність того, що для завершення
експерименту знадобиться не більше
– ймовірність того, що для завершення
експерименту знадобиться не більше![]() випробувань (
випробувань (![]() ).
Нехай
).
Нехай![]() – ймовірність того, що серед
– ймовірність того, що серед![]() випробувань рівно
випробувань рівно![]() було успішних. Тоді за формулою повної
ймовірності маємо
було успішних. Тоді за формулою повної
ймовірності маємо
![]()
де
![]() (якщо
відомо, що серед
(якщо
відомо, що серед![]() випробувань
випробувань![]() були успішними, то експеримент завершиться
з ймовірністю
були успішними, то експеримент завершиться
з ймовірністю![]() ).
Підставляючи в цю формулу значення
).
Підставляючи в цю формулу значення![]() та
та![]() і враховуючи те, що
і враховуючи те, що![]() ,
отримуємо
,
отримуємо
![]()
![]()
Оскільки
![]() ,
маємо
,
маємо
![]()
Для обчислення останньої суми використаємо таку рівність
![]() (26)
(26)
Поклавши
![]() маємо
маємо
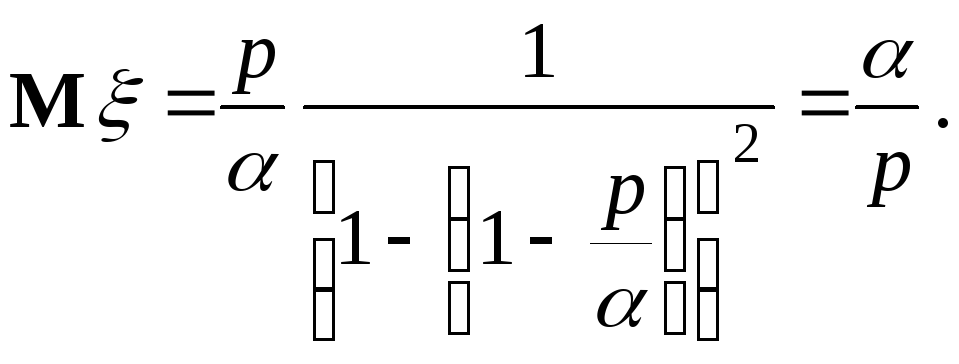
Геометричний розподіл. Проводиться серія незалежних випробувань, результатами яких може бути “успіх” (з ймовірністю
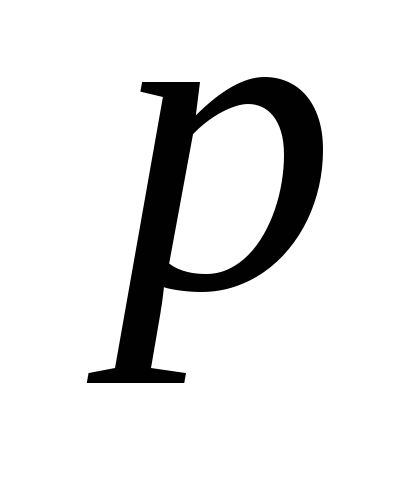 )
або “невдача” (з ймовірністю
)
або “невдача” (з ймовірністю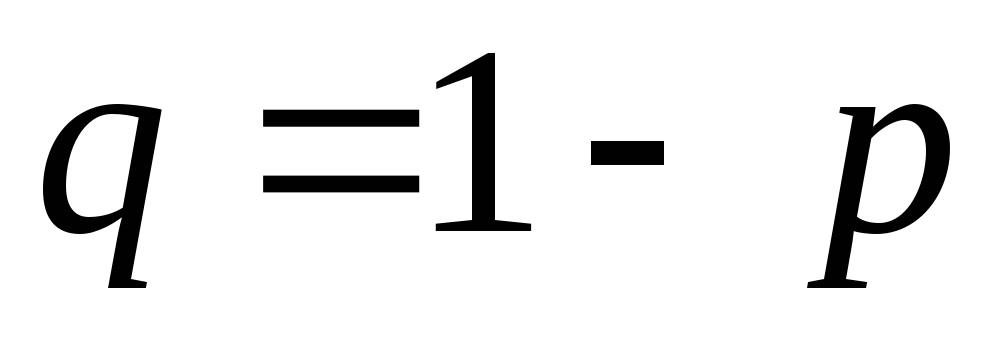 ).
Якщо через
).
Якщо через позначити кількість “невдач” до
першого“успіху”,
то отримаємо геометричний розподіл
позначити кількість “невдач” до
першого“успіху”,
то отримаємо геометричний розподіл
![]()
Приклад
5.
Два приятелі грають у гру, почергово
підкидаючи кубик. Виграє той, у кого
раніше з’явиться
шестірка. Знайти ймовірність того, що
гра закінчиться при
![]() -му
підкиданні кубика. Оцінити, наскільки
ймовірність виграти більше у того, хто
починав першим.
-му
підкиданні кубика. Оцінити, наскільки
ймовірність виграти більше у того, хто
починав першим.
Розв’язання.
Ймовірність отримати шестірку при
одному підкиданні дорівнює
![]() .
Тому гразакінчиться
при
.
Тому гразакінчиться
при
![]() -му
підкиданні з ймовірністю
-му
підкиданні з ймовірністю![]() Для того, щоб оцінити ймовірність
Для того, щоб оцінити ймовірність![]() виграшу у того, хто починав першим,
достатньо просумувати
виграшу у того, хто починав першим,
достатньо просумувати![]() по всіх непарних
по всіх непарних![]() ,
тобто
,
тобто
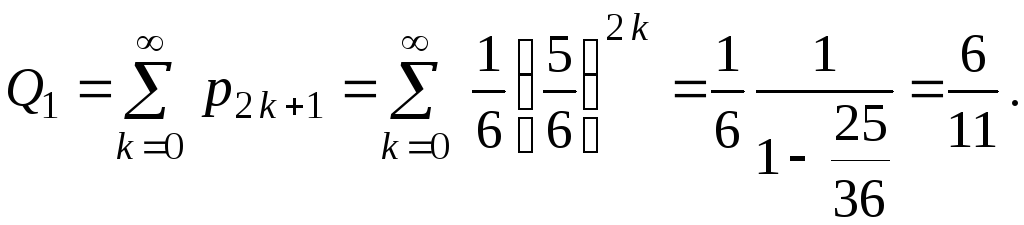
Аналогічно
![]() Тобто
Тобто![]()
Приклад
6.
Випадкові величини
![]() і
і![]() є незалежними і мають той самий
геометричний розподіл
є незалежними і мають той самий
геометричний розподіл![]() Нехай
Нехай
![]() Знайти розподіл величини
Знайти розподіл величини![]() і сумісний розподіл величин
і сумісний розподіл величин![]() і
і
![]() .
.
Розв’язання.
Сумісний розподіл величин
![]() і
і
![]() позначимо
позначимо
![]()
![]()
Очевидно,
що
![]() якщо
якщо![]() ;
;![]() якщо
якщо![]() ;
;![]() Звідси отримуємо розподіл випадкової
величини
Звідси отримуємо розподіл випадкової
величини![]() :
:
![]()
Розподіл Пуассона. Випадкова величина
 має розподіл Пуассона з параметром
має розподіл Пуассона з параметром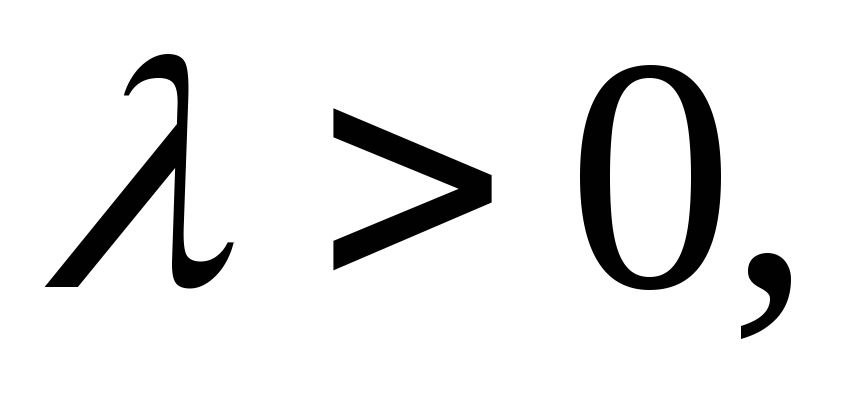 якщо вона приймає значення
якщо вона приймає значення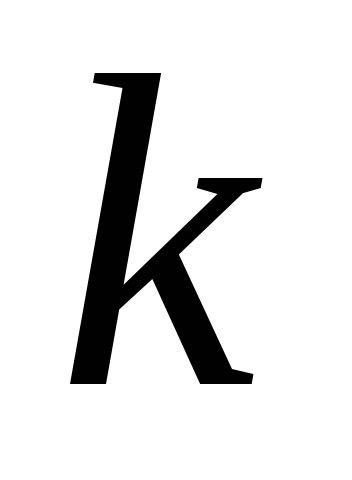 з ймовірністю
з ймовірністю
![]() (27)
(27)
Розглянемо
послідовність серій випробувань
Бернуллі. Припустимо, що в
![]() -й
серії здійснено
-й
серії здійснено![]() випробувань (так звана“трикутна
схема”),
причому ймовірність “успіху”
дорівнює
випробувань (так звана“трикутна
схема”),
причому ймовірність “успіху”
дорівнює
![]() .
Якщо через
.
Якщо через![]() позначити кількість“успіхів”
у серії з
позначити кількість“успіхів”
у серії з
![]() випробувань, то отримаємо біноміальний
розподіл
випробувань, то отримаємо біноміальний
розподіл
![]()
Теорема
Пуассона. Якщо
![]() при
при![]() ,
то для будь-якого фіксованого
,
то для будь-якого фіксованого![]()
![]() (28)
(28)
де
![]()
Співвідношення (28) дає можливість суттєво спростити обчислення біноміального розподілу у випадку великої кількості випробувань і малої ймовірності “успіху”:
![]() (29)
(29)
Приклад
7.
Випадкові величини
![]() та
та![]() є незалежними і мають розподіл Пуассона
з параметрами
є незалежними і мають розподіл Пуассона
з параметрами![]() та
та![]() відповідно. Знайти умовний розподіл
величини
відповідно. Знайти умовний розподіл
величини![]() при умові, що
при умові, що![]()
Розв’язання. Обчислимо спочатку
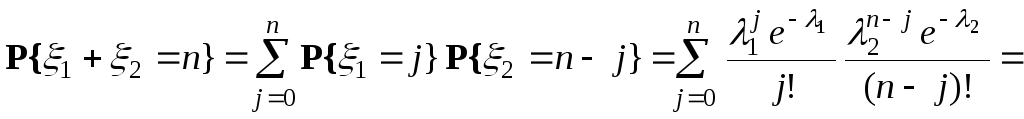
![]()
Використовуючи формулу для умовних ймовірностей, маємо
![]()
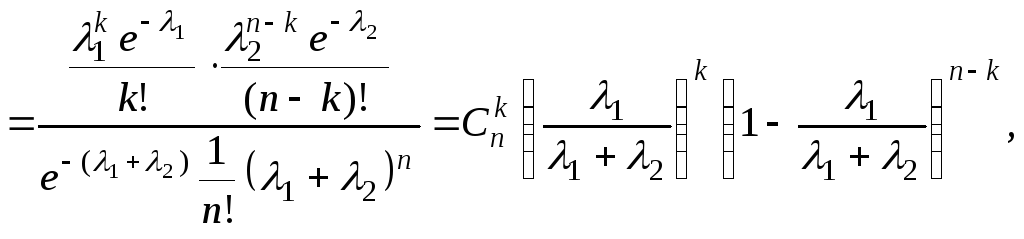
тобто
умовний розподіл величини
![]() при умові, що
при умові, що![]() є біноміальним розподілом з параметрами
є біноміальним розподілом з параметрами![]() та
та![]()
Приклад
8.
Підручник надруковано накладом 10 000
примірників. Імовірність того, що
підручник бракований, дорівнює 0.0001.
Знайти закон розподілу випадкової
величини
![]() – кількості бракованих підручників у
накладі. Визначити
– кількості бракованих підручників у
накладі. Визначити
![]() ,
,![]() та ймовірності того, що наклад містить:a)
два бракованих підручники; b)
щонайменше два бракованих підручники.
та ймовірності того, що наклад містить:a)
два бракованих підручники; b)
щонайменше два бракованих підручники.
Розв’язання.
Очевидно, що випадкова величина
![]() має розподіл Бернуллі з параметрами
має розподіл Бернуллі з параметрами![]() Це якраз той випадок, коли можна
застосувати теорему Пуассона і
скористатися наближеною рівністю (29):
Це якраз той випадок, коли можна
застосувати теорему Пуассона і
скористатися наближеною рівністю (29):
![]()
де
![]() Згідно з (27)
Згідно з (27)
![]() і
і![]() Ймовірність того, що у накладі наявні
два бракованих підручники дорівнює
Ймовірність того, що у накладі наявні
два бракованих підручники дорівнює
![]()
Ймовірність того, що у накладі є щонайменше два бракованих підручники дорівнює
![]()
