
- •Т е о р і я й м о в і р н о с т е й т а
- •03056, Київ-56, просп. Перемоги, 37 Зміст
- •1. Елементи комбінаторики
- •2. Біноміальні тотожності
- •3. Формула включень та виключень
- •4. Класичне означення ймовірності
- •5. Геометричний метод знаходження ймовірності
- •6. Умовні ймовірності, незалежні події, формула повної ймовірності, формула Байєса
- •Дискретні випадкові величини, математичне сподівання та дисперсія
- •Загальне поняття випадкової величини, функції від випадкових величин
- •Граничні теореми
- •0.74 1.12 3.75 4.33 5.71 6.09 7.89 8.03 9.55 10.22.
- •Список використаної літератури
5. Геометричний метод знаходження ймовірності
Розглядається
експеримент з рівноможливими наслідками,
які можна зобразити точками деякої
області
![]()
![]() -вимірного
простору
-вимірного
простору
![]() ;
;![]() – це простір елементарних подій. Подіями
є всі вимірні підмножини області
– це простір елементарних подій. Подіями
є всі вимірні підмножини області![]() .
“Рівноможливість” наслідків означає,
що ймовірність попадання точки у будь-яку
підмножину
.
“Рівноможливість” наслідків означає,
що ймовірність попадання точки у будь-яку
підмножину![]() пропорційна її мірі (довжині, площі,
об’єму тощо) і не залежить від розташування
та форми
пропорційна її мірі (довжині, площі,
об’єму тощо) і не залежить від розташування
та форми![]() .
У цьому випадку може бути використаний
геометричний метод знаходження
ймовірності, згідно з яким ймовірність
події
.
У цьому випадку може бути використаний
геометричний метод знаходження
ймовірності, згідно з яким ймовірність
події![]() визначається за формулою:
визначається за формулою:
![]() ,
(19)
,
(19)
де
![]() – міра Лебега на
– міра Лебега на![]() .
Розглянемо деякі типові приклади.
.
Розглянемо деякі типові приклади.
Приклад
1 (задача
про зустріч). Два приятелі домовилися
зустрітися протягом певного часу
![]() .
Перший приятель може чекати другого не
більше ніж час
.
Перший приятель може чекати другого не
більше ніж час![]() ,
а другий чекає першого лише час
,
а другий чекає першого лише час![]() .
Чому дорівнює ймовірність зустрічі
приятелів, якщо кожен з них незалежно
від іншого може прийти рівноймовірно
у будь-який момент проміжку часу
.
Чому дорівнює ймовірність зустрічі
приятелів, якщо кожен з них незалежно
від іншого може прийти рівноймовірно
у будь-який момент проміжку часу![]() .
.
Розв’язання.
Позначимо моменти приходу першого та
другого приятелів через
![]() та
та![]() відповідно. Тоді простір елементарних
подій
відповідно. Тоді простір елементарних
подій![]() має вигляд (рис. 2):
має вигляд (рис. 2):
![]()

Рис. 2.
Множина
![]() точок, що сприяють зустрічі, визначається
нерівностями
точок, що сприяють зустрічі, визначається
нерівностями
![]()
Очевидно, що
![]() ,
,
![]()
Тому згідно з (19) маємо
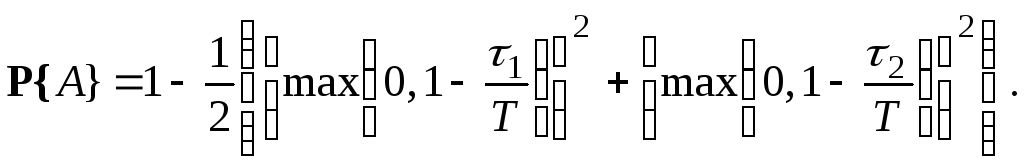
Приклад
2 (голка
Бюффона).
Розглянемо
площину, що розділена паралельними
прямими, які знаходяться на відстані
![]() одна від одної (рис. 3). На площину навмання
кидається голка, що має довжину
одна від одної (рис. 3). На площину навмання
кидається голка, що має довжину![]() .
Треба знайти ймовірність того, що голка
перетне хоча б одну з прямих (у випадку
.
Треба знайти ймовірність того, що голка
перетне хоча б одну з прямих (у випадку![]() голка може перетнути декілька прямих).
голка може перетнути декілька прямих).
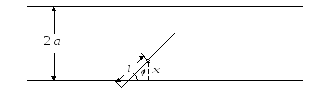
Рис. 3.
Розв’язання.
Положення голки однозначно визначається
відстанню
![]() від центра голки до найближчої прямої
та кутом
від центра голки до найближчої прямої
та кутом![]() ,
що утворює голка з цією прямою. Очевидно,
що
,
що утворює голка з цією прямою. Очевидно,
що![]() і
і![]() ,
тобто простір елементарних подій
,
тобто простір елементарних подій![]() є прямокутником (рис. 4 та 5):
є прямокутником (рис. 4 та 5):
![]()
Для
того, щоб голка перетнула одну з прямих
необхідно і достатньо виконання умови
![]() ,
тобто
,
тобто
![]()
Розглянемо два випадки.
А.
![]() (рис. 4). Очевидно, що
(рис. 4). Очевидно, що
![]() ,
,
![]()
![]()
В.
![]() (рис. 5). У цьому випадку маємо
(рис. 5). У цьому випадку маємо
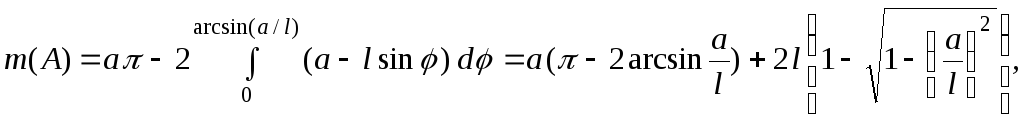
![]()

У
випадку
![]() за допомогою голки Бюффона можна
наближено обчислити число
за допомогою голки Бюффона можна
наближено обчислити число![]() .
Дійсно, нехай було проведено
.
Дійсно, нехай було проведено![]() експериментів, в кожному з яких
досліджувалось чи перетнула голка
пряму, чи ні. Позначимо через
експериментів, в кожному з яких
досліджувалось чи перетнула голка
пряму, чи ні. Позначимо через![]() кількість експериментів, у яких відбувся
перетин. Згідно з посиленим законом
великих чисел
кількість експериментів, у яких відбувся
перетин. Згідно з посиленим законом
великих чисел
![]() з
ймовірністю 1.
з
ймовірністю 1.
Звідси випливає, що
![]() з
ймовірністю 1,
з
ймовірністю 1,
тобто
за допомогою достатньої кількості
експериментів можна обчислити число
![]() з будь-якою точністю.
з будь-якою точністю.
Приклад 3 (парадокс Бертрана). У колі навмання будується хорда. Чому дорівнює ймовірність того, що її довжина перевищує довжину сторони рівностороннього трикутника, вписаного в це коло?
Розв’язання
1.
Розглянемо коло з довільним діаметром
![]() .
З міркувань симетрії можна наперед
визначити напрямок хорди
.
З міркувань симетрії можна наперед
визначити напрямок хорди![]() (рис. 6). Проведемо діаметр
(рис. 6). Проведемо діаметр![]() ,
що перпендикулярний цьому напрямку.
Хорда
,
що перпендикулярний цьому напрямку.
Хорда![]() може перетнути діаметр
може перетнути діаметр![]() у будь-якій його точці (міра цих точок
дорівнює
у будь-якій його точці (міра цих точок
дорівнює![]() ).
В той же час лише точки, що лежать у
проміжку від
).
В той же час лише точки, що лежать у
проміжку від![]() до
до![]() задовольняють умові задачі. Тобто шукана
ймовірність дорівнює
задовольняють умові задачі. Тобто шукана
ймовірність дорівнює![]() .
.
Рис. 7.
Розв’язання
2.
З міркувань симетрії можна наперед
зафіксувати один з кінців хорди на колі
у деякій довільній точці
![]() (рис. 7). Побудуєморівносторонній
трикутник
(рис. 7). Побудуєморівносторонній
трикутник
![]() ,
вписаний у коло. Легко бачити, що дотична
,
вписаний у коло. Легко бачити, що дотична![]() до кола у точці
до кола у точці![]() та дві сторони трикутника
та дві сторони трикутника![]() і
і![]() розбивають кут у
розбивають кут у![]() на три рівні частини. Довжина хорди
на три рівні частини. Довжина хорди![]() перевищує довжину сторони рівностороннього
трикутника тоді і тільки тоді, коли ця
хорда проходить всередині кута
перевищує довжину сторони рівностороннього
трикутника тоді і тільки тоді, коли ця
хорда проходить всередині кута![]() .
Тому ймовірність бажаної події дорівнює
.
Тому ймовірність бажаної події дорівнює![]() .
.
Розв’язання
3.
Для того, щоб визначити положення хорди,
достатньо задати місцезнаходження її
середини (рис. 8). Хорда задовольняє умову
задачі, якщо її центр попадає в середину
кола, вписаного у правильний трикутник
![]() .
Радіус цього кола удвічі менший за
радіус описаного кола.Оскільки
площа круга пропорційна квадрату його
радіуса, то ймовірність
бажаної події дорівнює
.
Радіус цього кола удвічі менший за
радіус описаного кола.Оскільки
площа круга пропорційна квадрату його
радіуса, то ймовірність
бажаної події дорівнює
![]() .
.

З’ясуємо, чому були отримані три різні відповіді, на перший погляд, однієї й тієї ж задачі. Відповідь криється у першій же фразі у постановці задачі: “У колі навмання будується хорда”. Термін “навмання” допускає неоднозначність інтерпретації. В залежності від інтерпретації розв’язуються фактично три різні задачі.
У
першому випадку центр хорди рухається
уздовж фіксованого діаметру кола
(одновимірна задача), у той час як у
третьому випадку центр хорди може
попасти у будь-яку точку круга (двовимірна
задача). У другому ж випадку хорда
закріплюється на шарнірі у точці
![]() кола і її положення визначається кутом
із дотичною до кола у точці
кола і її положення визначається кутом
із дотичною до кола у точці![]() ,
який може приймати значення від
,
який може приймати значення від![]() до
до![]() (також одновимірна задача).
(також одновимірна задача).
