4. Класичне означення ймовірності

Експеримент називають стохастичним (імовірнісним, випадковим), якщо його результат не можна напевне передбачити. З кожним стохастичним експериментом пов’язують простір елементарних подій – сукупність можливих наслідків експерименту.Випадкові події – це підмножини у просторі елементарних подій . Якщо розглядається стохастичний експеримент, який маєоднаково можливих наслідків, а подіїсприяєз них, то ймовірність цієї події дорівнюєФормула включень та виключень: якщо – деякі події, то має місце рівність

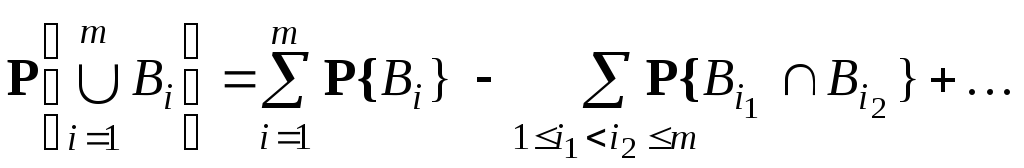(16)

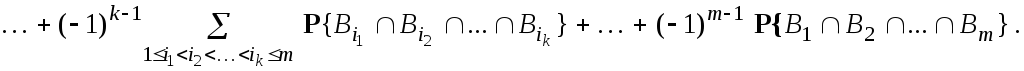
Приклад 1. У наявності є п’ять відрізків, довжини яких дорівнюють відповідно 1, 3, 5, 7 та 9 см. Знайти ймовірність того, що з трьох навмання взятих відрізків можна побудувати трикутник.

Розв’язання. Існує варіантів, якими можна вибрати три відрізка з п’яти.Трикутник може бути побудовано лише тоді, коли виконані умови:

(17)

де – довжини сторін трикутника. З наведених в умові задачі довжин лише три комбінаціїізадовольняють умову (17), тобто . Звідси випливає, що

Приклад 2. У групі є студентів. Яка ймовірність того, що принаймні у двох з них збігаються дні народження?

Розв’язання. Рік має 365 днів. День народження кожного з студентів може припадати на будь-який день року (365 варіантів). Тому за правилом множення існує всього варіантів розміщення днів народження студентів. Знайдемо кількість варіантів, коли жодні два студенти не мають деньнародження у той самий день. Для цього треба обчислити кількість способів, якими з 365 днів можна вибрати впорядковану множину з днів. Використовуючи формулу для розміщення з 365 елементів по , маємо . Тому

Приклад 3. У чемпіонаті грає команд. З метою зменшення загальної кількості ігор за жеребом проводиться розбиття команд на дві підгрупи по команд у кожній. Знайти ймовірність того, що дві найсильніші команди попадуть: а) в одну підгрупу; в) у дві різні підгрупи.

Розв’язання. Знайдемо спочатку кількість варіантів, якими команд можна вибрати у першу підгрупу. Для цього достатньо з команд вибрати , тобто Розглянемо випадок, коли дві найсильніші команди попадають в одну підгрупу. Вони можуть попасти або в першу, або у другу підгрупу (2 варіанти). Крім того, до них ще треба додатково з команд вибрати команд (це можна зробити способами). Тому дві найсильніші команди попадуть в одну підгрупу з ймовірністю 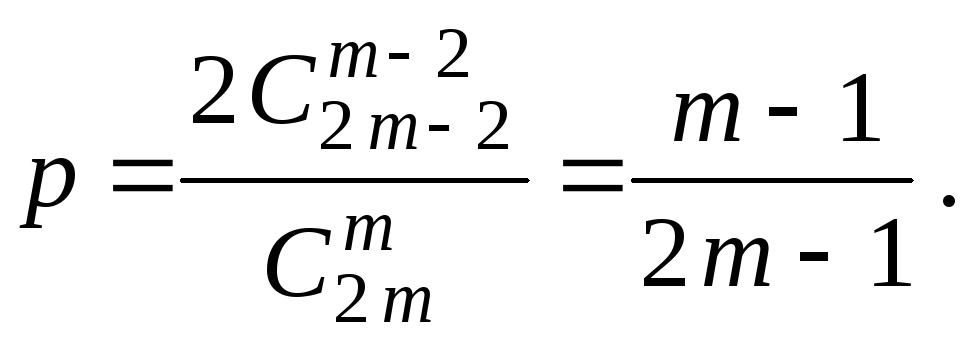Розглянемо подію, що відповідає випадку в). Виберемо ту найсильнішу команду, яка попаде у першу підгрупу (це можна зробити двома способами). У цю ж підгрупу треба ще додатково вибрати команд з команд, що залишилися (способів). Звідси випливає, що дві найсильніші команди попадуть у різні підгрупи з ймовірністю

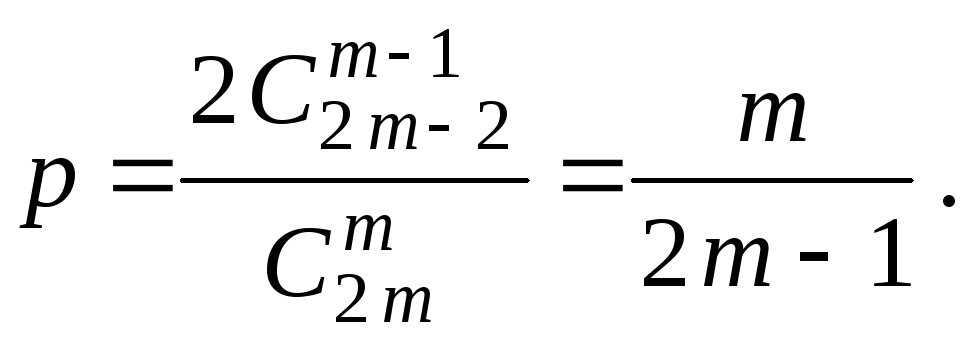
Приклад 4. Знайти ймовірність того, що останні дві цифри у куба навмання взятого невід’ємного цілого числа дорівнюють одиниці.

Розв’язання. Довільне невід’ємне ціле число може бути подане у вигляді, де– деякі цілі числа, що можуть приймати будь-які значення від 0 до 9 включно. Тоді

, (18)

де – деяке ціле число. Звідси випливає, що лишетавпливають на значення двох останніх цифр числа . Тому загальна кількість наслідків експерименту дорівнюєОскільки остання цифра числадорівнює одиниці, то лишезадовольняє цю умову. Крім того, остання цифра числатакож повинна дорівнювати одиниці, тобто згідно з (18) останньою цифрою числамає бути одиниця. Єдиним варіантом є. Звідси випливає, що із 100 варіантів лише один задовольняє умову задачі, тобто

Приклад 5. Кожна з різних частинок попадає в одну з комірок. Яка ймовірність того, що:a) у першу, другу, ..., -ту комірку попадуть відповідно частинок ; b) дана комірка містить частинок;c) в кожній комірці буде принаймні одна частинка ();d) зайнято рівно комірок?

Розв’язання. У випадках a), b) і d) ймовірність бажаної події оцінюється за формулою Для кожної з різних частинок є варіантів попасти в одну з комірок. Тому за правилом множення маємо загальну кількість варіантів . Обчислимо кількістьваріантів, що відповідають кожній з подій, вказаних в умові задачі.

А. Існує способів, якими можна відібрати частинок у першу комірку. Аналогічно, кількість способів відібрати частинок у другу комірку серед частинок, що залишились, дорівнює . Подібним же чином відбираються частинки і для інших комірок. Тому події a) сприяють способів.

В. Спочатку треба відібрати частинок у фіксовану комірку (це можна зробити способами), а потім частинок розподілити серед комірок ( способів). За правилом множення маємо способів.

С. Ймовірність відповідної події обчислюється за допомогою формули включень та виключень (16). Позначимо через подію “коміркане містить частинок”. Тоді Легко бачити, що для будь-яких

(комірок є пустими;різних частинок можна розмістити укоміркахспособами). Кількість доданків у відповідній сумі дорівнює. Згідно з (16) маємо остаточну відповідь

D. Розв’язання задачі розбиваємо на два кроки: спочатку вибираємо комірок з, які будуть зайнятими (це можна зробити способами), а потім розміщуємо різних частинок у комірок таким чином, щоб жодна з них не була пустою (подібна задача розв’язана у пунктіc) за формулою включень та виключень). Тому остаточно маємо