
- •Т е о р і я й м о в і р н о с т е й т а
- •03056, Київ-56, просп. Перемоги, 37 Зміст
- •1. Елементи комбінаторики
- •2. Біноміальні тотожності
- •3. Формула включень та виключень
- •4. Класичне означення ймовірності
- •5. Геометричний метод знаходження ймовірності
- •6. Умовні ймовірності, незалежні події, формула повної ймовірності, формула Байєса
- •Дискретні випадкові величини, математичне сподівання та дисперсія
- •Загальне поняття випадкової величини, функції від випадкових величин
- •Граничні теореми
- •0.74 1.12 3.75 4.33 5.71 6.09 7.89 8.03 9.55 10.22.
- •Список використаної літератури
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ
“КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”
ФІЗИКО-ТЕХНІЧНИЙ ІНСТИТУТ
Т е о р і я й м о в і р н о с т е й т а
М А Т Е М А Т И Ч Н А С Т А Т И С Т И К А
МЕТОДИЧНІ ВКАЗІВКИ ДО РОЗВ’ЯЗАННЯ ЗАДАЧ
ДЛЯ СТУДЕНТІВ СПЕЦІАЛЬНОСТЕЙ
“ПРИКЛАДНА ФІЗИКА”, “ЗАХИСТ ІНФОРМАЦІЇ В КОМП’ЮТЕРНИХ СИСТЕМАХ ТА МЕРЕЖАХ”,
“ЗАХИСТ ІНФОРМАЦІЇ З ОБМЕЖЕНИМ
ДОСТУПОМ ТА АВТОМАТИЗАЦІЯ ЇЇ ОБРОБКИ”
Затверджено Методичною радою НТУУ “КПІ”
Київ
“ПОЛІТЕХНІКА”
2006
Теорія ймовірностей та математична статистика. Методичні вказівки до розв’язання задач для студентів спеціальностей фізико-технічного напряму / Уклад.: М.Ю. Кузнєцов, А.А. Шумська. – К.: ІВЦ «Політехніка», 2006. – хх с.
Гриф надано Методичною радою НТУУ «КПІ»
(Протокол № ____ від _________ 2006 р.)
Н а в ч а л ь н е в и д а н н я
Т Е О Р І Я Й М О В І Р Н О С Т Е Й
Т А М А Т Е М А Т И Ч Н А С Т А Т И С Т И К А
МЕТОДИЧНІ ВКАЗІВКИ ДО РОЗВ’ЯЗАННЯ ЗАДАЧ
для студентів спеціальностей фізико-технічного напрямку
Укладачі: Микола Юрійович Кузнєцов, д. техн. наук, проф.
Алла Антонівна Шумська, к.ф.-м. наук, доц.
Відповідальний редактор
М.М.Савчук, д.ф.-м.н., проф.
Рецензент О.Є.Архипов, д. техн. наук, проф.
Редактор хххххххххххххххххх
Темплан 2007 р., поз. ххх
Підп.
до друку хх.хх.2007. Формат 60×84
![]() .
Папір друк. № 3. Друк офс.
.
Папір друк. № 3. Друк офс.
Ум. друк. арк. 2,15. Обл.-вид. арк. 2,25. Зам. № ххх. Наклад 200 пр.
___________________________________________________________
Інформаційно-видавничий центр “Політехніка”
Друкарня НТУУ “КПІ”
03056, Київ-56, просп. Перемоги, 37 Зміст
Елементи комбінаторики . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Біноміальні тотожності . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Формула включень та виключень . . . . . . . . . . . . . . . . . . . . . . . . . . 12
Класичне означення ймовірності . . . . . . . . . . . . . . . . . . . . . . . . . . 15
Геометричний метод знаходження ймовірності . . . . . . . . . . . . . . . 18
Умовні ймовірності, незалежні події, формула повної ймовір-
ності, формула Байєса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
Дискретні випадкові величини, математичне сподівання та
дисперсія . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
Загальне поняття випадкової величини, функції від випадкових
величин . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
Граничні теореми . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
Елементи математичної статистики . . . . . . . . . . . . . . . . . . . . . . . . . 55
Список використаної літератури . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
1. Елементи комбінаторики
Комбінаторика – це галузь математики, яка досліджує кількість різних комбінацій, які можна отримати із заданого набору об’єктів при виконанні певних умов.
Комбінаторне правило додавання. Нехай
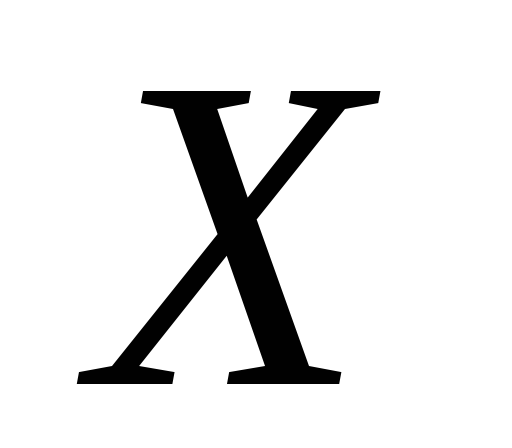 – це деяка множина, яка містить скінчену
кількість елементів,
– це деяка множина, яка містить скінчену
кількість елементів,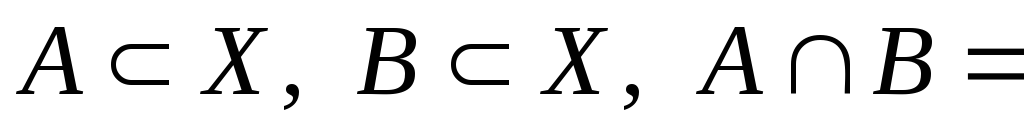 Ø.
Тоді
Ø.
Тоді
![]() (1)
(1)
де
![]() позначає кількість елементів у відповідній
множині. Дане правило узагальнюється
для будь-якої скінченої кількості множин
позначає кількість елементів у відповідній
множині. Дане правило узагальнюється
для будь-якої скінченої кількості множин![]() ,
що попарно не перетинаються:
,
що попарно не перетинаються:
![]()
Приклад 1. У бібліотеці є 5 томів творів Р.Л. Стівенсона та 14 томів творів А. Конан Дойла. Скількома способами можна вибрати для читання один з томів указаних авторів?
Розв’язання.
Нехай
![]() і
і![]() відповідно зібрання творівР.Л.
Стівенсона та А. Конан Дойла. Згідно
з умовою задачі
відповідно зібрання творівР.Л.
Стівенсона та А. Конан Дойла. Згідно
з умовою задачі
![]() Оскільки
Р.Л. Стівенсон та А. Конан Дойл не мають
спільних творів, то згідно з (1) маємо
Оскільки
Р.Л. Стівенсон та А. Конан Дойл не мають
спільних творів, то згідно з (1) маємо
![]()
Комбінаторне правило множення. Якщо множини
 містять відповідно
містять відповідно елементів, то кількість
елементів, то кількість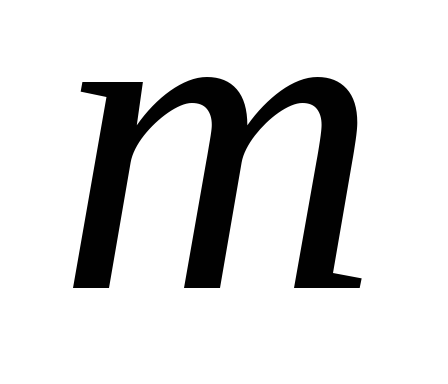 -вимірних
векторів, які отримують вибором по
одному елементу з кожної множини,
дорівнює
-вимірних
векторів, які отримують вибором по
одному елементу з кожної множини,
дорівнює
Приклад 2. Скільки чотирицифрових чисел можна скласти, використовуючи цифри 0, 1, 2, 3, 4, 5?
Розв’язання.
Чотирицифрове число можна розглядати
як чотиривимірний вектор, тому
![]() .
Першою компонентою цього вектора може
бути будь-яка цифра з множини
.
Першою компонентою цього вектора може
бути будь-яка цифра з множини![]() (запис числа не може починатися з 0), а
на інших позиціях може стояти будь-яка
цифра, тобто
(запис числа не може починатися з 0), а
на інших позиціях може стояти будь-яка
цифра, тобто![]() Звідси маємо, що з указаних цифр можна
скласти
Звідси маємо, що з указаних цифр можна
скласти![]() чотирицифрових чисел.
чотирицифрових чисел.
Комбінації з
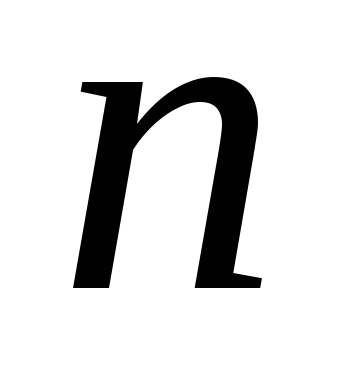 елементів по
елементів по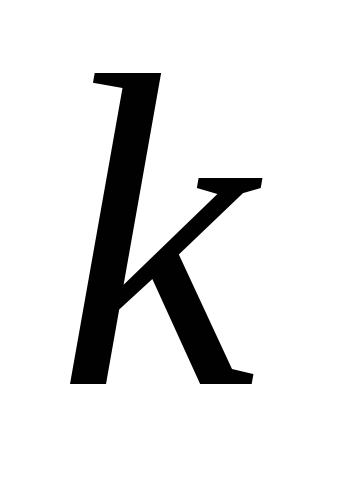 .Якщо
деяка множина містить
.Якщо
деяка множина містить
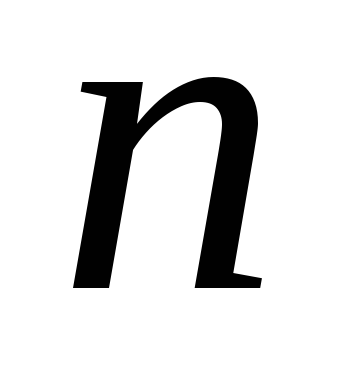 елементів,
то кількість її
елементів,
то кількість її
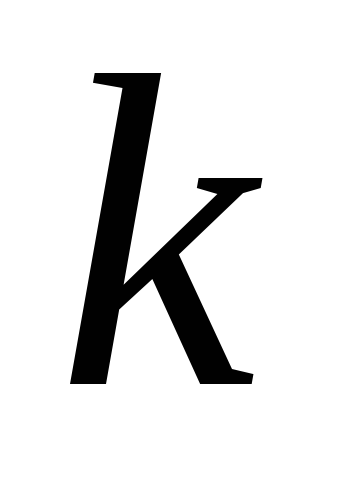 -елементних
підмножин дорівнює
-елементних
підмножин дорівнює
![]() (2)
(2)
де
![]() Вважається, що
Вважається, що![]()
Приклад
3.
У шаховому турнірі приймали участь
![]() шахістів, причому кожні 2 шахісти
зустрілися по одному разу. Скільки
усього партій зіграли учасники турніру?
шахістів, причому кожні 2 шахісти
зустрілися по одному разу. Скільки
усього партій зіграли учасники турніру?
Розв’язання.
Кількість зіграних партій дорівнює
кількості двоелементних підмножин у
множині з
![]() елементів, тобто
елементів, тобто![]()
Приклад
4.
У скількох точках перетинаються діагоналі
опуклого
![]() -кутника,
якщо жодні три з них не перетинаються
в одній точці?
-кутника,
якщо жодні три з них не перетинаються
в одній точці?
Розв’язання.
Кожним чотирьом вершинам
![]() -кутника
можна поставити у відповідність лише
одну точку перетину діагоналей, і
навпаки, кожній
точці перетину двох діагоналей
відповідають чотири вершини
-кутника
можна поставити у відповідність лише
одну точку перетину діагоналей, і
навпаки, кожній
точці перетину двох діагоналей
відповідають чотири вершини
![]() -кутника.
Тому кількість точок перетину діагоналей
співпадає з кількістю способів, якими
можна вибрати 4 вершини з
-кутника.
Тому кількість точок перетину діагоналей
співпадає з кількістю способів, якими
можна вибрати 4 вершини з![]() можливих, тобто
можливих, тобто![]()
Приклад
5.
Скількома способами можна розташувати
![]() нулів та
нулів та![]() одиниць (
одиниць (![]() )
таким чином, щоб жодні дві одиниці не
стояли поруч?
)
таким чином, щоб жодні дві одиниці не
стояли поруч?
Розв’язання.
Ця задача належить до так званих
комбінаторних задач з обмеженнями.
Розташуємо
![]() нулів. Очевидно, що кожна одиниця має
можливість займати позицію лише між
нулями, причому між сусідніми нулями
може стояти не більше однієї одиниці.
Таким чином, існує
нулів. Очевидно, що кожна одиниця має
можливість займати позицію лише між
нулями, причому між сусідніми нулями
може стояти не більше однієї одиниці.
Таким чином, існує![]() позиція, куди можна поставити одиниці
(враховуються позиції перед першим
нулем та за останнім нулем). Серед цих
позиція, куди можна поставити одиниці
(враховуються позиції перед першим
нулем та за останнім нулем). Серед цих![]() позицій треба обрати
позицій треба обрати![]() позицій, де будуть розташовані одиниці.
Це можна зробити
позицій, де будуть розташовані одиниці.
Це можна зробити![]() способами.
способами.
Біном Ньютона:
![]() (3)
(3)
Приклад
6.
Скільки раціональних членів містить
розклад
![]() ?
?
Розв’язання. Використовуючи формулу (3), маємо
![]() (4)
(4)
Члени
розкладу (4) будуть раціональними лише
у тому випадку, коли
![]() та
та![]() будуть цілими числами, тобто
будуть цілими числами, тобто![]() повинно одночасно ділитися на 2 і на 3.
Усього таких чисел буде 16.
повинно одночасно ділитися на 2 і на 3.
Усього таких чисел буде 16.
Множина з
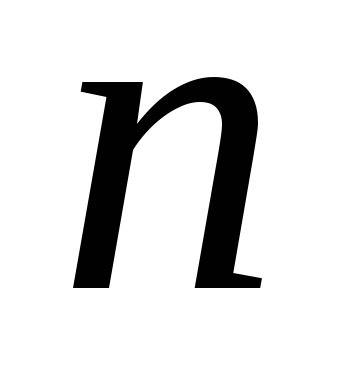 елементів називаєтьсявпорядкованою,
якщо кожному її елементу поставлено у
відповідність певне число від 1 до
елементів називаєтьсявпорядкованою,
якщо кожному її елементу поставлено у
відповідність певне число від 1 до
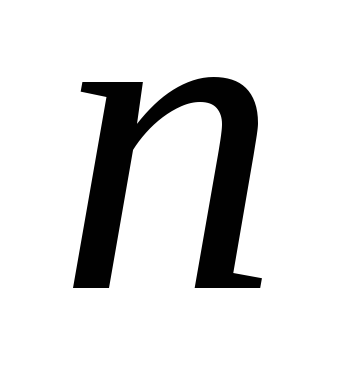 ,
причому різним елементам відповідають
різні числа. Впорядковані множини, які
можна одержати з даної множини, називаютьперестановками
цієї множини. Кількість перестановок
дорівнює
,
причому різним елементам відповідають
різні числа. Впорядковані множини, які
можна одержати з даної множини, називаютьперестановками
цієї множини. Кількість перестановок
дорівнює
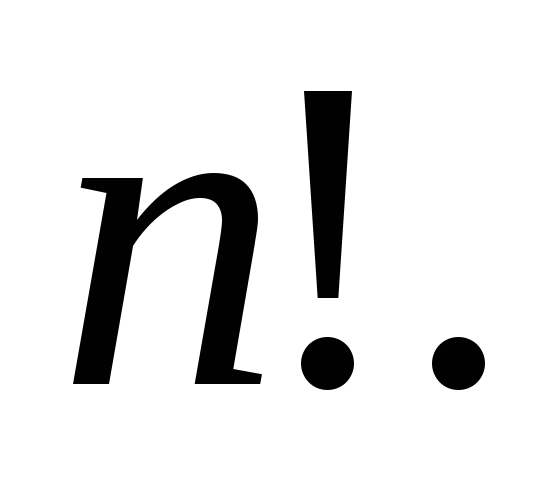
Приклад
7. Скількома
способами можна впорядкувати множину
![]() таким чином, щоб числа 1, 2, 3 завжди стояли
поруч?
таким чином, щоб числа 1, 2, 3 завжди стояли
поруч?
Розв’язання.
Оскільки числа 1, 2 та 3 завжди стоять
поруч, то їх можна розглядати як одне
число (позначимо його
![]() ).
Кількість можливих перестановок чисел
).
Кількість можливих перестановок чисел
![]() дорівнює
дорівнює![]() В той же час потрібно ще врахувати, що
числа 1, 2, 3 можуть стояти у довільному
порядку, тобто кожній перестановці
чисел
В той же час потрібно ще врахувати, що
числа 1, 2, 3 можуть стояти у довільному
порядку, тобто кожній перестановці
чисел![]() відповідає ще
відповідає ще![]() перестановок чисел 1, 2 та 3. Тому загальна
кількість перестановок дорівнює
перестановок чисел 1, 2 та 3. Тому загальна
кількість перестановок дорівнює![]()
Приклад 8. Скількома способами можна розташувати на шаховій дошці 8 тур таким чином, щоб вони не могли бити одна одну?
Розв’язання.
При
вказаному способі розташування тур на
кожній горизонталі та кожній вертикалі
може стояти лише одна тура. Розглянемо
першу вертикаль. Усього існує 8 способів
розташування на ній тури. Якщо перша
тура знайшла своє місце, то для розташування
наступної тури на другій вертикалі
існує лише 7 можливостей (була виключена
горизонталь, на якій розташована перша
тура). Аналогічно, для розташування тури
на третій вертикалі існує всього 6
допустимих позицій. Для останньої
восьмої тури існує лише єдина позиція.
Тому кількість допустимих способів,
якими можуть бути розташованими тури,
дорівнює
![]()
Розміщення з
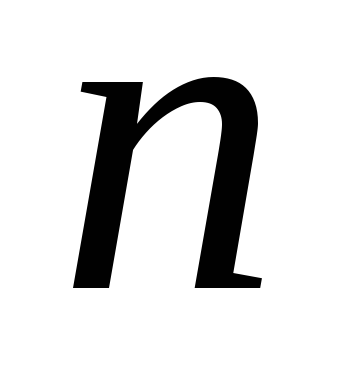 елементів по
елементів по
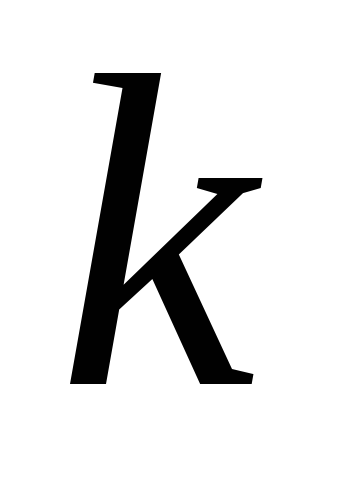 – це впорядковані
– це впорядковані
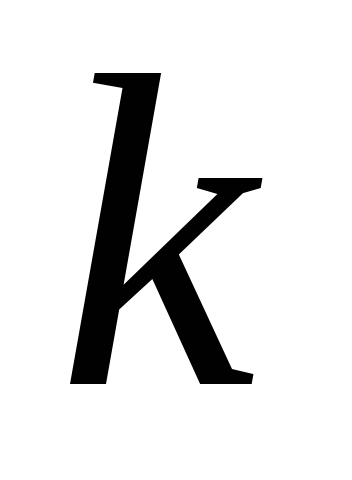 -елементні
підмножини множини, яка складається з
-елементні
підмножини множини, яка складається з
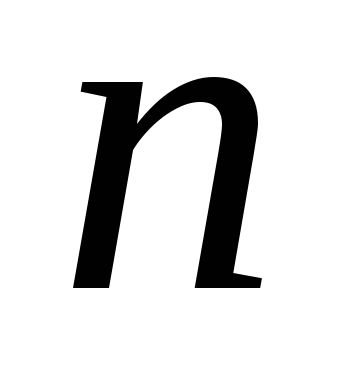 елементів. Кількість розміщень з
елементів. Кількість розміщень з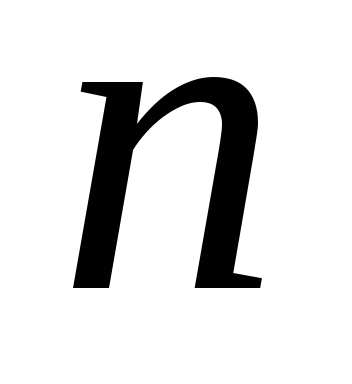 елементів по
елементів по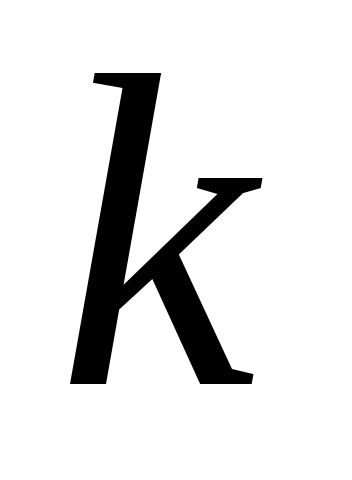 дорівнює
дорівнює
![]()
Приклад 9. Скількома способами можна скласти трьохкольоровий смугастий прапор, якщо у наявності є тканина шести різних кольорів? Якою буде відповідь у випадку, коли одна смуга повинна бути обов’язково червоною?
Розв’язання.
Для
отримання трьох смуг можна використати
6 різних кольорів, тобто з 6 кольорів
треба вибрати впорядковану множину з
трьох кольорів. Кількість таких способів
дорівнює
![]() Якщо ж одна зі смуг має бути червоною,
то її на прапорі можна розташувати
трьома способами. Кожному з цих способів
відповідає
Якщо ж одна зі смуг має бути червоною,
то її на прапорі можна розташувати
трьома способами. Кожному з цих способів
відповідає![]() варіантів, якими можна з п’яти кольорів,
що лишилися, вибрати два. Тому за правилом
множення з червоною смугою можна скласти
варіантів, якими можна з п’яти кольорів,
що лишилися, вибрати два. Тому за правилом
множення з червоною смугою можна скласти![]() прапорів.
прапорів.
Приклад 10. Скільки різних чотирицифрових чисел можна скласти з цифр 0, 1, 2, 3, 4, 5, 6 так, щоб у кожному числі була цифра 1, причому цифри у числі не повинні повторюватись?
Розв’язання.
Розглянемо
два випадки: a)
цифра 1 стоїть на першій позиції у
чотирицифровому числі; b)
цифра 1
займає
будь-яку іншу позицію. У випадку a)
на три позиції, що лишилися, серед 6 цифр
треба вибрати впорядковану підмножину
з 3 цифр. Це можна зробити
![]() способами. У випадкуb)
на
першій позиці може стояти будь-яка
цифра, окрім 0 та 1 (5 варіантів), цифра 1
може стояти на будь-якій з трьох позицій
(3 варіанти), а щоб заповнити 2 позиції,
що лишилися, треба з 5 цифр вибрати
впорядковану множину з двох цифр (
способами. У випадкуb)
на
першій позиці може стояти будь-яка
цифра, окрім 0 та 1 (5 варіантів), цифра 1
може стояти на будь-якій з трьох позицій
(3 варіанти), а щоб заповнити 2 позиції,
що лишилися, треба з 5 цифр вибрати
впорядковану множину з двох цифр (![]() способів). Таким чином випадкуb)
відповідає
способів). Таким чином випадкуb)
відповідає
![]() способів. За правилом додавання маємо
способів. За правилом додавання маємо![]() різних
чотирицифрових чисел, що відповідають
умові задачі.
різних
чотирицифрових чисел, що відповідають
умові задачі.
Комбінації з повтореннями. Припустимо, що кожен з елементів може бути одного з
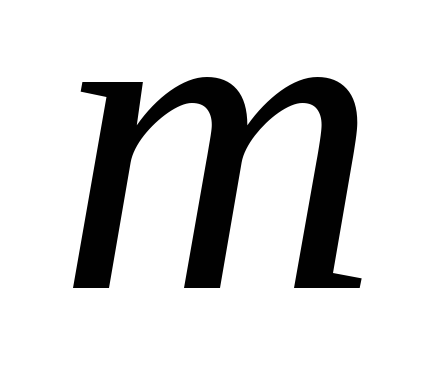 типів. Комбінацією з повтореннями
називається набір з
типів. Комбінацією з повтореннями
називається набір з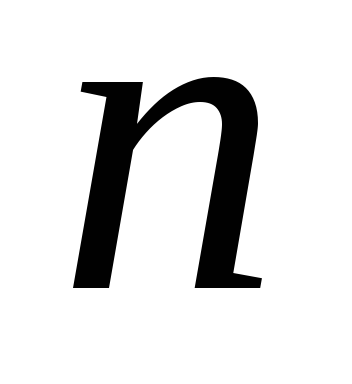 елементів, кожен з яких може бути одного
з
елементів, кожен з яких може бути одного
з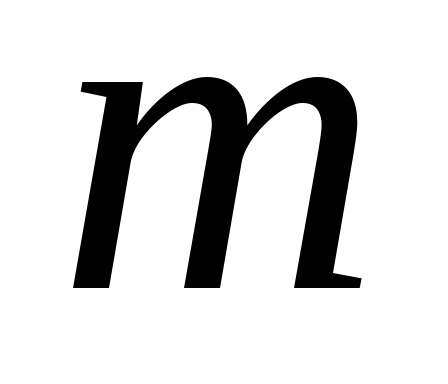 типів. Комбінації відрізняються за
кількістю елементів того чи іншого
типу. Кількість різних комбінацій з
елементів
типів. Комбінації відрізняються за
кількістю елементів того чи іншого
типу. Кількість різних комбінацій з
елементів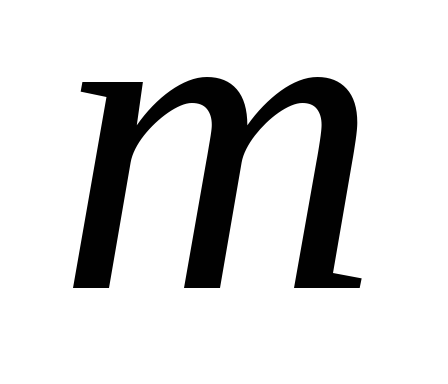 типів по
типів по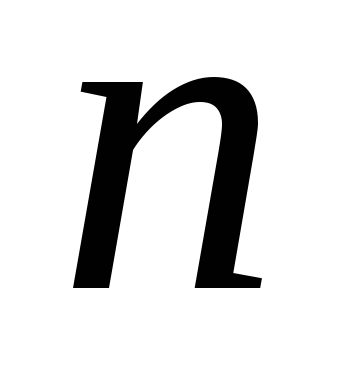 з повтореннями дорівнює
з повтореннями дорівнює
![]() (5)
(5)
Приклад 11. У кондитерському магазині продаються тістечка п’яти видів – наполеони, еклери, пісочні, медовики та заварні. Скількома способами можна купити 8 тістечок?
Розв’язання.
Це
типова задача на комбінації з повтореннями,
коли є
![]() типів елементів і треба вибрати
типів елементів і треба вибрати![]() елементів. Згідно з (5) маємо
елементів. Згідно з (5) маємо![]() комбінацій. Але ця задача належить якраз
до тих задач, коли інтерес викликає не
стільки відповідь, скільки метод
розв’язання задачі, який може бути
застосований у багатьох інших ситуаціях.
Цей метод носить назвуметоду
перегородок.
Розташуємо всі куплені тістечка в такому
порядку: спочатку викладемо наполеони,
далі еклери, потім пісочні, за ними
медовики і нарешті заварні. Щоб відділити
різні типи тістечок, поставимо між ними
4 перегородки. Позначимо тістечко
символом “0”,
а перегородку символом “1”.
Тоді набір куплених тістечок однозначно
характеризується послідовністю з 8
нулів та 4 одиниць. Наприклад, послідовність
100010110000 означає, що було куплено 0
наполеонів, 3 еклери, 1 пісочне, 0 медовиків
та 4 заварних. Очевидно кількість
способів, якими можна купити 8 тістечок,
співпадає з кількістю різних послідовностей
указаного виду. Послідовність визначається
однозначно, якщо вибрати 4 місця з 12, де
будуть розташовані одиниці. Кількість
таких комбінацій дорівнює
комбінацій. Але ця задача належить якраз
до тих задач, коли інтерес викликає не
стільки відповідь, скільки метод
розв’язання задачі, який може бути
застосований у багатьох інших ситуаціях.
Цей метод носить назвуметоду
перегородок.
Розташуємо всі куплені тістечка в такому
порядку: спочатку викладемо наполеони,
далі еклери, потім пісочні, за ними
медовики і нарешті заварні. Щоб відділити
різні типи тістечок, поставимо між ними
4 перегородки. Позначимо тістечко
символом “0”,
а перегородку символом “1”.
Тоді набір куплених тістечок однозначно
характеризується послідовністю з 8
нулів та 4 одиниць. Наприклад, послідовність
100010110000 означає, що було куплено 0
наполеонів, 3 еклери, 1 пісочне, 0 медовиків
та 4 заварних. Очевидно кількість
способів, якими можна купити 8 тістечок,
співпадає з кількістю різних послідовностей
указаного виду. Послідовність визначається
однозначно, якщо вибрати 4 місця з 12, де
будуть розташовані одиниці. Кількість
таких комбінацій дорівнює
![]()
Приклад
12. Скільки
цілих невід’ємних розв’язків має
рівняння
![]() ?
?
Розв’язання.
Сформульована
задача має таку інтерпретацію. Треба
купити
![]() тістечок, яких може бути
тістечок, яких може бути![]() видів,
видів,![]() – кількість куплених тістечок
– кількість куплених тістечок![]() -го
виду. Аналогічно попередньому прикладу,
використовуючи
-го
виду. Аналогічно попередньому прикладу,
використовуючи![]() перегородку, маємо відповідь
перегородку, маємо відповідь![]() .
.
Перестановки з повтореннями. Припустимо, що множина містить
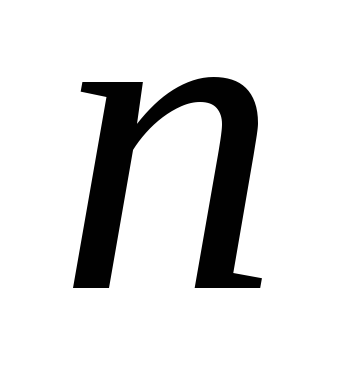 елементів
елементів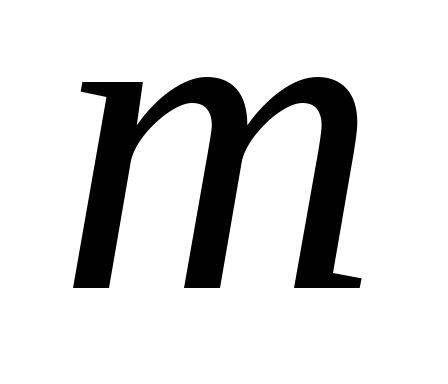 різних типів, а саме, у множину входять
різних типів, а саме, у множину входять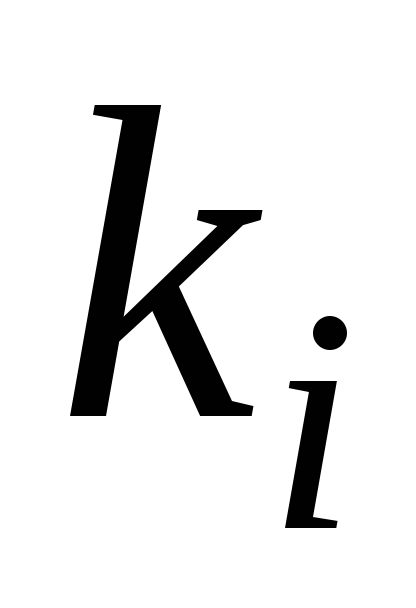 елементів
елементів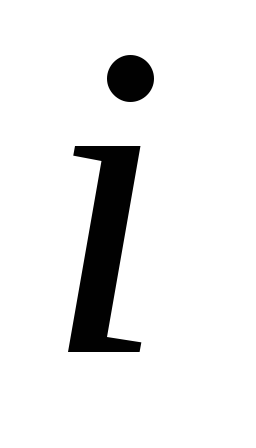 -го
типу (
-го
типу ( ),
причому
),
причому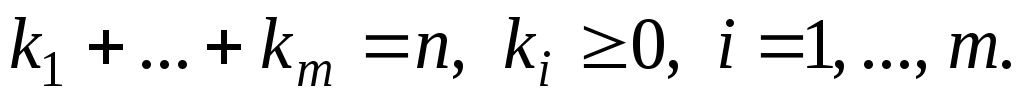 Кількість різних перестановок з
повтореннями дорівнює
Кількість різних перестановок з
повтореннями дорівнює
![]() (6)
(6)
Числа
![]() називаютьсяполіноміальними
коефіцієнтами.
називаютьсяполіноміальними
коефіцієнтами.
Приклад 13. Скільки різних слів можна утворити з букв слова “периметр” (слова не обов’язково мають смисловий зміст)?
Розв’язання.
У
даному випадку маємо множину, що містить
![]() букв
букв![]() типів, причому букви“е”
та “р”
зустрічаються по 2 рази, решта букв –
по одному разу. Тому згідно з (6) кількість
різних перестановок дорівнює
типів, причому букви“е”
та “р”
зустрічаються по 2 рази, решта букв –
по одному разу. Тому згідно з (6) кількість
різних перестановок дорівнює
![]()
Приклад 14. Ліфт із 9 пасажирами зупиняється на п’яти поверхах. Пасажири виходять групами по дві, три та чотири особи. Скількома способами це може відбутися, якщо на кожному поверсі може вийти не більше однієї групи пасажирів?
Розв’язання.
Для визначення загальної кількості
варіантів потрібно зробити три кроки:
1) вибрати три поверхи, на яких виходять
групи пасажирів (очевидно, це можна
зробити
![]() способами); 2) визначити, які саме групи
пасажирів виходять на цих поверхах (
способами); 2) визначити, які саме групи
пасажирів виходять на цих поверхах (![]() способів); 3) з’ясувати, які саме
пасажири входять у ці три групи (це можна
зробити
способів); 3) з’ясувати, які саме
пасажири входять у ці три групи (це можна
зробити![]() способами). За правилом множення загальна
кількість комбінацій дорівнює
способами). За правилом множення загальна
кількість комбінацій дорівнює
![]()
Поліноміальна формула:
![]() (7)
(7)
Приклад 15. Скільки членів містить поліноміальний розклад (7)?
Розв’язання.
Поставлене
питання можна сформулювати таким чином:
скільки цілих невід’ємних розв’язків
має рівняння
![]() ?
Відповідь була наведена у прикладі 12.
Методом перегородок отримуємо
?
Відповідь була наведена у прикладі 12.
Методом перегородок отримуємо
![]() членів у правій частині формули (7).
членів у правій частині формули (7).
Приклад
16. Знайти
коефіцієнти при
![]() та
та![]() у розкладі
у розкладі![]()
Розв’язання. Згідно з формулою (7) маємо
![]()
Існує
лише одне значення
![]() ,
що задовольняє умову
,
що задовольняє умову![]() З рівняння
З рівняння![]() знаходимо, що
знаходимо, що![]() .
Таким чином, коефіцієнт при
.
Таким чином, коефіцієнт при
![]() дорівнює
дорівнює
![]()
![]() В той же час не існує цілих невід’ємних
В той же час не існує цілих невід’ємних![]() таких, що
таких, що![]() Тому відповідний коефіцієнт при
Тому відповідний коефіцієнт при
![]() дорівнює нулю.
дорівнює нулю.
