Конспект лекцій з фізики.

Електрика і магнетизм.

За редакцією Заболотної Т.Г.

Електромагнетизм

Електромагнетизм – розділ фізики, що досліджує властивості електромагнітного поля та взаємодію з цим полем інших видів матерії.

Теорія електромагнітних неквантових явищ називається класичною електродинамікою.

Виділяють чотири типи взаємодій:

1) гравітаційна ( );

2) електромагнітна ();

3) сильна взаємодія – ядерна (, короткодіюча);

4) слабка взаємодія – між вільними елементарними частинками (, короткодіюча).

Структура матерії в ділянці просторових масштабів 10^-4–10^-18зумовлена електромагнітною взаємодією. Для порівняння:. З чотирьох відомих взаємодій лише електромагнітна може бути використана для керування зарядженими частинками. На законах електродинаміки базуються електротехнічні, радіотехнічні та інші прилади.

Електростатика – вчення про властивості та взаємодію електричних зарядів, нерухомих відносно обраної для їх вивчення системи координат.

Розділ 1. Електростатичне поле в вакуумі.

§1 Електричний заряд та його характеристики. Закон збереження електричного заряду.

Електричний заряд – фізична характеристика частинки, яка визначає інтенсивність електромагнітної взаємодії.

[q]=Кл (Кулон)

Властивості:

1) заряд не є знаковизначеною величиною;

2) адитивність;

3) релятивістсько-інваріантний;

4) кратність: Q=±Ne, де e=1,6·10^-19Кл.

5) сталість:

§2 Закон Кулона.

Закон взаємодії електричних зарядів відкритий Шарлем Кулоном в 1785 р. за допомогою крутильних ваг.

Розглянемо два позитивних електричних заряди, відстань між якими задається вектором . Тоді на заряд 1 діє з боку заряду 2 сила:

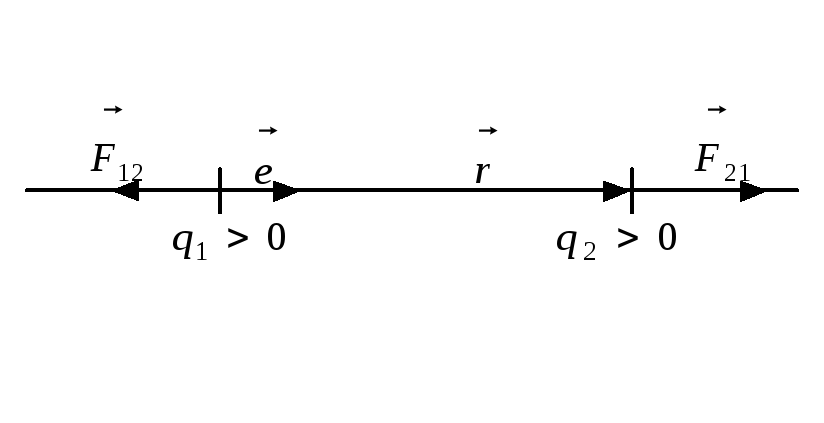
(1.1)

Одночасно на заряд 2 з боку заряду 1 діє сила . В системі СІ значення коефіцієнтаkприймають за, де– електрична стала. Тоді закон Кулона запишеться у вигляді:

(1.2)

В системі з N+1 зарядів на заряд діятиме сила:

§3 Напруженість електричного поля.

Напруженість – фізична величина, яка чисельно дорівнює силі, що діє на одиничний позитивний заряд в даній точці поля.

(1.3)

Розглянемо поле, яке утворює точковий заряд. Сила, що діє на деякий інший заряд, що вміщений в поле досліджуваного дорівнює: , тоді напруженість.

Ч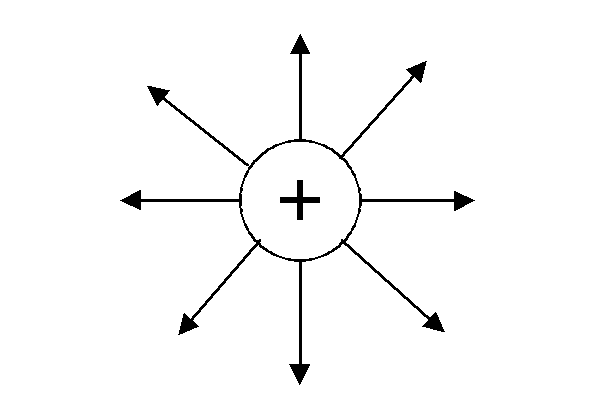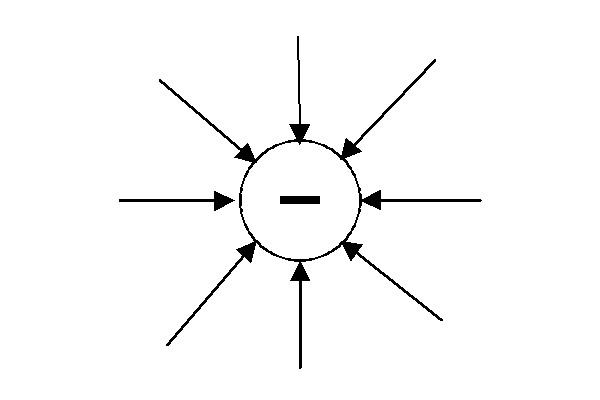асто для опису електричного поля використовують графічне зображення. На них поле зображують кривими, які називають силовими лініями електричного поля. Їх будують так, щоб в кожній точці напрямок дотичної до лінії збігався з напрямком вектора напруженості в цій точці.

Поле сильніше там, де густина ліній більша, тобто

(1.4)

Принцип суперпозиції дозволяє розглядати поля, утворені різними зарядами, незалежно один від одного. При цьому . Цей принцип дозволяє розв’язати основну задачу електростатики: по заданому розподілу зарядів визначити напруженість поля.

Розподіл зарядів:

1) лінійний:;

2) поверхневий: ;

3) об’ємний: .

Алгоритм розв’язання основної задачі електростатики:

1) відповідно до умови поділяють тіло на елементарні частини (dl, dS, dV);

2) обчислюють заряд, локалізований в даному елементі ();

3) обчислюють ;

4) знаходять напруженість інтегруванням за l, S чи V.

Приклад: Обчислити напруженість поля, утвореного нескінченною довгою одноріднозарядженою ниткою з лінійною густиною заряду .

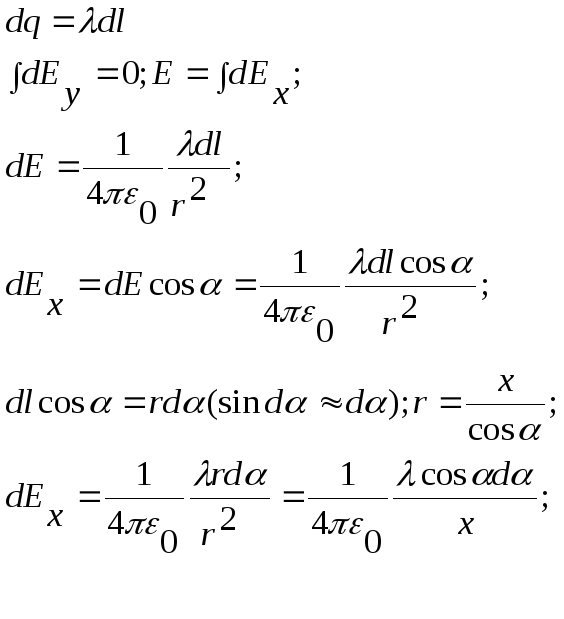
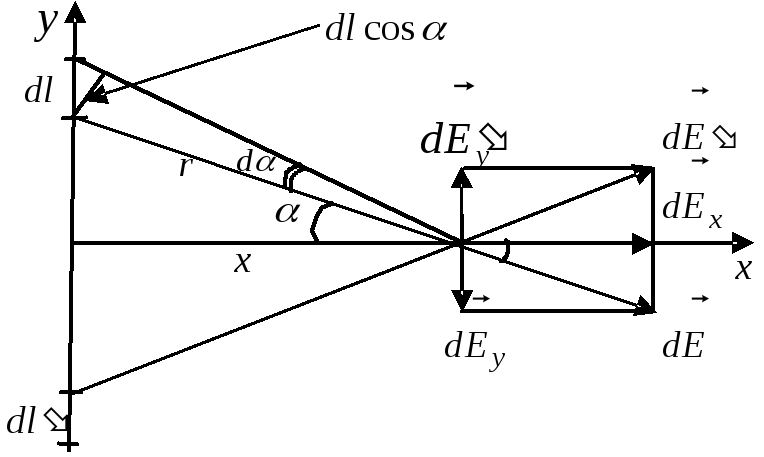
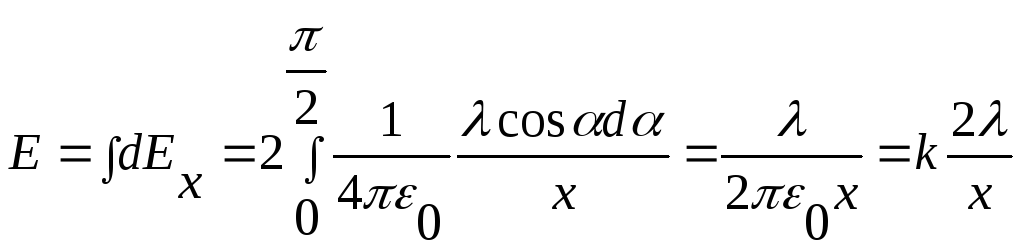
§4 Теорема Гауса.

1. Потік векторного поля.

Розглянемо деяку рідину. Її течію можна характеризувати швидкістю . Об’єм рідини, що проходить в одиницю часу крізь деяку уявну поверхню S, називається потоком рідини крізь цю поверхню.

О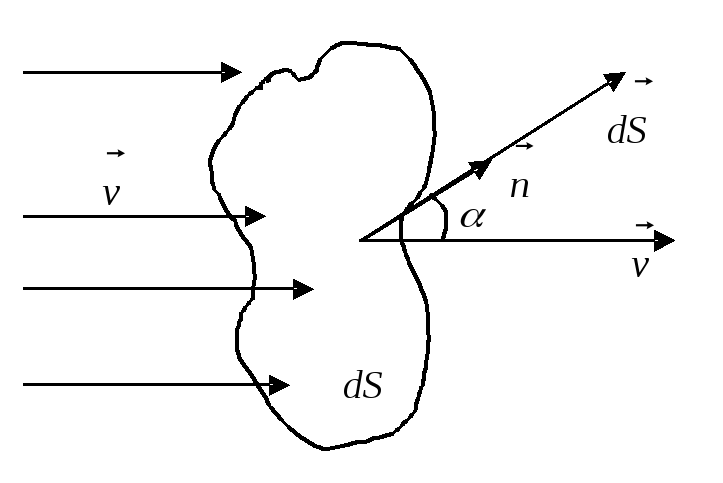бчислимо об’єм рідини, що протікає через поверхню dS за проміжок часу.

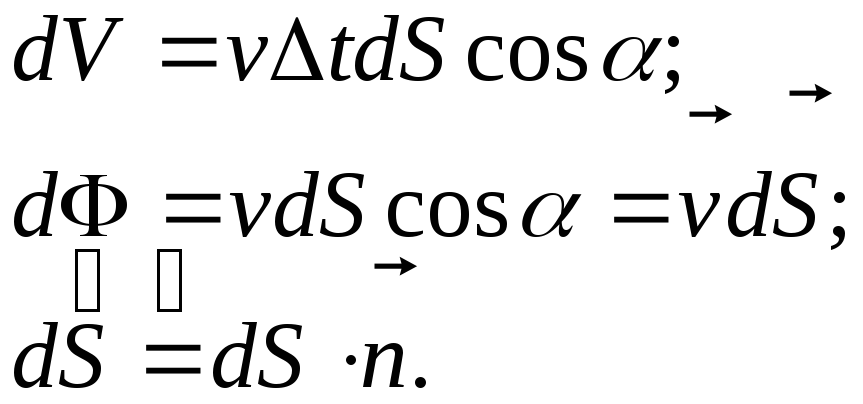
– потік векторного полякрізь площину S. Отже потік– величина скалярна, що залежить від взаємної орієнтаціїі.

Е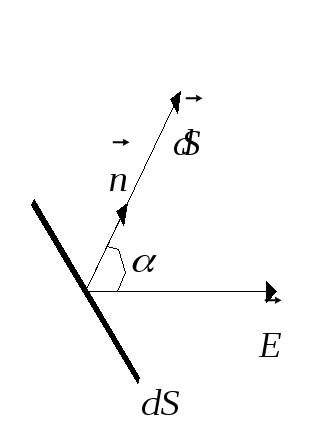лементарний потік:

;

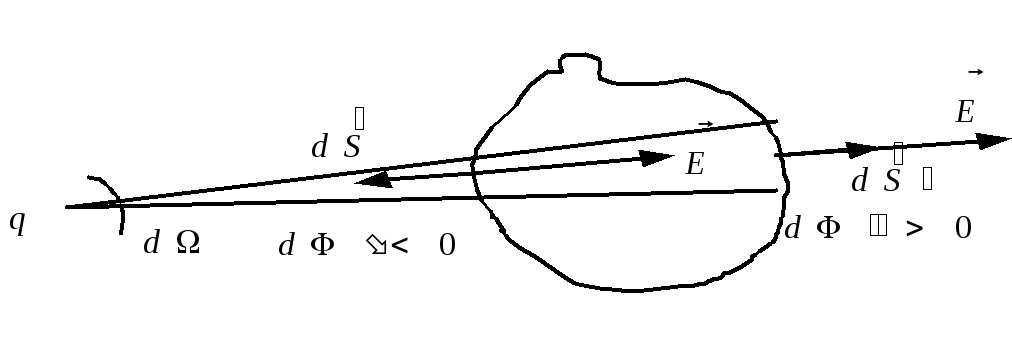
Потік вектора через замкнену поверхню чисельно дорівнює різниці числа ліній, що виходять з неї і що входять.

О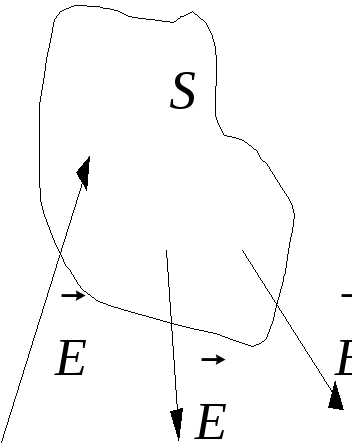кремі випадки:

, лінії йдуть неперервно;

, частина ліній починається в поверхні, існують джерела, +q;

,частина ліній закінчується в поверхні, існують стоки, -q.

Потік – це потужність джерел (стоків) вектора .

2. Теорема Гауса для електричних полів в вакуумі в інтегральній формі.

Розглянемо деяку поверхню S. Обчислимо потік, що протікає через неї.

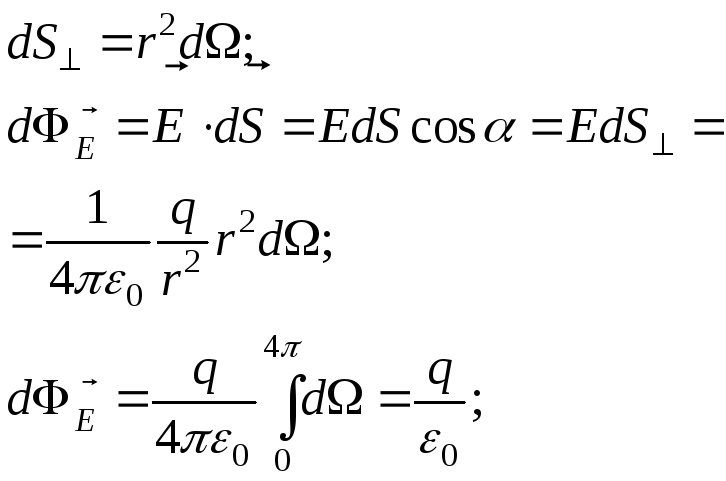
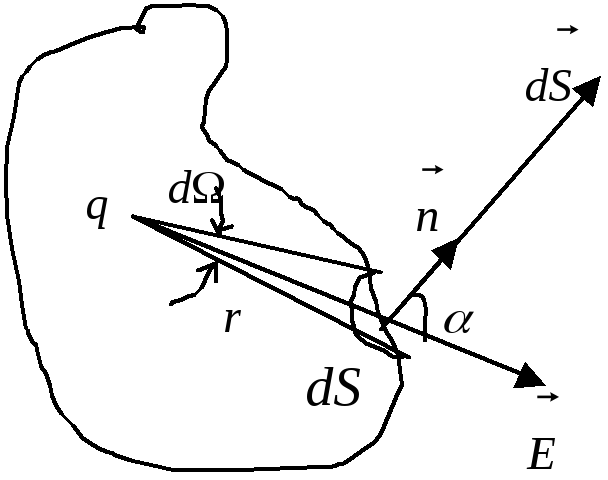
– заряд знаходиться всередині поверхні;

– заряд поза поверхнею.

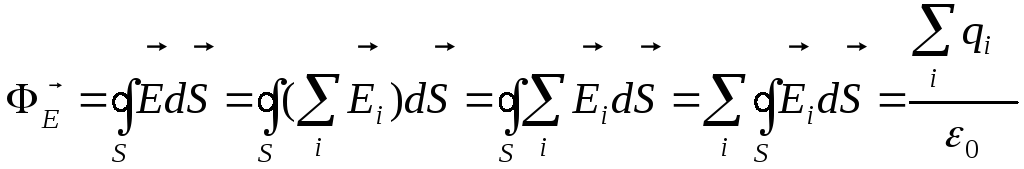
Потік вектора напруженості крізь довільну замкнену поверхню S в вакуумі дорівнює алгебраїчній сумі зарядів, зосереджених в об’ємі, що обмежений цією поверхнею, поділеній на.

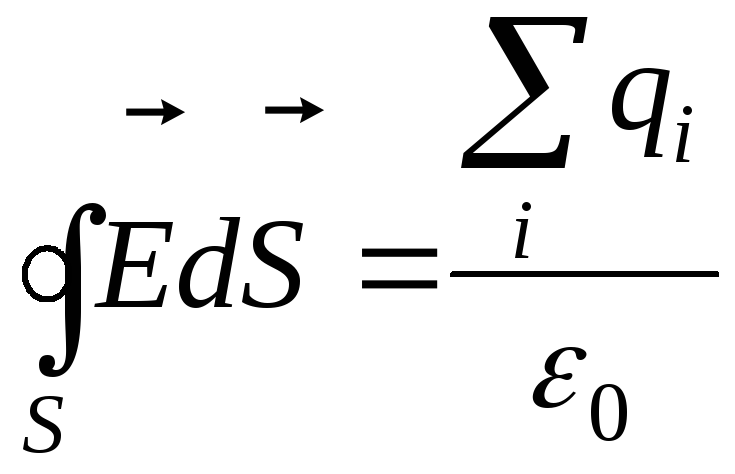
(1.5)

Теорема Гауса і закон Кулона відображають одну і ту саму фундаментальну властивість електростатичного поля: його інтенсивність обернено-пропорційна квадрату відстані від точкового заряду.

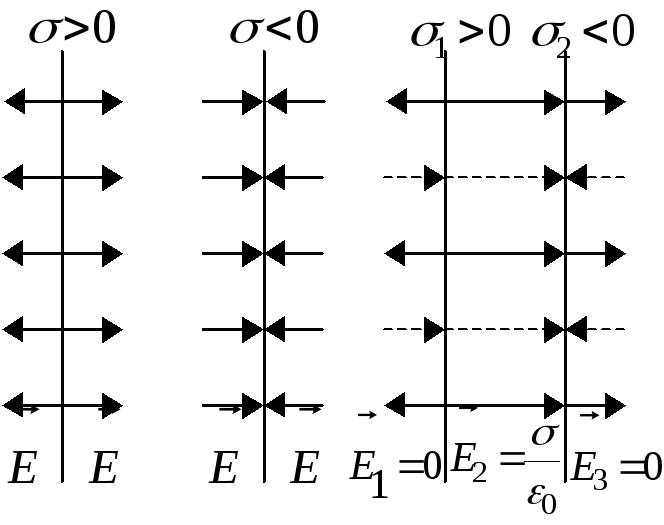
Висновок: оскільки в загальному випадку потік не дорівнює нулю, то лінії електростатичного поля незамкнені. Вони починаються на позитивних зарядах, а закінчуються на негативних.

Доведена теорема в ряді випадків дозволяє розв’язати основну задачу електростатики. Для цього необхідна наявність певної симетрії в розподілі зарядів.

3. Застосування теореми Гауса для розрахунків електричних полів.

А) Поле нескінченої одноріднозарядженої площини.

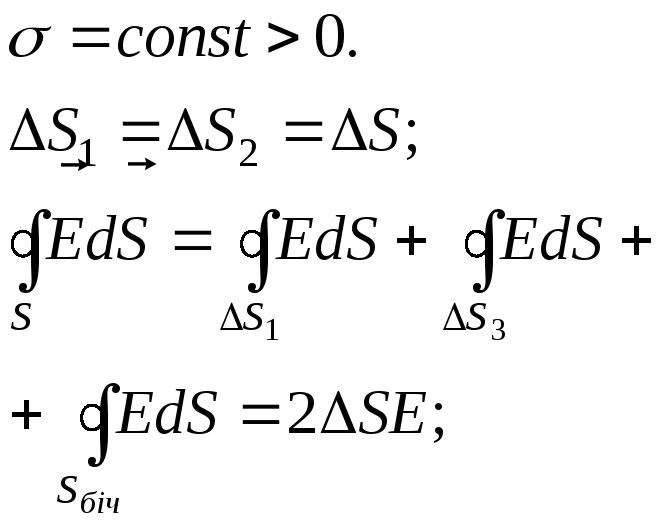
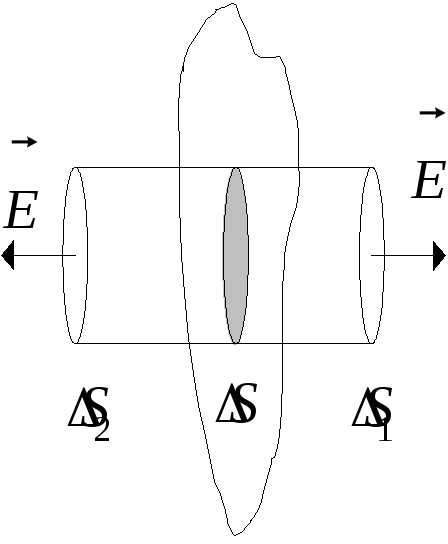
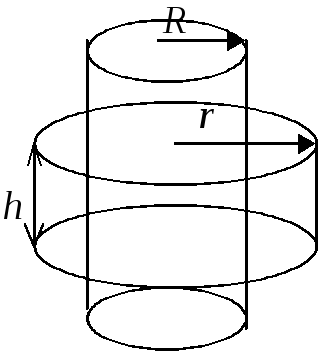
Б) Поле нескінченого одноріднозарядженого круглого циліндру радіуса R.

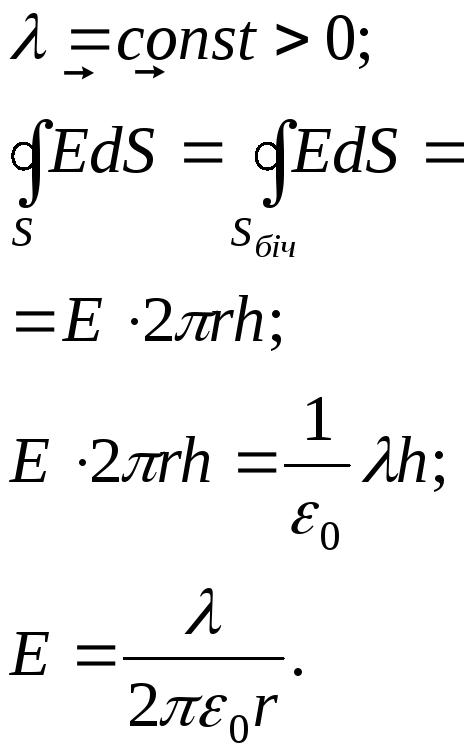
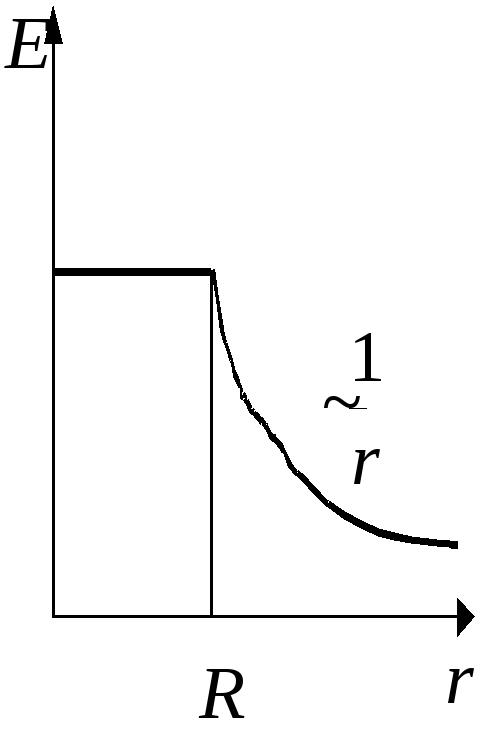
В) Поле одноріднозарядженої кулі радіуса R.

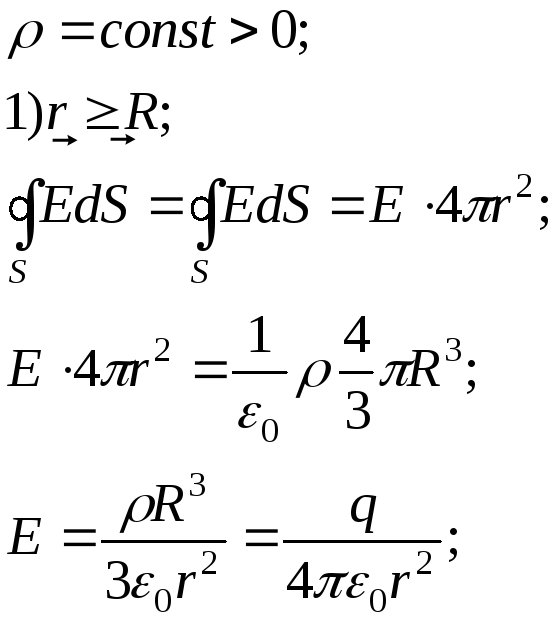
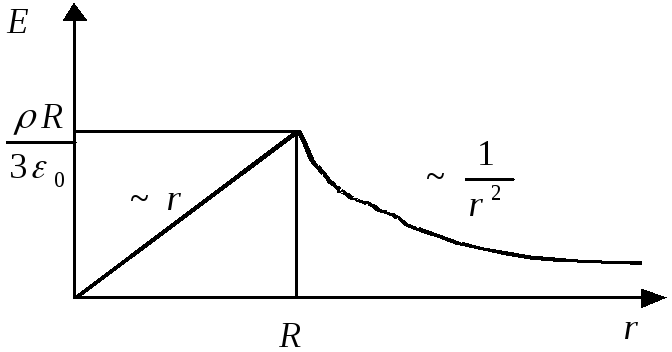
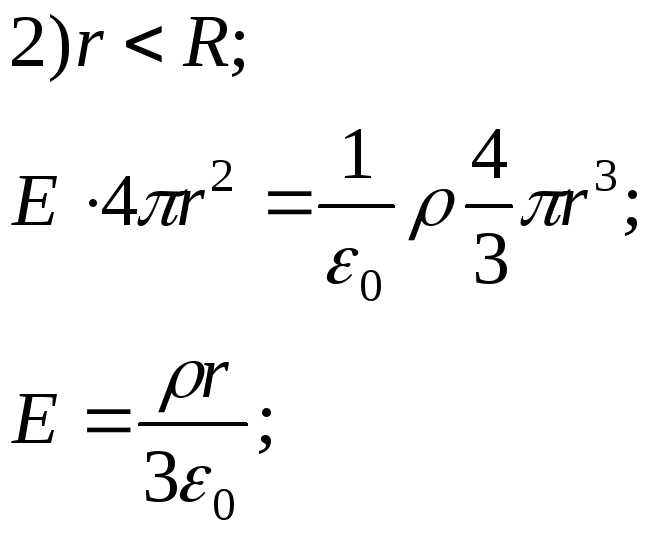
Алгоритм розв’язання основної задачі електростатики:

1) висновок про симетрію поля;

2) вибір вигляду замкненої поверхні;

3) обчислення потоку крізь неї;

4) обчислення повного заряду всередині поверхні;

5) визначення залежності напруженості від відстані.