
- •Общие положения
- •Универсальный стержень (КЭ 10)
- •Специальные конечные элементы (КЭ 51, 53,54,55)
- •РЕШЕНИЕ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ
- •РАСЧЕТ НА ДИНАМИЧЕСКИЕ ВОЗДЕЙСТВИЯ
- •СУПЕРЭЛЕМЕНТНОЕ МОДЕЛИРОВАНИЕ
- •Стержни
- •Плоское напряженное состояние
- •Плиты
- •Оболочки
- •Объемные элементы
- •Загружения
- •РАСЧЕТ НА УСТОЙЧИВОСТЬ
- •РЕШЕНИЕ НЕЛИНЕЙНЫХ ЗАДАЧ
- •Общие положения
- •Расчет физически нелинейных задач
- •Библиотека законов деформирования материалов
- •Типы дробления сечений стержней
- •Типы арматурных включений
- •Библиотека конечных элементов для физически нелинейных задач
- •Стержневые конечные элементы (КЭ 210 и 205)
- •Универсальный стержневой элемент (КЭ - 310)
- •Конечный элемент предварительного натяжения (КЭ 308)
- •Специальные конечные элементы односторонних связей
- •Одноузловой элемент односторонней связи (тип КЭ-261)
- •Двухузловой элемент одностоpонней связи (тип КЭ - 262)
- •Рациональная разбивка на конечные элементы
- •Объединение перемещений
- •Абсолютно жесткие вставки
- •Угол чистого вращения
- •Моделирование податливости узлов сопряжения элементов
- •Моделирование шарниров в стержневых и плоскостных элементах
- •Расчет на заданные перемещения
- •Введение связей конечной жесткости
- •Расчет на температурные воздействия
- •Моделирование предварительного напряжения
- •Учёт прямой и косой симметрии
- •Вычисление коэффициентов постели упругого основания
- •Учет работы конструкций совместно с упругим основанием
- •Расчет оболочек и плит, подкреплённых рёбрами
- •Задание весов масс и динамических воздействий
- •Сбор нагрузок на фундаменты
- •Расчетные сочетания нагрузок
- •Согласованная система координат для пластин
- •ПРИНЦИПЫ АНАЛИЗА РЕЗУЛЬТАТОВ РАСЧЕТА
- •Правила знаков при чтении результатов расчета.
- •Результаты расчета на динамические воздействия
- •Суммарные усилия от динамических воздействий
- •Документирование
- •ЖЕСТКОСТНЫЕ ХАРАКТЕРИСТИКИ ЭЛЕМЕНТОВ
- •ПРОВЕРКА ПРОЧНОСТИ ПО РАЗЛИЧНЫМ ТЕОРИЯМ
- •Главные напряжения
- •КЭ плоской задачи теории упругости
- •КЭ плиты
- •КЭ объемного НДС
- •КЭ оболочки
- •Стержневые КЭ
- •Вычисление эквивалентных напряжений
- •Результаты расчета
- •РАСЧЕТ И ПРОЕКТИРОВАНИЕ СТАЛЬНЫХ КОНСТРУКЦИЙ
- •Назначение и возможности
- •Проектируемые сечения
- •Задание дополнительных данных для расчета
- •Конструктивные и унифицированные элементы
- •Проверки несущей способности элементов
- •Описание алгоритмов
- •Сквозной расчет
- •Локальный расчет
- •Представление результатов расчета
- •ПОДБОР И ПРОВЕРКА АРМИРОВАНИЯ В ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТАХ
- •Армирование стержневых элементов
- •Проверка заданного армирования
- •Армирование пластинчатых элементов
Рис. 9.8.
Рис. 9.9.
9.9Расчет на заданные перемещения
Заданное перемещение в узле задается непосредственно на узел как нагрузка.
Положительная величина перемещения - совпадение с направлением соответствующей локальной оси узла.
Положительная величина заданного поворота - вращение против часовой стрелки, если смотреть с конца соответствующей локальной оси.
Если хотя бы в одном загружении предусматривается расчет на заданные перемещения по какому-либо направлению, то по этому направлению нельзя накладывать связь. В остальных загружениях такая связь может быть наложена программно.
9.10 Введение связей конечной жесткости
Связь конечной жёсткости (или упруго податливая связь) применяется при моделировании упругого основания и любого упругого опирания узлов расчетной схемы. КЭ типа 51, реализующий такой тип связи, является одноузловым, ориентируется относительно осей глобальной системы координат и имеет единичную длину.
Допускается применение этого КЭ и в случае абсолютно жёстких связей, совпадающих с осями глобальной системы координат. При назначении жесткостей необходимо иметь в виду, что большие величины их могут ухудшить точность счета. Поэтому обычно рекомендуется задавать жесткости на 1 -2 порядка больше, чем погонные жесткости
82
примыкающих стержней или цилиндрические жесткости пластин. Вычисленные в результате счета усилия в таких элементах облегчают проверку глобального равновесия схемы.
9.11 Расчет на температурные воздействия
При расчете сооружений на температурные воздействия необходимо учитывать требования соответствующих рекомендаций по расчету сооружений конкретного класса. Так, например, при расчете каркасов следует иметь в виду, что задание температурного воздействия по всем элементам без учета податливости соединений элементов, а также возможных поворотов опор, может привести к чрезмерно завышенным усилиям, особенно в защемлённых стойках.
Если стержень подвержен действию перепада температуры, то более нагретые волокна его сечения сжаты, а менее нагретые - растянуты.
Частный случай, когда температура на верхних (ТВ) и нижних (ТН) волокнах симметричного сечения одинакова по величине и по знаку, то есть ТВ=ТН, вызывает только напряжения растяжения или сжатия, что аналогично равномерному расширению волокон вдоль оси стержня.
Другой частный случай, когда температура на верхних и нижних волокнах симметричного сечения одинакова и противоположна по знаку, т.е. ТВ = −ТН, вызывает только изгибные напряжения.
В общем случае температура в какой-либо точке на расстоянии Ζ от срединной плоскости сечения высотой H:
Т = (ТВ + ТH) /2 + (ТH - ТВ) Z/H.
Для крайних волокон ( Ζ=Η/2 ) симметричного относительно оси Υ1 сечения:
Т = (ТВ + ТH) /2 + (ТH - ТВ) /2.
Первое слагаемое определяет часть температурного воздействия, вызывающего равномерный нагрев сечения. Второе слагаемое определяет изгибные усилия, вызванные температурным перепадом.
При расчете несимметричных сечений величина изгибных напряжений от смещения оси Χ1 по высоте (ширине) сечения не корректируется
Всё сказанное распространяется и на конечные элементы оболочек.
9.12 Моделирование предварительного напряжения
Такое состояние может быть смоделировано при помощи конечного элемента 308 (форкопф) или же при помощи температурного воздействия.
Если величина предварительного напряжения для одиночного стержня известна, можно определить адекватное температурное воздействие на него.
Но для всей конструкции в целом назначить величину температурного воздействия Т для моделирования предварительного напряжения NПН сразу не удастся, так как податливость всех элементов конструкции по заданному направлению ещё не известна.
В качестве первого приближения нужно задать на конструкцию начальную температуру Тн любой величины, выполнить расчет конструкции на эту температуру, получить величину продольного усилия N в напрягаемом элементе, а затем окончательно назначить величину температурного воздействия:
83
Т= ΝΠΗ−Ν Тн
Аналогично решается задача для случая, когда предварительному напряжению подвержено одновременно несколько стержней.
На рис.9.10.а показана расчетная схема фермы, где вводятся три разные величины предварительного напряжения Х1ПН, Х2ПН, Х3ПН в трёх разных стержнях.
Если величина температурного воздействия на первый стержень равна Тн1, то на другие стержни:
Тн2 = |
Χ2ΠΗ |
Тн1; |
Тн3= |
Χ3ΠΗ |
Тн1. |
|
Χ1ΠΗ |
|
|
Χ1ΠΗ |
|
Расчет на заданные температурные воздействия (рис.9.10.б) дает усилия в стержнях соответственно N1, N2, N3. Эти усилия противоположны по знаку усилиям предварительного напряжения.
После определения величины Α = − ΝΠΗΝ1 1 окончательно назначаются необходимые температурные воздействия в стержнях
Т1=А Тн1; Т2=А Тн2; Т3= А Тн3
и окончательно решается задача по схеме (рис.9.10.в), куда добавляются и все другие необходимые загружения.
Усилия в стержнях, напрягаемых температурными воздействиями, противоположны по знаку усилиям от предварительного напряжения, поэтому расчет на заданные температурные воздействия рекомендуется выделять в отдельное загружение. Для остальных элементов конструкции знаки усилий не изменяются.
Если необходимо произвести выбор расчетных сочетаний усилий, рекомендуется:
-загружения температурными воздействиями объявить постоянными; -выделить предварительно напрягаемые элементы в отдельный список для выбора коэффициентов расчетных сочетаний; -по этому списку для загружения температурным воздействием задать коэффициенты со знаком минус.
84
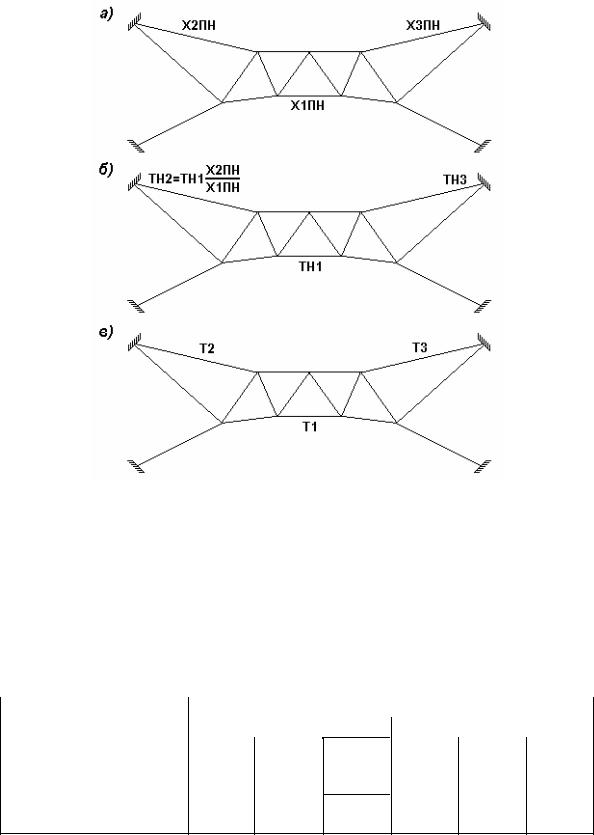
Рис.9.10
9.13 Учёт прямой и косой симметрии
Если рассчитываемая схема имеет плоскости симметрии, то для уменьшения размерности задачи рекомендуется вводить в расчет часть схемы, ограниченную этими плоскостями.
На узлы, лежащие в плоскости прямой симметрии, налагаются связи, ортогональные этой плоскости, а при косой симметрии - параллельные ей. В табл.9.1 показано, по каким направлениям степеней свободы на эти узлы накладываются связи.
|
|
|
|
|
Таблица 9.1 |
|||
|
|
|
Симметрия |
|
|
|
||
|
|
прямая |
|
|
косая |
|
|
|
Плоскости |
|
|
|
|
|
|
|
|
симметрии |
XOZ |
XOY |
YOZ |
XOZ |
XOY |
YOZ |
||
или параллельные ей |
|
|
X,UY, |
|
|
|
|
|
Налагаемые связи |
Y,UX, |
Z,UX, |
X,Z, |
X,Y, |
Y,Z |
|
||
UZ |
UY |
UZ |
UY |
UZ |
UX |
|||
|
||||||||
Если плоскость симметрии не параллельна ни одной из плоскостей общей системы координат, то наложение соответствующих связей можно выполнить с помощью локальной системы координат узла.
Если имеются абсолютно жёсткие связи, не совпадающие с направлением осей общей системы координат, то они реализуются также с помощью локальной системы координат узла.
85
