
otvety / ГОСы современные методы ЖБК
.docxНАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ В ВЕРТИКАЛЬНОМ СЖИМАЮЩЕМ СИЛОВОМ ПОТОКЕ (стадии НДС в сжато-растянутой области)
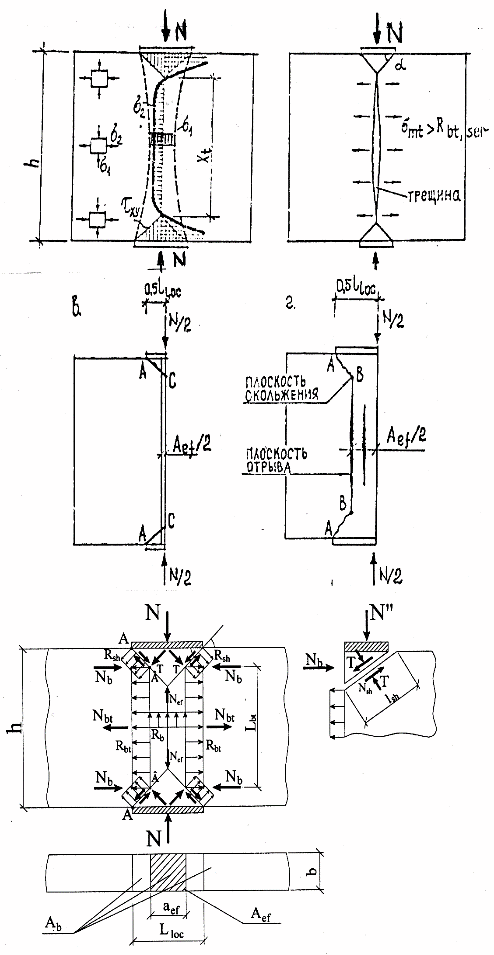
а. эпюры главных напряжений в сжимающем силовом потоке. Стадия 1.
б. появление (стадия 1 ) и развитие трещин (стадия 2) в области сжатия-растяжения.
в. разрушение от сдвига при отношении Lloc /h 0.3. Стадия 3.
г. разрушение от сопротивления отрыву, сдвигу и раздавливанию при Lloc /h > 0.3. Стадия 3.
МОДЕЛЬ РАЗРУШЕНИЯ ПЛОСКО-НАПРЯЖЕННЫХ БЕТОННЫХ ЭЛЕМЕНТОВ ДЛЯ ОЦЕНКИ ПРОЧНОСТИ В СЖИМАЮЩЕМ СИЛОВОМ ПОТОКЕ

Геометрические характеристики.
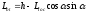
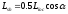
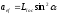
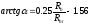 Физические
характеристики.
Физические
характеристики.
Используя метод статический принцип метода предельного равновесия, принимаем в расчетных зонах предельные значения для бетона - Rbt,Rsh,Rb. Тогда внутренние усилия равны:
-
отрыву
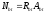
-
сдвигу

-
Раздавливанию
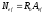
Статические характеристики.
Условие
прочности:
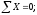
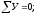
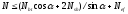
Из
условия прочности:
 где
где
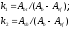
ИСПОЛЬЗОВАНИЕ МОДЕЛИ РАЗРУШЕНИЯ БЕТОНА ДЛЯ ОЦЕНКИ ПРОЧНОСТИ ЭЛЕМЕНТОВ ПРИ «СМЯТИИ»
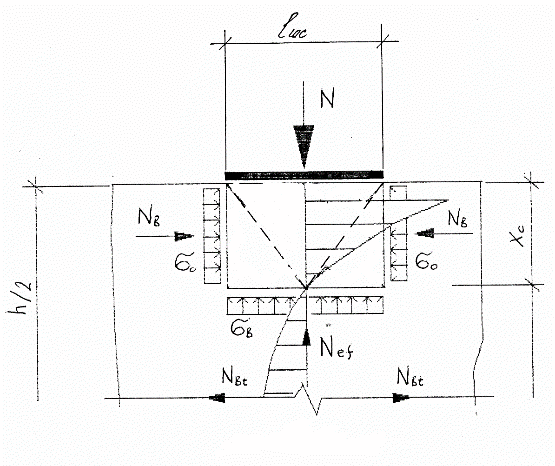
Условие прочности:
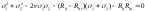
При различных значениях параметра получают все возможные поверхности вращения, характеризующие прочность материала.
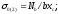





 - находим разрушающую
нагрузку N.
- находим разрушающую
нагрузку N.
ОЦЕНКА ПРОЧНОСТИ И ТРЕЩИНОСТОЙКОСТИ ПЛОСКО-НАПРЯЖЕННЫХ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ НА ОСНОВЕ МОДЕЛИ РАЗРУШЕНИЯ
Стадии напряженно-деформированного состояния
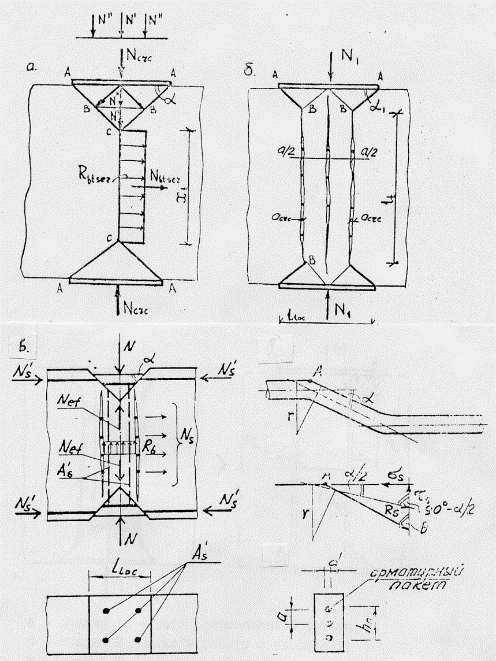
а – стадия 1. Образование трещин;
б – стадия 2. Работа с трещинами;
в – стадия 3. Разрушение.
Расчет по образованию трещин (стадия 1)
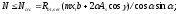
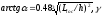 - угол наклона
арматуры к усилию N
- угол наклона
арматуры к усилию N
Расчет по раскрытию трещин (стадия 2)
 - формула проф.
Мурашева
- формула проф.
Мурашева
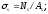
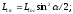
Расчет по прочности (стадия 3)


СЖАТЫЕ ПЛОСКО-НАПРЯЖЕННЫЕ ЭЛЕМЕНТЫ
Расчетные схемы и способы передачи нагрузки
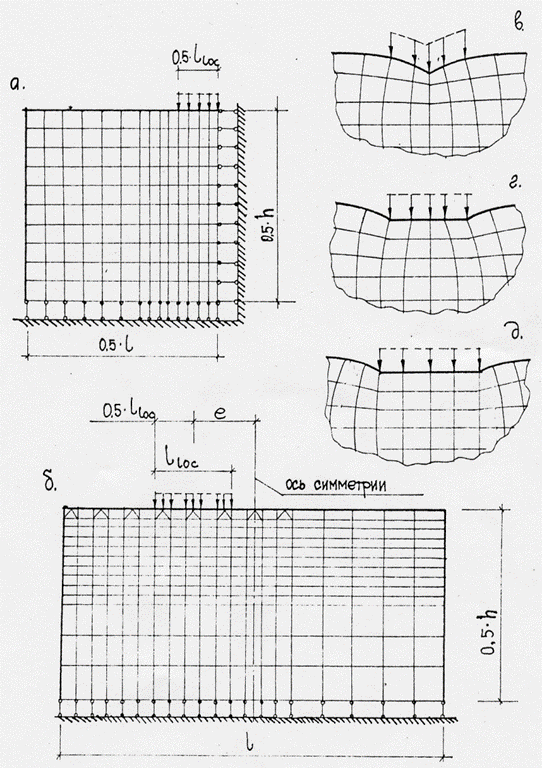
Результаты расчетов с использованием лицензионных ПК «ЛИРА», «ANSYS», «STARK» и др.

Характер распределения напряжений в плоских элементах серий 3(а) и 4 (б)
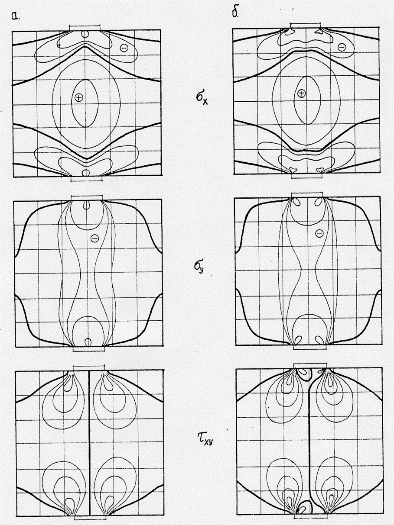
Характер распределения напряжений в
плоских элементах при краевом загружении

ИЗГИБАЕМЫЕ КОРОТКИЕ ВЫСОКИЕ ЭЛЕМЕНТЫ И КОНСТРУКЦИИ
Общий вывод по изучению НДС коротких высоких элементов – в стадии разрушения элементы и конструкции превращаются в распорные системы, работу которых можно представить в виде каркасно-стержневого аналога, состоящего из растянутого пояса (1), сжатых подкосов (2), сжатого горизонтального пояса (3), внешних (4) и внутренних (5) узлов.
Каркасно-стержневые модели балок-стенок

а – при действии сосредоточенных сил;
б – стадии работы арматуры при действии сосредоточенных сил, 1 – при Р = 0.3Рразр., 2 – при Р = 0.6Рразр., 3 – после появления трещины Т-2;
в – при загружении равномерно распределенной нагрузкой.
Определение геометрических размеров каркасно-стержневых аналогов
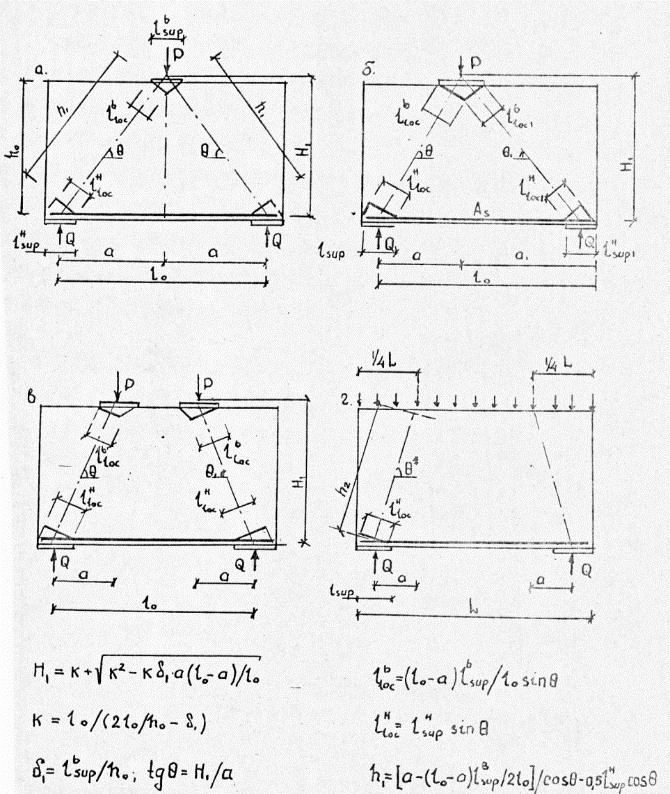
РАСЧЕТ ПО ПРОЧНОСТИ БЕТОННЫХ ЭЛЕМЕНТОВ ЦИЛИНДРИЧЕСКОЙ ФОРМЫ

Определение геометрических характеристик модели разрушения:
 -
угол наклона площадки сдвига;
-
угол наклона площадки сдвига;
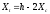 -
расстояние между вершинами конуса
трехосного сжатия;
-
расстояние между вершинами конуса
трехосного сжатия;
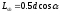 - длина площадки
скольжения;
- длина площадки
скольжения;
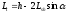 -
высота поверхности отрыва бетона по
боковой поверхности ядра сечения;
-
высота поверхности отрыва бетона по
боковой поверхности ядра сечения;
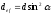 - диаметр ядра
сечения.
- диаметр ядра
сечения.
Условие прочности по общей модели разрушения:
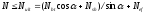
РАСЧЕТ БАЛОК-СТЕНОК РАЗЛИЧНЫХ КОНСТРУКТИВНЫХ РЕШЕНИЙ ПО ПРОЧНОСТИ И ТРЕЩИНОСТОЙКОСТИ С ИСПОЛЬЗОВАНИЕМ КАРКАСНО-СТЕРЖНЕВОГО АНАЛОГА (КСА)
.
Однопролетные балки-стенки со сплошной
стенкой при
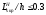

а – развитие трещин в полосе перед разрушением; б, в – расчетные схемы соответственно с наклонными и вертикальными плоскостями сдвига
Однопролетные
балки-стенки со сплошной стенкой при

а – бетонная полоса;
б, в – железобетонная полоса.
Однопролетные балки-стенки со сплошной стенкой при действии равномерно распределенной нагрузки
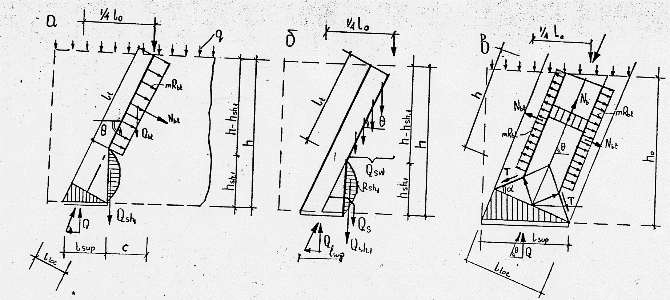
а – без поперечной арматуры;
б
– поперечное армирование,
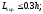
в
– без поперечной арматуры

РАСЧЕТ ПО ПРОЧНОСТИ БАЛОК-СТЕНОК СО СПЛОШНОЙ СТЕНКОЙ
Для подбора продольной арматуры
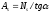 – из равновесия
усилий в опорном узле
– из равновесия
усилий в опорном узле
Оценка прочности бетонных наклонных сжатых полос КСА в общем виде
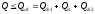
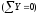
Оценка прочности железобетонных наклонных сжатых полос КСА в общем виде
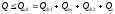
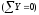
Прочность узлов КСА
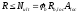
Прочность горизонтальных полос КСА
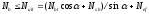
РАСЧЕТ БАЛОК-СТЕНОК РАЗЛИЧНЫХ КОНСТРУКТИВНЫХ РЕШЕНИЙ ПО ПРОЧНОСТИ И ТРЕЩИНОСТОЙКОСТИ С ИСПОЛЬЗОВАНИЕМ КАРКАСНО-СТЕРЖНЕВОГО АНАЛОГА (КСА)
Однопролетные балки-стенки с проемами

а – схема разрушения сжатых полос;
б – расчетная схема разрушения по схеме 3.
Прочность по растянутой зоне:
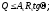
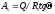
Схема 3 предусматривает возможность разрушения от сдвига бетона по горизонтальному сечению. В этом случае условия равновесия и прочности описываются системой уравнений:

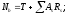
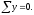
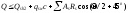
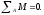

Сопротивление разрушению по горизонтальному сечению происходит за счет работы бетона на сдвиг.
Условие прочности записывается в виде:
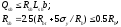
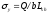 -
вертикальные сжимающие напряжения;
-
вертикальные сжимающие напряжения;
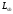 - длина горизонтальной
плоскости сдвига.
- длина горизонтальной
плоскости сдвига.
РАСЧЕТ ПО ПРОЧНОСТИ КАМЕННЫХ И АРМОКАМЕННЫХ КЛАДОК. МЕТОДИКА РАСЧЕТА КАМЕННОЙ КЛАДКИ ИЗ ПУСТОТЕЛЫХ КАМНЕЙ НА ЦЕНТРАЛЬНОЕ СЖАТИЕ
Условие
прочности по общей модели разрушения:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
где р1 - пустотность по горизонтальному сечению камня;
р2 - пустотность по вертикальному сечению камня;
Физическая модель разрушения каменного столба

Физическая модель разрушения каменного столба с косвенным армирование

