информатика1ё / wesna / labor1 / 18в
.doc18 вариант
Составить программу
для вычисления системы линейных
алгебраических уравнений по формулам
Крамера
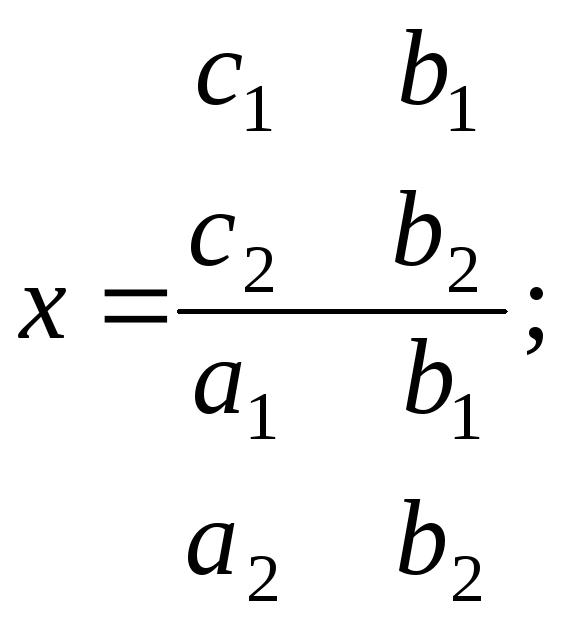
Вычисление
определителей оформить как подпрограмму.
Подпрограмма типа GOSUB
INPUT a1, b1, с1
INPUT a2, b2, с2
u1 = c1: u2 = c2
v1 = b1: v2 = b2
GOSUB 10: t1 = u
u1 = a1: u2 = a2
v1 = b1: v2 = b2
GOSUB 10: t2 = u
X = t1/ t2
u1 = a1: u2 = a2
v1 = c1: v2 = c2
GOSUB 10: t1 = u
v1 = b1: v2 = b2
GOSUB 10: t2 = u
Y = t1/ t2
PRINT X,Y
END
-
u = u1 * v2 – u2 * v1
RETURN
end
Подпрограмма типа FUNCTION
DECLARE FUNCTION SUM (u1, U2, V1, V2)
INPUT a1, b1, с1
INPUT a2, b2, с2
X = SUM (c1, C2, b1, b2) / SUM (a1, a2, b1, b2)
y = SUM (a1, a2, c1, c2) / SUM (a1, a2, b1, b2)
PRINT x,Y
END
FUNCTION SUM (u1, U2, V1, V2)
u = u1 * v2 – u2 * v1
SUM = u
END FUNCTION
Подпрограмма типа SUB
DECLARE SUB SUMMA (u1, u2, V1, V2)
INPUT a1, b1, с1
INPUT a2, b2, с2
CALL SUMMA (c1, C2, b1, b2, u1)
t1 = u1
CALL SUMMA (a1, a2, b1, b2, u2)
t2 = u2
x = t1 / t2
CALL SUMMA (a1, a2, c1, c2, u1)
t1 = u1
CALL SUMMA (a1, a2, b1, b2, u2)
t2 = u2
y = t1 / t2
PRINT “x=”; x; “Y=”; y
END
SUB SUMMA (u1, u2, V1, V2, u)
u = u1 * v2 – u2 * v1
END SUB