
информатика1ё / wesna / MIRONOFF
.DOC
ЛЕКЦИЯ 4. Численные методы линейной алгебры(продолжение)
Итерационные методы решения СЛАУ
Один из методов решения СЛАУ
|
{ |
. (1) .
|
состоит в следующем. Преобразуем систему (1) к виду
|
{ |
|
где буквы![]() и
и
![]() означают новые значения коэффициентов.Это
можно сделать многими способами,например,можно
перенести все члены уравнений (1) в правую
часть и затем прибавить к обеим частям
i-того уравнения неизвестное
означают новые значения коэффициентов.Это
можно сделать многими способами,например,можно
перенести все члены уравнений (1) в правую
часть и затем прибавить к обеим частям
i-того уравнения неизвестное
![]() .
Далее, зададим начальное (нулевое)
приближение корней
.
Далее, зададим начальное (нулевое)
приближение корней
![]()
и построим последовательность приближений по правилу
|
{ |
|
Если существуют пределы
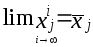 ,
j=1,2,... n, (4)
,
j=1,2,... n, (4)
то они являются
искомыми корнями. Действительно, переходя
в (3) к пределу мы видим, что должны
заменить величинами![]() и числа
и числа![]() в правой части, и
в правой части, и
![]() в левой. Значит, пределы (4) удовлетворяют
СЛАУ (2), а тогда - и эквивалентной системе
(1).
в левой. Значит, пределы (4) удовлетворяют
СЛАУ (2), а тогда - и эквивалентной системе
(1).
Таким образом, мы получили следующий алгоритм:
1. Выбираем начальное (нулевое) приближение.
2. Вычисляем первое приближение, положив в формуле (3) i=0.
3. Вычисляем второе приближение, положив в формуле (3) i=1.
.
.
m. Вычисляем (m+1)-ое
приближение, положив в (3) i=m. Если это
приближение отличается от предидущего
м-того менее чем на e,
где e-
заранее заданная
допустимая погрешность, то мы
останавливаемся и полагаем![]() ,
j=1,2,... n.
,
j=1,2,... n.
Здесь многократно повторяются вычисления по формуле (3). Результат каждого вычисления (левая часть) на следующем шаге подставляется в правую часть в качестве аргумента. Такие вычислительные процессы называются итерационными, а каждый шаг процесса называется итерацией.
Сушествует много итерационных методов решения СЛАУ. Рассмотреный выше метод называется методом простых итераций.
Итерационные методы не являются прямыми, поскольку количество шагов нельзя определить заранее.
В связи с каждым итерационным методом возникают следующие вопросы:
а) при каких условиях метод сходится, т.е. когда мы можем быть уверены в существовании предела (4)?
б) насколько обоснованно правило остановки?
Последний вопрос означает следующее. Вообще говоря, возможжна ситуация, когда m-тое и (m+1) приближенияочень близки между собой, но их отклонение от значения предеоа (4) при этом велико, т.е. наше превило остановки может дать недопустимо большую погрешность. Как обезопасить себя от такой неприятности - вот в чем смыл второго вопроса.
Ответ на эти оба вопроса дает следующий результат весьма общего характера.
Принцип сжатых отображений.
Пусть R есть n-мерное векторное пространство, т.е. множество всех n-мерных векторов u=(u1, u2, ... un). Закон соответствия, связывающий каждый вектор u с некоторым новым вектором v называется отображением пространства на себя. Пишут v=Au, где А обозначение данного отображения. Напомним, что
![]()
Определение. Отображение А называется сжатым, если
![]() (5)
(5)
для любых двух векторов u,v и некоторого не зависящего от них числа q, причем 0<q<1.
Для сжатых отображений легко выясняются все вопросы, касающиеся решения уравнения
xi=Ax (6)
итерационными методами.
Теорема. Если А есть сжатое отображение, то :
1) уравнение (6) имеет единственное решение х*,
2) это решение может быть найдено как предел последовательных приближений, построенных по правилу
хi+1=Axi (7)
где начальное приближение х0 может быть выбрано произвольно,
3) отклонение m-того приближения от точного решения удовлетворяет оценке
![]() /(1-q)
(8)
/(1-q)
(8)
Первые два из этих утверждений часто называют принципом сжатых отображений.
Доказательство.
Обозначим
![]() .
Тогда
.
Тогда
![]() ,
,
![]() и т.д. В итоге получим
и т.д. В итоге получим
![]() (9)
(9)
Очевидно,
xj+i=x0+(x1-x0)+(x2-x1)+....+(xi+1-xi),
т.е. предел последовательности (7) существует, если сходится ряд
![]() (10)
(10)
(сходимость ряда из векторов понимается покоординатно). Но согласно (9) для j -тых координат имеем
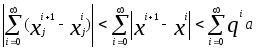 ,
,
и последний ряд сходится, как сумма геометрической прогрессии знаменатель которой меньше единицы. И так, ряд (10) сходится. Значит, предел последовательности (7) существует и равен х0 +s. Но тогда этот предел дает решение уравнения (6). Таким образом, мы доказали, что уравнение (6) разрешимо, и что одно из его решений может быть получено итерационным методом (7). Нам осталось доказать единственность решения и оценку погрешности (8).
Единственность мы докажем от противного. Допустим, что уравнение (6) имеет два решения х и у. Тогода
![]() .
.
Но отсюда
(1-q)![]() <0,
<0,
и, поскольку (1-q)>0,
![]() <0
<0
но это возможно лишь если х=у. Единственность доказана.
Теперь докажем оценку (8). Имеем
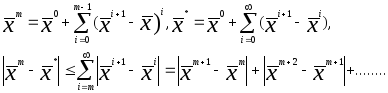
Очевидно,
![]()
и
![]()
Теорема доказана.
Поскольку 1/(1-q)>1, то разность двух последовательных приближений действительно может оказаться меньше реальной погрешности. При вычислениях, требующих высокой точности, мы должны откорректировать правило остановки с учетом формулы (8): останавливаться следует при
![]()
Теперь мы должны выяснить, чему равна характеристика q для СЛАУ. Для этого нам сначала придется получить одно обобщение принципа сжатых отображений.
Нормы векторов.
В этом доказательстве
мы не использовали геометрических
свойств величины
![]() ,
т.е. длины вектора. Нам нужны лишь
несколько алгебраических свойств этой
величины, в первую очередь неравенство
треугольника
,
т.е. длины вектора. Нам нужны лишь
несколько алгебраических свойств этой
величины, в первую очередь неравенство
треугольника
![]()
а также тот факт,
что величина![]() неотрицательна и равна нулю лишь если
вектор x нулевой.
неотрицательна и равна нулю лишь если
вектор x нулевой.
Определение.
Пусть задано
правило, связывающее с каждым вектором
х неотрицательное число
![]() .
Это число называется нормой вектора,
если выполнены три условия:
.
Это число называется нормой вектора,
если выполнены три условия:
1)
![]() тогда и только тогда, когда х=0,
тогда и только тогда, когда х=0,
2) для любых двух
векторов выполнено неравенство ![]()
3) для любого вектора х и любого числа с выполнено равенство
![]()
В частности, нормой является длина. Но существуют и другие векторные нормы. Так, совсем нетрудно показать, что нормой является величина
![]() (11)
(11)
Любая такая норма может быть использована в принципе сжатых отображений. Т.о. справедлива
Теорема.
Пусть для отображения
А можно указать такую векторную норму
![]() что
что
![]()
для любых двух векторов u,w и некоторого фиксированного числа q, причем 0<q<1. Тогда уравнение (6) имеет единственное решение, которое является пределом последовательности (7) при любом начальном приближении, и прогрешность этого итерационного процесса удовлетворяет оценке (8).
Норма матрицы.
С каждой нормой n-мерных векторов можно связать следующую характеристику квадратных матриц размера n на n, также называемую нормой.
Определение.
Пусть
![]()
![]() есть
некоторая векторная норма, а М-квадратная
матрица. Величина
есть
некоторая векторная норма, а М-квадратная
матрица. Величина
max
![]() ,
,
где максимум
берётся по всем векторам e со свойством
![]() ,называется
нормой матрицы М (ассоциированной с
исходной векторной нормой) и обозначается
,называется
нормой матрицы М (ассоциированной с
исходной векторной нормой) и обозначается
![]() .
.
Любой вектор х может быть представлен в виде x=re, где r-его норма, а е-вектор еденичной нормы. Поэтому
![]() ,
,
т.е. для любого
вектора соответствующей размерности
имеем
![]()
Вычисление нормы матрицы , ассоциированной с длиной вектора, довольно громоздко. Гораздо легче вычисляется матричная норма, ассоциированная с векторной нормой (11).
Теорема.Величина
![]() равна наибольшей из сумм абсолютных
величин элементов строк матрицы М.
равна наибольшей из сумм абсолютных
величин элементов строк матрицы М.
Доказательство.Для простоты докажем это при n=2, в общем случае доказательство совершенно аналогично. Пусть
М=( )
)
e=![]() .
Условие
.
Условие
![]() означает, что
означает, что
![]() i=1,2. Но
i=1,2. Но
Me={m11e1+m12e2, m21e1+m22e2}
и![]() max
{
max
{![]() ,
,
![]() }<=
}<=
max {![]()
Пусть, для конкретности, сумма абсолютных величин элементов первой строки больше, чем второй, т. е.
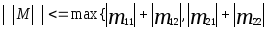 }=
}=![]()
Рассмотрим вектор v={v1, v2}, где v1=+1, если m11 положительно, и
v1=-1,
если m11
отрицательно. Аналогично, v2=+1
или -1 в зависимости от знака m12
. Очевидно,
![]() и
и
![]() .
.
Теорема доказана.
Сходимость метода простых итераций.
Уравнение (2) можно записать в виде (6), где отображение А определяется как
Ах=Мх+В,
где M-квадратная
матрица, составленная из коэффициентов
при неизвестных в правых частях (2), а
В-вектор, составленный из свободных
членов. Для любых двух векторов u,v и для
любой векторной нормы
![]() имеем
имеем
![]() ,
,
т. е. это отображение является сжатым, если
![]() ,
,
где
![]() -
какая-либо норма матрицы М.
-
какая-либо норма матрицы М.
В частности, теперь мы можем сказать, что метод простых итераций сходится, если сумма абсолютных величин коэффициентов при неизвестных в правой части каждого из уровней (2) меньше еденицы. Наибольшая из этих сумм может использоваться в качестве величины q в оценке погрешности (8).
Метод
Гаусса-Зейделя является
усовершенствованием метода простых
итераций, основанным на следующем
замечании. При вычислении очередного
приближения по формуле (3) мы можем
использовать значения
![]() xji
по мере их вычисления, а не дожидаться
следующего (i+1)-го шага. Кроме того, метод
Гаусса-Зейделя предполагают следующий
стандартный путь преобразования системы
(1) к виду (2): в i-ом уравнении мы должны
перенести в правую часть все члены,
кроме aiixi
и поделить
на aii.
Получается система
xji
по мере их вычисления, а не дожидаться
следующего (i+1)-го шага. Кроме того, метод
Гаусса-Зейделя предполагают следующий
стандартный путь преобразования системы
(1) к виду (2): в i-ом уравнении мы должны
перенести в правую часть все члены,
кроме aiixi
и поделить
на aii.
Получается система
|
{ |
x1=(-a12x2-a13x3-...-a1nxn+b1)/a11 x2=(-a21x1-a23x3-...-a2nxn+b2)/a22 (2) ............................................... xn=(-an1x1-an2x2-...-an,n-1xn-1+bn)/ann
|
C учётом связанного выше, формула (3) для вычисления последующих приближений приобретает вид
|
{ |
x1i+1=(-a12xi2-a13xi3-...-a1nxin+b1)/a11 x2i+1=(-a21x1i+1-a23xi3-...-a2nxni+b2)/a22 ..................................................... xni+1=(-an1x1i+1-an2x2i+1-...-an,n-1xn-1i+1+bn)/ann
|
Использование (i+1)-го приближения неизвестного xk при вычислении (i+2)-го приближения для хm при m>k может существенно ускорить сходимость процесса.
Следует, однако, помнить, что метод Гаусса-Зейделя сходится не всегда. Поскольку этот метод есть разновидность метода простых итераций, то для его сходимости достаточно, чтобы норма матрицы, составленная из коэффициентов при неизвестных в правой части (2) была <1. Эта матрица имеет вид
0, -a12/a11,-a13/a11,...,-a1n/a11
a21/a22, 0 -a23/a22,...,-a2n/a22
-a31/a33,-a32/a33, 0 ,...,-a3n/a33
...............................................
-an1/ann,-an2/ann,-an3/ann,..., 0
и мы получаем условие
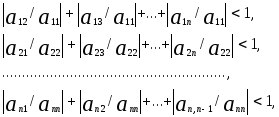
или
![]() k=1,2,...,n.
k=1,2,...,n.
Иначе говоря, для сходимости метода Гаусса-Зейделя достаточно, чтоб
каждый диагональный элемент главной матрицы системы (1) по абсолютной величине превосходил сумму абсолютных величин остальных элементов своей строки. Это условие называется условием доминирования диагонали.
Метод Гаусса-Зейделя очень легко прогаммируетсяю Приведём вариант программы.
10 REM МЕТОД ЗЕЙДЕЛЯ
20 REM ВВОД ИСХОДНЫХ ДАННЫХ
30 DIM A(4,4),B(4),X(4_
40 N=4
51 DATA
52 DATA
53 DATA
54 DATA
60 FOR I=1 TO N
70 FOR J=1 TO N
80 READ A(I,J)
90 NEXT J
100 READ B(I)
110 NEXT I
120 REM КОНЕЦ ВВОДА ИСХОДНЫХ ДАННЫХ
130 FOR I=1 TO N
140 FOR J=1 TO N
150 A(I,J)=A(I,J)/A(I,I)
160 NEXT J
170 B(I)=B(I)/A(I,I)
180 A(I,I)=0
190 NEXT I
200 FOR I=1 TO N
210 FOR J=1 TO N
220 X(I)=B(I)-A(I,J)*X(J)
230 NEXT J
240 PRINT “X(“;I;”)=“;X(I)
250 NEXT I
260 PRINT “ЕСЛИ НУЖНО ПРОДОЛЖАТЬ, ВВЕДИТЕ 1, ЕСЛИ НЕТ- 0”
270 INPUT “ПРОДОЛЖАТЬ” T
280 IF T=1 THEN 200
290 STOP
300 END
Задачи на собственные знания.
Собственное число квадратной матрицы А-это такое число l, для которого можно подобрать такой нулевой вектор х, что
![]() (12)
(12)
Такой вектор х
тоже называют собственным. Если
х-собственный вектор, то сх, где с-любое
нулевое число, также есть собственный
вектор. Действительно, А(сх)=сАх=сlx=l(сх).
Положив с=1/![]() ,
мы получим собственный вектор сх
единичной длины. Такой собственный
вектор называется нормированным.
,
мы получим собственный вектор сх
единичной длины. Такой собственный
вектор называется нормированным.
Из линейной алгебры известно, что все собственные значения (числа) матрицы А=(аij)-есть корни уравнения
det
![]()
 (13)
(13)
Но использование этого уравнения для отыскания собственных значений матрицы обшего вида и высокой размерности приводит к необозримым вычислениям и очень большим погрешностям.
Здесь мы опишем итерационный метод отыскания одного из собственных значений. Он состоит в следующем.
Зададимся начальным
(нулевым) приближением собственного
вектора
![]() Вычислим вектор
Вычислим вектор
![]() и положим l(1)=
и положим l(1)=![]() .
Тогда
.
Тогда
![]()
![]() также
есть 1, т. е.
также
есть 1, т. е.![]() это
нормированный вектор. Далее вычислим
это
нормированный вектор. Далее вычислим
![]() и получим
и получим
![]() Тогда также
Тогда также
![]() .
Продолжая процесс, мы получим
последовательность векторов
.
Продолжая процесс, мы получим
последовательность векторов
![]() и чисел lк,
связанныч соотношением
и чисел lк,
связанныч соотношением
![]() (14)
(14)
Если пределы lim
l(k),
lim
![]() существуют, то
существуют, то
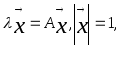
т. е. l-есть собственное значение матрицы А. Можно доказать, что при удачном выборе начального приближения эти пределы существуют, и, что полученное таким образом собственное значение является наибольшим из собственных значений матрицы А.


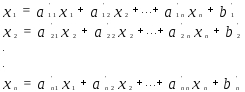 (2)
(2)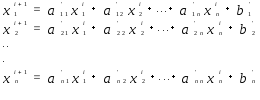 (3)
(3)