Физика - 1 семестр / Физика (молекулярная контрольная)

ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИИЮ ЗАДАЧ И ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ

1.За время изучения курса общей физики студент-заочник должен представить в учебное заведение пять контрольных работ.

2.Номера задач, которые студент должен включить в свою контрольную работу, определяются по таблицам вариантов. Из таблицы 1 решаются задачи, вариант которых совпадает с последней цифрой номера зачетной книжки, из таблицы 2 — задачи, вариант которых совпадает с предпоследней цифрой, и из таблицы 3 — задачи, вариант которых совпадает с третьей справа номера зачетной книжки. Например, номер зачетной книжки 11-04123, тогда из таблицы 1 решаются задачи третьего варианта, из таблицы 2 — второго, и из таблицы 3 — первого.

3.Контрольные работы нужно выполнять чернилами в школьной тетради, на обложке которой необходимо четко привести следующие сведения: фамилию, имя, отчество, факультет, шифр, подробный адрес, номер выполняемой контрольной работы.

4.Условия задач в контрольной работе надо переписать полностью без сокращений. Для замечаний преподавателя на страницах тетради оставлять поля.

5.В конце контрольной работы указать, каким учебником или учебным пособием студент пользовался при изучении физики (название учебника, автор, год издания). Это делается для того, чтобы рецензент в случае необходимости мог указать, что следует студенту изучить для завершения контрольной работы.

6.Высылать на рецензию следует одновременно не более одной работы. Во избежание одних и тех же ошибок очередную следует высылать только после получения рецензии на предыдущую.

7.Если контрольная работа при рецензировании не зачтена, студент обязан представить ее на повторную рецензию, включив в нее те задачи, решения которых оказались неверными. Повторную работу необходимо представить вместе с незачтенной.

8.Зачтенные контрольные работы представляются экзаменатору. Студент должен быть готов во время экзамена дать пояснения по существу решения задач, входящих в контрольные работы.

9.Решения задач следует сопровождать краткими, но исчерпывающими пояснениями; в тех случаях, когда это возможно, дать чертеж выполненный с помощью чертежных принадлежностей.

10.Решать задачу надо в общем виде, т.е. искомую величину в буквенных обозначениях величин, заданных в условии задачи. При таком способе решения не производятся вычисления промежуточных величин.

11.После получения расчетной формулы для проверки правильности ее следует подставить в правую часть формулы вместо символов величин обозначения единиц этих величин, произвести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине.

3

12.Числовые значения величин при подстановке их в расчетную формулу следует выражать только в единицах СИ. В виде исключения допускается выражать в любых, но одинаковых единицах числового значения однородных величин, стоящих в числителе и знаменателе дроби и имеющих одинаковые степени.

13.При подстановке в расчетную формулу, а также при записи ответа числовые значения величин следует записывать как произведение десятичной дроби с одной значащей цифрой перед запятой на соответствующую степень десяти. На-

14. Вычисления по расчетной формуле надо проводить с соблюдением правил приближенных вычислений. Как правило, окончательный ответ следует записывать с тремя значащими цифрами. Это относится и к случаю, когда результат получен с применением калькулятора.

Основы молекулярной физики и термодинамики

Термодинамический метод исследования. Термодинамические параметры. Равновесные состояния и процессы, их изображение на термодинамических диаграммах. Вывод уравнения молекулярно-кинетической теории идеальных газов для давления и его сравнение с уравнением Менделеева–Клапейрона . Средняя кинетическая энергия молекул. Молекулярно-кинетическое толкование термодинамической температуры. Число степеней свободы молекулы. Закон равномерного распределения энергии по степеням свободы молекул. Внутренняя энергия идеального газа. Работа газа при изменении его объема. Количество теплоты. Теплоемкость. Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам и адиабатному процессу идеального газа. Зависимость теплоемкости идеального газа от вида процесса. Классическая мо- лекулярно-кинетическая теория теплоемкостей идеальных газов и ее ограниченность.

Закон Максвелла для распределения молекул идеального газа по скоростям и энергиям теплового движения. Барометрическая формула. Закон Больцмана для распределения частиц во внешнем потенциальном поле. Среднее число столкновений и средняя длина свободного пробега молекул. Время релаксации. Явления переноса в термодинамических неравновесных системах. Опытные законы диффузии, теплопроводности и внутреннего трения. Молекулярнокинетическая теория этих явлений.

Обратимые и необратимые процессы. Круговой процесс (цикл). Тепловые двигатели и холодные машины. Цикл Карно и его КПД для идеального газа. Второе начало термодинамики. Независимость КПД цикла Карно от природы рабочего тела. Энтропия. Энтропия идеального газа. Статистическое толкова-

4

ние второго начала термодинамики. Критика идеалистического толкования второго начала термодинамики.

Отступления от законов идеальных газов. Реальные газы. Силы и потенциальная энергия молекулярного взаимодействия. Эффективный диаметр молекул. Уравнение Ван-дер-Ваальса. Сравнение изотерм Ван-дер-Ваальса с экспериментальными. Фазовые переходы I и II рода. Критическое состояние. Внутренняя энергия реального газа. Особенности жидкого и твердого состояния вещества.

Основные формулы

Количество вещества тела (системы)

ν = N / N A ,

где N — число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему), N A — постоянная Авогадро

( N A = 6.02 1023 моль–1).

Молярная масса вещества

M = m / ν ,

где m — масса однородного тела (системы), ν — количество вещества этого тела.

Относительная молекулярная масса вещества

Mr = ∑ni Ar,i ,

где ni — число атомов i-го химического элемента, входящих в состав молекулы данного вещества, Ar,i — относительная атомная масса этого элемента.

Относительные атомные массы приводятся в таблице Менделеева Д.И.

Связь молярной массы М с относительной молекулярной массой вещества

M = Mr k ,

где k = 10–3 кг/моль.

Количество вещества смеси газов

или

ν= m1 + m2 +L+ mn ,

M1 M2 Mn

5

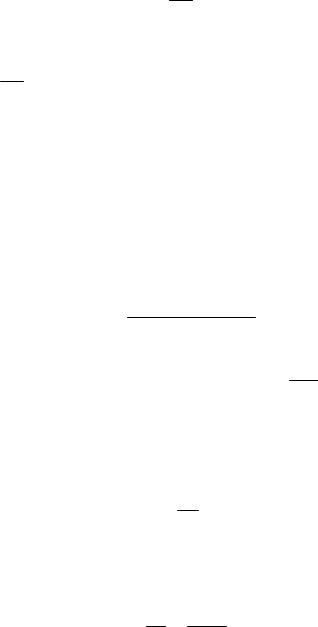
где v, Ni ,mi , Mi — соответственно количество вещества, число молекул, масса, молярная масса i -го компонента смеси.

Уравнение Менделеева–Клапейрона (уравнение состояния идеального

газа)

pV = Mm RT ,

где m — масса, М — молярная масса газа, R — универсальная газовая постоян-

ная, ν = Mm — количество вещества, T — термодинамическая температура.

Закон Дальтона, определяющий давление смеси газов p = p1 + p2 +L+pn ,

где pi — парциальные давления компонентов смеси, n — число компонентов

смеси.

Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.

Молярная масса смеси газов

M = m1 +m2 +L+mn ,

ν1 + ν2 +L+νn

где mi — масса i-го компонента смеси, νi = mi — количество вещества

Mi

i-го компонента смеси, n — число компонентов смеси.

Массовая доля i-го компонента смеси газа (в долях единицы или процен-

тах)

ω = mmi ,

где m -масса смеси. Концентрация молекул

n = VN = NMAρ ,

где N — число молекул, содержащихся в данной системе, ρ — плотность вещества, V — объем системы.

Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.

Основное уравнение кинетической теории газов

6

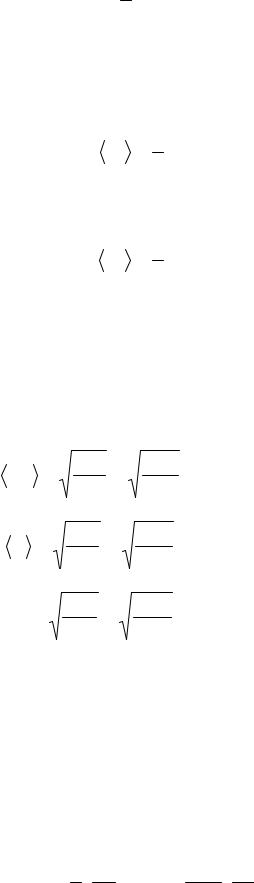
p = 23 n < εn > ,

где < εn > — средняя кинетическая энергия поступательного движения молекулы.

Средняя кинетическая энергия поступательного движения молекулы

εn = 23 kT ,

где k — постоянная Больцмана.

Средняя полная кинетическая энергия молекулы

εn = 2i kT ,

где i — число степеней свободы молекулы. Для одноатомного газа i=3, для двухатомного газа i=5, для многоатомного газа i =6.

Зависимость давления газа от концентрации молекул и температуры p = nkT .

где m — масса одной молекулы.

Относительная скорость молекулы

U =V / Vв,

где V — скорость данной молекулы.

Удельные теплоемкости газа при постоянном объеме ( cv ) и постоянном давлении ( cp )

cv = 2i MR , cp = i +2 2 MR .

7

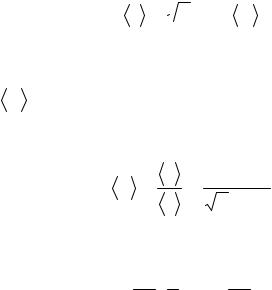
Связь между удельной c и молярной C теплоемкостями

Уравнение Майера

Cp −Cv = R ,

где Cp и Cv — молярные теплоемкости при постоянном объеме и постоянном давлении, соответственно.

Среднее число столкновений молекулы за 1 секунду z = 2πσ2n V ,

где n — концентрация молекул,

σ— эффективный диаметр молекулы,

V — среднеарифметическая скорость молекулы.

Средняя длина свободного пробега молекул газа

λ = vz = 2πσ1 2n .

Внутренняя энергия идеального газа

U = Mm 2i RT = Mm Cv T .

Первое начало термодинамики

Q = U + A ,

где Q — теплота, сообщенная системе (газу), U — изменение внутренней энергии системы, A — работа, совершенная системой против внешних сил.

Работа расширения газа:

8

— при адиабатном процессе, где γ = cp — показатель адиабаты. cv

Уравнение Пуассона, связывающие параметры идеального газа при адиабатном процессе (различные формы записи):

Термический КПД цикла

η= Q1 −Q2 ,

Q1

где Q1 — теплота, полученная рабочим телом от теплопередатчика, Q2 — теплота, переданная рабочим телом теплоприемнику.

Термический КПД цикла Карно

η= T1 −T2 ,

T1

где T1 и T2 — термодинамические температуры теплоотдатчика и теплоприемника.

9