II. Расчеты на удар тел
Продолжительность удара очень мала и сложно вычислить ускорения частиц ударяемой конструкции. Поэтому, воспользоваться принципом ДАламбера затруднительно и обычно здесь используют закон сохранения энергии.
Для удобства
расчета на удар вводят условное понятие
динамическая
сила
![]() .
Эта такая сила, которая, будучистатически
приложенной в точке удара, вызовет такие
же перемещения (деформации) ударяемого
тела, как и при ударе.
.
Эта такая сила, которая, будучистатически
приложенной в точке удара, вызовет такие
же перемещения (деформации) ударяемого
тела, как и при ударе.
Расчет на удар без учета массы ударяемого бруса
Рассмотрим
закрепленный упругий брус, на который
с высоты
![]() падает груз весом
падает груз весом![]() .
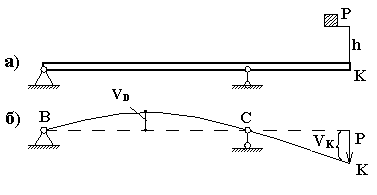
При этом брус может испытывать: а)
продольные деформации (колонны, сваи)
рис. 9.1а, б) изгибные деформации (балки)
рис. 9.1б.
.
При этом брус может испытывать: а)
продольные деформации (колонны, сваи)
рис. 9.1а, б) изгибные деформации (балки)
рис. 9.1б.
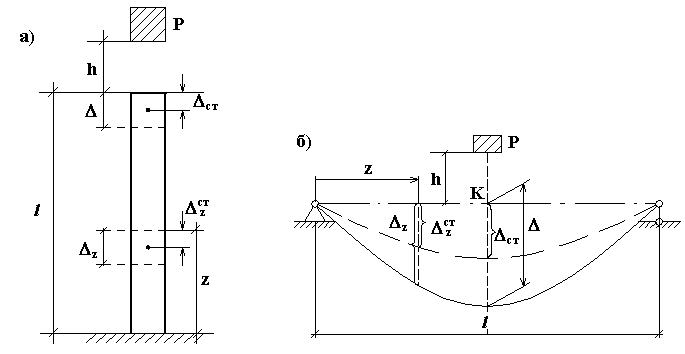
Рис. 9.1
После удара, когда
груз
![]() останавливается в нижнем положении,
деформации каждого сечения бруса
достигают наибольших значений. Их
обозначим:
останавливается в нижнем положении,
деформации каждого сечения бруса
достигают наибольших значений. Их
обозначим:![]() деформации
в точке удара,
деформации
в точке удара,![]() в любом сечении бруса с координатой
в любом сечении бруса с координатой![]() (на рис. 9.1б в эти деформации (прогибы)
показаны сплошной линией). Затем
происходят затухающие колебания бруса,
в конце которых устанавливаются
деформации
(на рис. 9.1б в эти деформации (прогибы)
показаны сплошной линией). Затем
происходят затухающие колебания бруса,
в конце которых устанавливаются
деформации![]() (в точке удара) и
(в точке удара) и![]() в любом сечении, соответствующие
статическому действию груза
в любом сечении, соответствующие
статическому действию груза![]() (на рис. 9.1б эти деформации показаны
пунктирной линией).
(на рис. 9.1б эти деформации показаны
пунктирной линией).
Расчет проведем при следующих допущениях:
Брус идеально упругий, справедлив закон Гука, модуль
 одинаков при динамическом и статическом
нагружении;
одинаков при динамическом и статическом
нагружении;Массу ударяемого бруса пока не учитываем;
Эпюра перемещений сечений бруса от удара подобна эпюре перемещений от статического действия груза
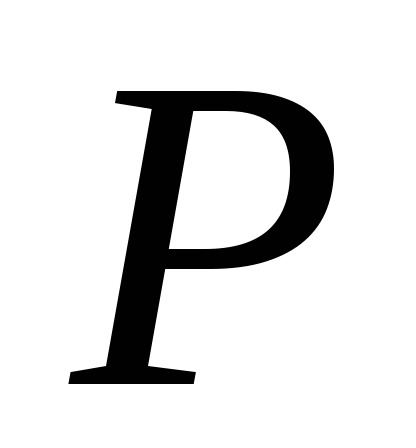 .
(На рис. 9.1б графики прогибов, обозначенные
сплошной и пунктирной линиями, подобны).
Обозначим
.
(На рис. 9.1б графики прогибов, обозначенные
сплошной и пунктирной линиями, подобны).
Обозначим
![]() динамический
коэффициент
(9.3)
динамический
коэффициент
(9.3)
Из третьего допущения и рис. 9.1б следует с учетом (9.3)
![]() (9.4)
(9.4)
Согласно принятого
выше определения динамической силы
![]() ,
от ее статического приложения возникнут
деформации
и
,
от ее статического приложения возникнут
деформации
и
![]() ,
а от статического нагружения силой
,
а от статического нагружения силой![]() появятся
появятся![]() и
и![]() .
По закону Гука деформации пропорциональны
нагрузкам, поэтому
.
По закону Гука деформации пропорциональны
нагрузкам, поэтому
![]() (6)
(6)
По закону Гука и напряжения пропорциональны нагрузкам
![]() (9.5)
(9.5)
Здесь
![]() динамические напряжения, т.е. возникают
в брусе при ударе;
динамические напряжения, т.е. возникают
в брусе при ударе;![]() статические напряжения, возникают при
статическом нагружении силой
статические напряжения, возникают при
статическом нагружении силой![]() .
.
Из (9.4) и (9.5) следует
![]() (9.6)
(9.6)
Итак, деформации
и напряжения в любом сечении бруса при
ударе можно определить по (9.6), если
вычислить
![]() динамический коэффициент. А деформации
динамический коэффициент. А деформации![]() и напряжения
и напряжения![]() при любом виде статической нагрузки
(осевой, изгибной, кручении и т.д.) мы
умеем определять из вышеприведенных
разделов.
при любом виде статической нагрузки
(осевой, изгибной, кручении и т.д.) мы
умеем определять из вышеприведенных
разделов.
Для решения задачи
используем закон сохранения энергии.
Груз
![]() при падении проходит путь
при падении проходит путь![]() и совершает работу
и совершает работу![]() .
.
При статическом
нагружении силой
![]() получим ту же деформацию, что и при
ударе, потенциальная энергия деформации
бруса при этом, как известно, определяется
так
получим ту же деформацию, что и при
ударе, потенциальная энергия деформации
бруса при этом, как известно, определяется
так![]() .
Сила
.
Сила![]() прикладывается в т.К,
куда падает груз
прикладывается в т.К,
куда падает груз
![]() .
По закону сохранения энергии
.
По закону сохранения энергии![]() ,
т.е.
,
т.е.
![]() (7)
(7)
Из (6)
![]() ,
подставим в (7) получим
,
подставим в (7) получим
![]() (8)
(8)
Сокращаем на
![]() и учитывая из (9.4), что
и учитывая из (9.4), что![]() найдем
найдем
![]() или
или ![]() (9)
(9)
Относительно
неизвестной
![]() получили стандартное квадратное
уравнение типа
получили стандартное квадратное
уравнение типа![]()
Здесь
![]() .
Решение квадратного уравнения известно
из справочников:
.
Решение квадратного уравнения известно
из справочников:![]() .
В нашем случае получим
.
В нашем случае получим
![]() (10)
(10)
При ударе всегда
![]() ,
поэтому выбираем знак (+) и формулу (10)
преобразуем так
,
поэтому выбираем знак (+) и формулу (10)
преобразуем так
![]() или окончательно
или окончательно
![]() (11)
(11)
Согласно (9.4)
![]() ,
тогда из (11) получим
,
тогда из (11) получим
![]() (9.8)
(9.8)
Величина ст
статическая деформация бруса в точке
удара от статического приложения силы
![]() в точке «K»
падения груза весом
в точке «K»
падения груза весом
![]() .
Определяется известными методами:
.
Определяется известными методами:
Рис. 9.1а: По закону Гука при осевой нагрузке
![]()
Рис. 9.1б: ![]() прогиб балки в т.
K
от силы
прогиб балки в т.
K
от силы
![]() ,
приложенной в т.K.
Определяется известным методом Клебша
из раздела «Плоский изгиб балок».
,
приложенной в т.K.
Определяется известным методом Клебша
из раздела «Плоский изгиб балок».
Скорость груза,
падающего с высоты
![]() ,
как известно, определяется так
,
как известно, определяется так![]() ,
откуда
,
откуда![]() .
Подставим это в (9.8) получим
.
Подставим это в (9.8) получим
![]() (9.9)
(9.9)
Преобразуем
![]() так:
так:
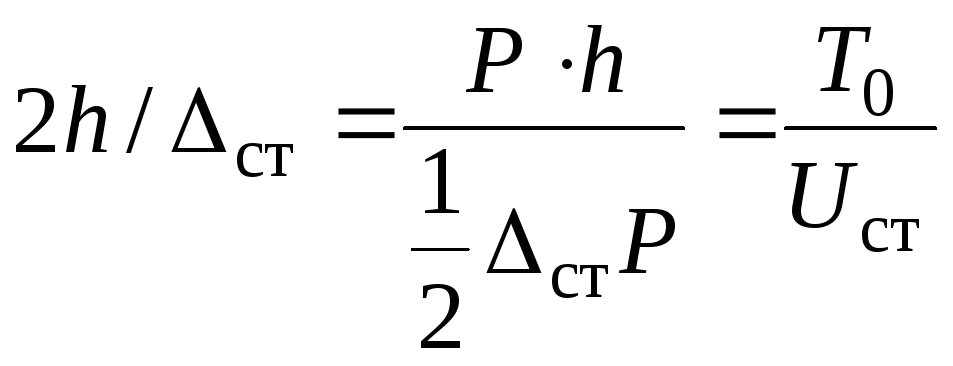 (12)
(12)
Здесь:
![]() энергия падающего груза в момент начала
удара;
энергия падающего груза в момент начала
удара;
![]() потенциальная
энергия деформации бруса от статического
нагружения его силой
потенциальная
энергия деформации бруса от статического
нагружения его силой
![]() в т.K.
в т.K.
С учетом (12) из (9.8) найдем
![]() (9.10)
(9.10)
Из (9.8) следует, что
чем больше
![]() ,
т.е. чем больше деформируется брус от
статической нагрузки
,
т.е. чем больше деформируется брус от
статической нагрузки![]() ,
тем меньше
,
тем меньше![]() и по (9.6) меньше напряжения при ударе.
Так появилась идея ставить в конструкциях,
испытывающих ударные нагрузки, различные
амортизаторы, рессоры, пружины и
поясняется поговорка «знал бы, где
упаду, подстелил бы солому».
и по (9.6) меньше напряжения при ударе.
Так появилась идея ставить в конструкциях,
испытывающих ударные нагрузки, различные
амортизаторы, рессоры, пружины и
поясняется поговорка «знал бы, где
упаду, подстелил бы солому».
Пример. Порядок расчета балки на удар.
|
P |
На балку с высоты
В т. K балки статически при- |
кладываем силу
![]() ,
равную весу груза (рис.б). Определяем от
нее опорные реакции и строим эпюру
,
равную весу груза (рис.б). Определяем от
нее опорные реакции и строим эпюру![]() изгибающих
моментов. Из Эп.
изгибающих
моментов. Из Эп.![]() находим
находим![]() и, зная размеры и форму поперечного
сечения балки, вычисляем
и, зная размеры и форму поперечного
сечения балки, вычисляем![]() максимальные напряжения от статического
нагружения. Для вычислений по (9.6) надо
знать
максимальные напряжения от статического
нагружения. Для вычислений по (9.6) надо
знать![]() .
.
Для балки б) со
статической силой
![]() для двух участков запишем дифференциальные
уравнения изгиба
для двух участков запишем дифференциальные
уравнения изгиба![]() по методу Клебша, интегрируем их и из
условий закрепления балки находим
константы интегрирования. Строим график
прогибов балки, приблизительный вид
которого показан на рис.б. Находим
по методу Клебша, интегрируем их и из
условий закрепления балки находим
константы интегрирования. Строим график
прогибов балки, приблизительный вид
которого показан на рис.б. Находим![]() прогиб балки в сечении «K»,
это и есть
прогиб балки в сечении «K»,
это и есть
![]() .
По (9.8) вычисляем
.
По (9.8) вычисляем![]() и далее
и далее
![]()
В консоли максимальный
прогиб при ударе
![]() .
.
В пролете находим
![]() максимальный прогиб от статического
нагружения и далее максимальный прогиб
при ударе
максимальный прогиб от статического
нагружения и далее максимальный прогиб
при ударе![]() .
.
Дальше можно проверить балку на прочность и жесткость обычными методами.
Существует термин
«падение с высоты
![]() ».
Из (9.8) в этом случае получим
».
Из (9.8) в этом случае получим![]() .
Чтобы этого не было, груз надо опускать
плавно не только до соприкосновения с
конструкцией, но и дальше, при перемещении
груза вместе с деформируемой конструкцией
до полной их остановки.
.
Чтобы этого не было, груз надо опускать
плавно не только до соприкосновения с
конструкцией, но и дальше, при перемещении
груза вместе с деформируемой конструкцией
до полной их остановки.
Учет массы ударяемого тела (бруса)
Учет массы ударяемого тела достаточно сложен, поэтому приведем окончательные формулы без вывода их.
Динамический коэффициент в этом случае определяется по формулам, аналогичным (9.8)-(9.10)
![]() (9.11)
(9.11)
Здесь:
![]() ;
;
![]() вес ударяемого тела, для бруса
вес ударяемого тела, для бруса![]()
![]() редукционный
коэффициент, определяется так
редукционный
коэффициент, определяется так
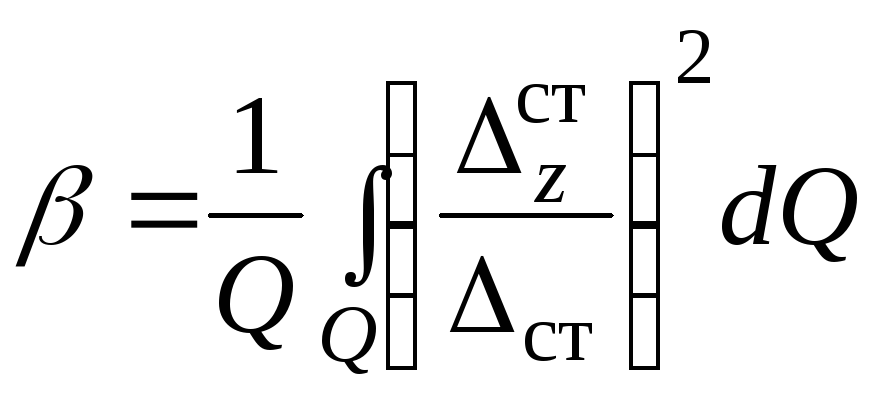 ,
для бруса
,
для бруса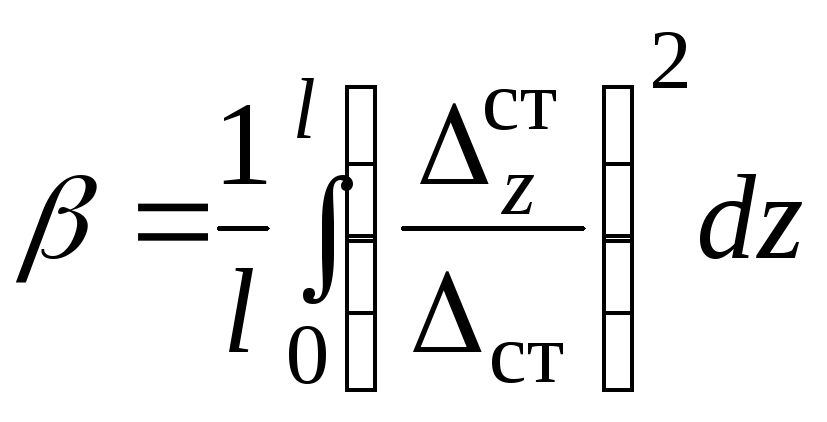 (9.12)
(9.12)
Вычислив
![]() ,
определяем коэффициент
,
определяем коэффициент![]() и далее
и далее![]() .
.
Пример 1.
Вычислить
![]() для колонны, показанной на рис. 9.1а. По
закону Гука для сечения
для колонны, показанной на рис. 9.1а. По
закону Гука для сечения![]() от статического нагружения силой
от статического нагружения силой![]() :
:![]() ,
,![]() ,
где
,
где![]() площадь поперечного сечения колонны,
площадь поперечного сечения колонны,![]() модуль упругости материала.
модуль упругости материала.
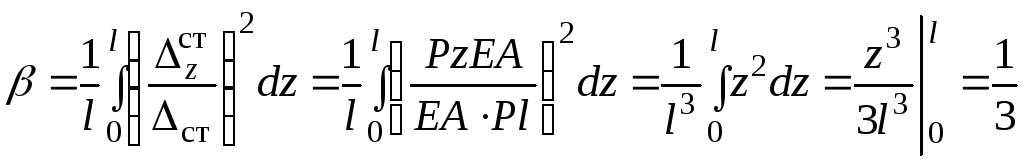 .
.
Пример 2.
Вычислить
![]() для балки, показанной на рис. 9.1б, когда
груз
для балки, показанной на рис. 9.1б, когда
груз![]() падает на середину балки.
падает на середину балки.
Опорные реакции
![]() ,
дифференциальные уравнения изгиба
балки от статического нагружения силой
,
дифференциальные уравнения изгиба
балки от статического нагружения силой![]() :
:
![]() ,
,
т.е. ввиду симметрии ограничимся одним участком.
Граничные условия:
1)
![]() ;
2)
;
2)![]() (ввиду симметрии), откуда найдем
(ввиду симметрии), откуда найдем![]() .
Тогда
.
Тогда![]() ,
т.к.
,
т.к.![]() ,
то
,
то![]() ,
а
,
а![]() ,
,
подставим
![]() получим
получим![]() :
:
![]() ; Найдем
; Найдем
![]()
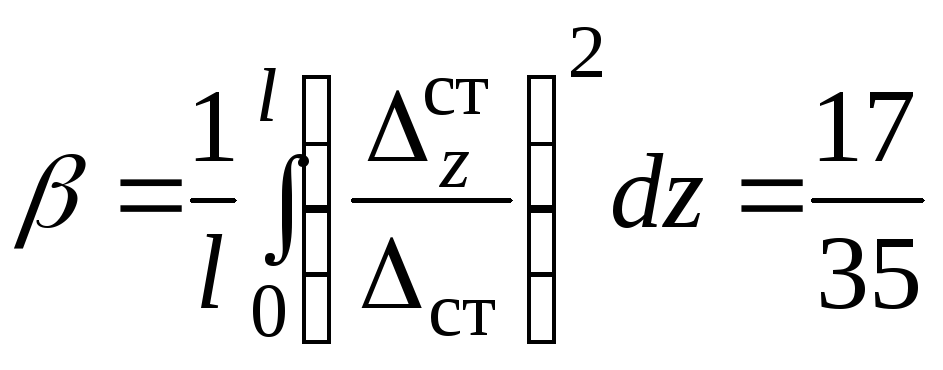 .
.
Все полученные выше формулы приближенные. Чем большей жесткостью обладает ударяемый брус, тем менее точными будут результаты расчетов. Более точные результаты получаются при рассмотрении волновой теории удара.