- •КазанСкий государственный архитектурНо-строительный университет
- •Порядок выполнения
- •Задачи ДлЯ контрольных работ контрольная работа №1
- •VI VII VIII IX X
- •VI VII VIII
- •Контрольная работа №2
- •VI VII VIII IX X
- •Решение
- •Пример к ЗадаЧе 1.2
- •Пример к задаче 1.3.
- •1 Участок: 0 z1 1,5 м
- •2 Участок: 1,5 z2 3,3 м
- •3 Участок: 3,3z3 4,9 м
- •4 Участок: 4,9 z4 6,4 м
- •Контрольная работа № 2
- •Решение
- •Пример задаче 2.2
- •Решение
- •Пример к задаче 2.3.
- •Решение
- •1 Участок 0 z l1
- •1 Участок 0 z l1
VI VII VIII IX X
Рис. 2.1
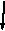
 M
P q P q
M
P q P q




































I
II

 P q M q M
P q M q M







































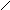
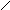






III IV


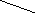
 M P q
P q
M P q
P q














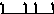







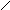




V VI



 q
P M P q M
q
P M P q M






































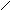



VII VIII

 q
M M q
q
M M q














































P P
IX X





 a b c a b c
a b c a b c


Рис. 2.2

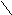 q q
M
q q
M

P
I
II
M q q















P
III IV
q M q























P
V
VI
M q q
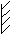




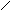

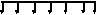




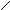
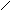


P
VII VIII

P q M q





























 IX
X
IX
X


l
l
l
l

 l
l
l
l
Рис. 2.3
ПРИМЕРЫ ВЫПОЛНЕНИЯ КОНТРОЛЬНЫХ РАБОТ
КОНТРОЛЬНАЯ РАБОТА № 1
ПРИМЕР К ЗАДАЧЕ 1.1
Стальная колонна (Е = 2104 кН/см2) находится под действием продольной силы Р = 20 кН и собственного веса ( = 78 кН/м3).
Требуется:
1. Построить эпюры продольных усилий и нормальных напряжений.
2. Определить опасное сечение и проверить прочность колонны при [] = 16 кН/ см2.
3. Определить перемещение верхнего среза колонны без учета собственного веса.
|
Р а 2A
b A
c 2A
Рис.1
|
Исходные данные: А=10 см2 ; a=2 м; b=1м; с=3м; Р=20 кН. |
Решение
Расчетная схема колонны (Рис.2 ) - ступенчатый брус, загруженный заданной сосредоточенной силой Р и распределенной нагрузкой q1, q2, q3 от собственного веса, где
q1 = А1 = 2А = 782010-4 = 0.156 кН/м;
q2 = А2 = А =781010-4 = 0.078 кН/м;
q3 = А3 = 2А =782010-4 = 0.156 кН/м.
R - опорная реакция.
N, кн , кн/см2
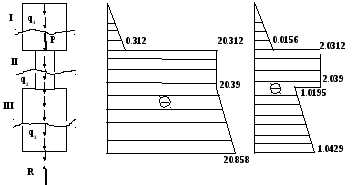 Рис.
2
Рис.
2
Разбиваем
стержень на участки, начиная с верхнего
свободного конца. Границами участков
служат сечения в которых приложены
внешние силы или же изменяется площадь
поперечного сечения. В данном случае
имеем три участка, площади поперечного
сечения которых: А1 =2А=20
см2,
А2=А=10см2,
А3=2А=20см2.
Ось z
направляем вдоль оси стержня от верхнего
среза колонны. Для каждого участка
находим внутренние продольные силы
NZ
методом сечений из условия равновесия
отсеченной верхней части (при этом
отпадает необходимость в определении
реакции заделки R).
Нормальные напряжения z.=![]()
1-ый участок 0 z1 a


 0
z1
2
0
z1
2


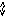

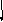
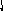 q1
z1
q1
z1
![]()
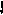
 Nz1
Nz1
![]()
z
![]()





 2
-ой
участок
a
z 2
a+b
2
-ой
участок
a
z 2
a+b
2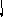
z2
3
z2
3
a q1
z2
q1
z2
![]()



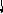 P
P
![]()


 q2
q2
![]()
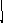 Nz2
Nz2
![]()
z
3

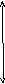


 -ий
участок
a+
b
z3
a+b+c
-ий
участок
a+
b
z3
a+b+c
 3
z
3
6
3
z
3
6
 a
q1
a
q1
![]()


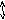
 P
z3
P
z3
![]()





 b
q2
b
q2
![]()



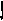 q3
q3
![]()
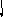 Nz3
Nz3
z
Зависимости NZ и Z линейно зависят от z. Для построения эпюр достаточно вычислить их значения на границах участков. Эпюры NZ и Z строим рядом с расчетной схемой (рис. 2). Ось абсцисс графиков проводим параллельно оси бруса. По оси ординат откладываем в выбранном масштабе значение продольной силы NZ или нормального напряжения Z соответственно. Указываем знак. Штриховка должна быть перпендикулярна оси.
2.
По эпюре нормальных напряжений Z
определяем опасное сечение. Опасное
сечение - сечение в котором
![]() .
.![]() = 2.039 кН/см2.
В опасном сечении записываем условие
прочности при растяжении-сжатии:
= 2.039 кН/см2.
В опасном сечении записываем условие
прочности при растяжении-сжатии:
![]() ,
,
![]()
![]() кН/см2
кН/см2
![]() =2.039
кН/см2
16 кН/см2
. Условие прочности выполняется.
=2.039
кН/см2
16 кН/см2
. Условие прочности выполняется.
3. Результаты расчета показывают, что собственный вес колонны мал по сравнению с приложенной нагрузкой Р. Поэтому при определении перемещения l верхнего среза стальной колонны собственный вес не учитываем. По закону Гука для растяжения-сжатия:
![]()
Определяем l как сумму удлинений ( укорочений ) отдельных участков.
![]()
Без учета собственного веса (q1 = 0, q2 = 0, q3 = 0)

Отрицательное значение l показывает, что колонна укоротилась.