Кручение прямоугольных сечений

Полученные формулы для открытого контура сечения можно применить и для прямоугольного сечения. Если , то формулы (6.10) и (6.11) дают точное решение, т.к. они получены при допущении, что . На рис. показана эпюра в точках сечения у верхней поверхности, аналогична и на нижней поверхности сечения. В углах сечения , а на

большей части размера «b» 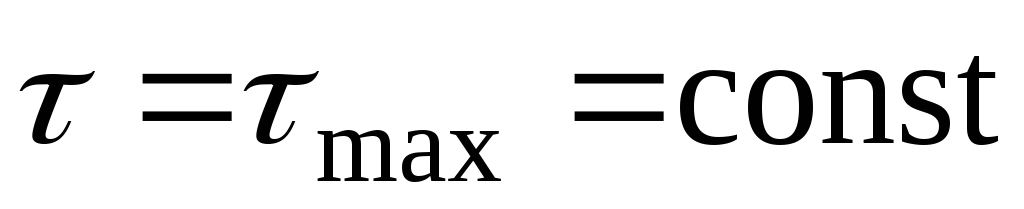. По толщине «» меняются по линейному закону, в точках срединной линии (пунктир) .

Если , то будут переменны по размеру «b», будет в середине длинной стороны, а в углах . Здесь можно использовать формулы:

(6.12)

Здесь: геометрический момент сопротивления, геометрический момент инерции.

Коэффициенты и зависят от отношения и приводятся в справочниках. При , т.е. получаются формулы (6.10) и (6.11).

Кручение тонкостенных профилей

Рассмотрим кручение стержня двутаврового поперечного сечения, показанного на рис. Такое сечение можно разбить на прямоугольники с размерами и . Максимальные будут возникать в точках сечения у

поверхностей в середине каждой длинной стороны «» прямоугольников и вычисляются по формуле (6.13) При кручении форма поперечного сечения не меняется, т.е. все прямоугольники закручиваются одина-ково, относительный угол закручивания всего сечения определяется так (6.14)

В формулах (6.13) и (6.14) вычисляется суммированием по всем прямоугольникам сечения.

(6.15)

Аналогично рассчитываются сечения типа швеллера, уголка и др. Для стандартных профилей в (6.15) введен коэффициент коэффициент формы. для двутавров, для швеллеров.

93