Примеры решения задач
1.
Найти скалярное произведение векторов
и
.
Решение: По формуле (5.3) находим:
.
2.
Векторы
образуют угол
.
Зная, что
,
вычислить
.
Решение: Используя свойства скалярного произведения и формулу (5.1), получаем:
.
3.
Даны вершины треугольника
.
Найти: а) внутренний угол при вершинеC;
б)
.
Решение:
а) Угол
при вершинеC
есть угол между векторами
и
.
Определим координаты этих векторов:
,
.
Найдем
их модули:
;
.
Согласно формуле (5.4)
;
.
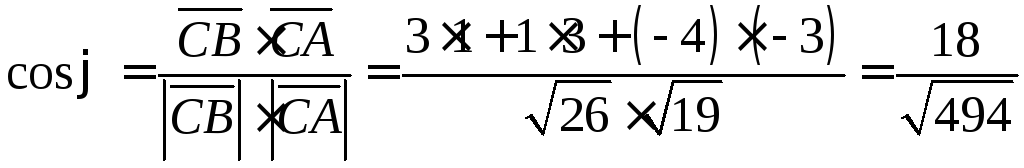б)
Из первого свойства скалярного
произведения получаем 
.Поэтому
=
.
4.
Найти векторное произведение векторов
и
.
Решение: Имеем по формулам (5.6) и (5.7)
.
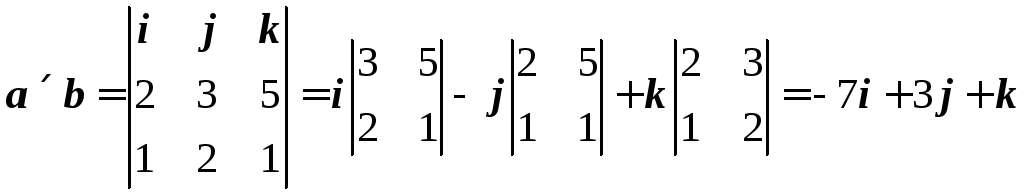5.
Вычислить площадь параллелограмма,
построенного на векторах:
и
.
Решение:
Находим векторное произведение
на
по формулам (5.6) и (5.7):
.
Так
как модуль векторного произведения
двух векторов равен площади построенного
на них параллелограмма, то
(кв. ед.).
6.
Вычислите площадь треугольника с
вершинами
и
.
Решение:
Площадь треугольника ABC
равна половине площади параллелограмма,
построенного на векторах
и
.
Найдем
координаты
этих векторов 
,
.
Далее находим векторное произведение
этих векторов по формулам (5.6) и (5.7):
.
Тогда
(кв.ед.).
7.
Вычислите площадь параллелограмма,
построенного на векторах
и
,
если
,
.
Решение: Используя свойства векторного произведения, имеем
(поскольку
,
).
Итак,
(кв.ед.).
8.
Показать, что векторы
,
,
компланарны.
Решение: Воспользуемся условием компаланарности векторов (5.9). Находим смешанное произведение векторов:
.
Так как , то заданные векторы компланарны.
9.
Доказать, что четыре точки
лежат
в одной плоскости.
Решение:
Достаточно показать, что три вектора
,
имеющие начало в одной из данных точек,
лежат в одной плоскости (т.е. компланарны).
Находим координаты векторов
,
,
.
Проверяем условие компланарности
векторов (5.9):
.
Итак,
векторы
компланарны, следовательно, точки
лежат в одной плоскости.
10.
Найти объем треугольной пирамиды с
вершинами
.
Решение:
Найдем векторы
,
совпадающие с ребрами пирамиды,
сходящимися в вершине A:
.
Смешанное произведение этих векторов равно по модулю объему параллелепипеда, построенного на них. Находим смешанное произведение этих векторов:
.
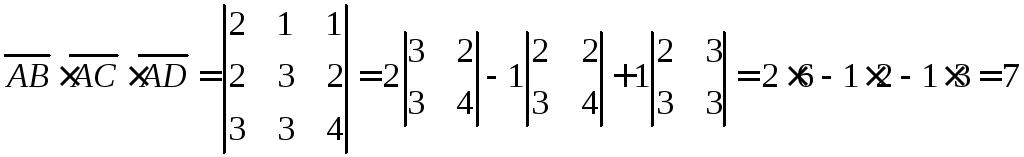Так
как объем пирамиды равен
объема параллелепипеда, построенного
на векторах
,
то
(куб.ед.).
11.
Даны вершины пирамиды
.
Найти
длину высоты, опущенной из вершины S
на грань ABC.
Решение:
Так как объем пирамиды есть
,
то
,
где
– высота пирамиды,
– площадь основания пирамиды. Находим
,
.
Находим :
.
Следовательно,
.
Задачи для самостоятельного решения
1.
Даны векторы
и
.
При каком значении
эти
векторы перпендикулярны?
2.
Определите угол между векторами
и
.
3.
Найти
,
если
,
.
4.
Даны векторы:
,
,
.
Найти
.
5.
Показать, что четырехугольник с вершинами
есть квадрат.
6.
Найти векторное произведение векторов
и
.
7.
Найти площадь параллелограмма,
построенного на векторах
и
.
8.
Найдите площадь треугольника с вершинами
.
9.
Векторы
составляют угол
.
Найти площадь параллелограмма,
построенного на векторах
и
,
где
.
10.
Дано:
,
,
.
Найти
.
11.
Показать, что точки
лежат
в одной плоскости.
12.
Найти объем параллелепипеда, построенного
на векторах
,
и
.
13.
Найти высоту параллелепипеда, построенного
на векторах
,
и
.
Высота опущена на грань, образованную
векторами
.
14.
Даны векторы
,
и
.
Найти:
.
15.
При каком значении
векторы
и
перпендикулярны?
16.
Определите угол между векторами
и
.
17.
Даны векторы
,
и
.
Найти
.
18.
Даны три последовательные вершины
параллелограмма:
.
Найти
его
четвертую вершину и угол между векторами
.
19.
Найти координаты вектора
,
если
;
.
20.
Найти площадь параллелограмма,
построенного на векторах
и
.
21.
Найти площадь треугольника с вершинами
,
и
.
22.
Векторы
составляют угол 45o.
Найти площадь треугольника, построенного
на векторах
и
,
если
.
23.
Показать, что векторы
,
и
компланарны.
24.
Найти объем параллелепипеда, построенного
на векторах
,
и
.
25.
Даны вершины пирамиды
.
Найти
длину высоты, опущенной на грань BCD.
Ответы:
1)
m
= 4;
2)
;3)
13; 4)
5; 6)
;
7)
;
8) 
;9)
;10)
;12)
12; 13)
;14)
(3;3;0); 15)
m
= 1;
16) 135о
17)
−4;
18)
;19)
;20)
60; 21)
;22) 
;24)
;25)
11.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 6