2. Деление отрезка в данном отношении.

Рассмотрим в пространстве две точки и . Пусть  – прямая, проходящая через точки и , а М – некоторая точка на этой прямой (см. рис. 4.1).

Говорят, что точка М делит отрезок в отношении, если выполняется равенство: .

Отметим, что  может быть любым числом, за исключением 1. Причем, если М лежит между точками и , то  – положительное, если М лежит правее точки или левее точки , то  – отрицательное.

Рис. 4.1

Координаты точки М могут быть найдены по формулам:

(4.7)

Эти формулы называются формулами деления отрезка в данном отношении.

В частности, если  = 1, то точка М делит отрезок пополам:

(4.8)

Заметим, что формулы (4.7) деления отрезка в данном отношении имеют смысл, только если   1.

Примеры решения задач

1. Даны две точки и. Найти координаты вектора.

Решение: Координаты находятся по формуле (4.1а):

.

В данном случае имеем: и, т.е..

2. При каких значениях векторыиколлинеарны?

Решение: Воспользуемся условием коллинеарности векторов (4.6). Так как , то . Отсюда находим, что.

3. Разложить вектор по векторами.

Решение: Требуется представить вектор в виде , где– некоторые числа. Найдем их, используя определение равенства векторов. Имеем,,и равенство, т.е.. Отсюда следует:

т.е. . Следовательно,.

4. Найти длину вектора и его направляющие косинусы.

Решение: Воспользуемся формулами (4.2а) и (4.4). Имеем

;

.

5. Нормировать вектор .

Решение: Найдем длину вектора по формуле(4.2а):

.

Искомый единичный вектор имеет вид:

.

6. Отрезок АВ разделен на пять равных частей. Известна первая точка деления С(3, –5, 7) и последняя F(–2, 4, –8). Определить координаты концов отрезка и его длину.

Решение: Точка С делит отрезок АВ в отношении , а точкаF делит отрезок АВ в отношении (см. рис. 4.2).

Рис. 4.2

Обозначим координаты точек А и В: ,. Воспользуемся формулами (4.7) деления отрезка в отношениии. Получим равенства:

Из этих равенств составим три системы:

Решая их, находим точки и.

Найдем теперь расстояние между точками А и В по формуле (4.2а):

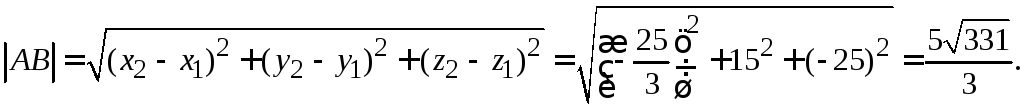
Задачи для самостоятельного решения

1. Найти вектор , если и.

2. Нормировать вектор .

3. Найти длину вектора и его направляющие косинусы.

4. Может ли вектор составлять с координатными осями следующие углы: .

5. Вектор составляет с осямииуглы. Какой угол он составляет с осью?

6. Даны векторы . При каком значении коэффициентавекторы и коллинеарны?

7. Представить вектор как линейную комбинацию векторов.

8. Найти длину медианы треугольника , если.

9. Найти вектор , если и.

10. Нормировать вектор .

11. Найти длину вектора и его направляющие косинусы.

12. Может ли вектор составлять с координатными осями следующие углы: .

13. Вектор составляет с осямииуглы. Вычислить его координаты при условии, что.

14. Даны точки . Проверить, коллинеарны ливекторы и .

15. Заданы векторы . Найти разложение векторапо базису.

16. Найти длину медианы AK треугольника ABC, если .

Ответы:

1) ;2) ;3) ;;4) не может; 5) или;6) ;7) ; 8) ;9) ;10) ;11) ;;12) может; 13) или;15) ;16) .

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 5