
- •Вычисление определителей 2-го, 3-го и высших порядков
- •1. Определитель 2-го и 3-го порядков.
- •2. Определитель произвольного порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Действия над матрицами, вычисление обратной матрицы. Решение матричных уравнений
- •1. Алгебра матриц.
- •2. Обратная матрица.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Решение систем линейных уравнений методом Крамера и Гаусса
- •1. Метод Крамера.
- •2. Метод Гаусса.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Векторная алгебра. Вычисление координат, модуля и направляющих косинусов вектора
- •1. Векторная алгебра.
- •2. Деление отрезка в данном отношении.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Скалярное, векторное и смешанное произведения векторов
- •1. Скалярное произведение векторов.
- •2. Векторное произведение векторов.
- •3. Смешанное произведение векторов.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Прямая линия на плоскости
- •1. Общее уравнение прямой.
- •2. Уравнение прямой в отрезках.
- •3. Каноническое уравнение прямой.
- •6. Параметрические уравнения прямой.
- •7. Прямая с угловым коэффициентом.
- •8. Нормальное уравнение прямой.
- •10. Условия параллельности и перпендикулярности прямых. Нахождение угла между прямыми.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Плоскость и прямая в пространстве
- •1. Общее уравнение плоскости.
- •2. Уравнение плоскости в отрезках.
- •3. Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой.
- •5. Уравнение плоскости, параллельной двум неколлинеарным векторам и проходящей через точку.
- •7. Нормальное уравнение плоскости.
- •9. Общие уравнения прямой.
- •10. Канонические уравнения прямой.
- •12. Параметрические уравнения прямой.
- •13. Взаимное расположение прямых и плоскостей.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Кривые второго порядка
- •1. Эллипс.
- •2. Гипербола.
- •3. Парабола.
- •4. Единое определение кривой второго порядка.
- •5. Полярное уравнение кривой второго порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Предел числовой последовательности. Предел функции
- •1. Предел числовой последовательности.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Раскрытие неопределенностей. Замечательные пределы
- •1. Замечательные пределы.
- •2. Сравнение бесконечно малых.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Непрерывность функции. Точки разрыва функции
- •1. Непрерывность функции.
- •2. Точки разрыва.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вычисление производных
- •1. Производная и ее геометрический и механический смысл.
- •3. Производные основных элементарных функций.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Производная неявной, параметрически заданной и сложно-степенной функции
- •Задачи для самостоятельного решения
- •Производные высших порядков. Дифференциал функции. Приложения дифференциалов
- •1. Производные высших порядков.
- •2. Дифференциал функции.
- •3. Формула приближенного вычисления.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Правило Лопиталя. Точки экстремума функции.
- •1. Правило Лопиталя.
- •2. Возрастание и убывание функции.
- •3. Точки экстремума функции.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Исследование функций и построение графиков
- •1. Выпуклость и вогнутость функции.
- •2. Точки перегиба функции.
- •3. Асимптоты функции.
- •4. Общий план исследования функции и построение графика.
- •Примеры решения задач
- •Задачи для самостоятельного решения
2. Метод Гаусса.
Матрица
 ,
получающаяся изА
приписыванием столбца свободных членов,
называется расширенной
матрицей.
,
получающаяся изА
приписыванием столбца свободных членов,
называется расширенной
матрицей.
Основная
идея метода Гаусса заключается в том,
что расширенная матрица
![]() системы уравнений (3.1) путем элементарных
преобразований над строками приводится
кступенчатой
форме,
когда все элементы ниже главной диагонали
обращены в нуль.
системы уравнений (3.1) путем элементарных
преобразований над строками приводится
кступенчатой
форме,
когда все элементы ниже главной диагонали
обращены в нуль.
 (3.3)
(3.3)
По полученной матрице выписывается система, которая, очевидно, будет эквивалентна исходной.
Если
в матрице (3.3) получилась строка с
единственным ненулевым элементом –
![]() ,
то
система несовместна, так как этой строке
соответствует уравнение
,
то
система несовместна, так как этой строке
соответствует уравнение
![]() ,
не имеющее решений. В противном случае
возможны два варианта:
,
не имеющее решений. В противном случае
возможны два варианта:
1)
r
= n
и
нижняя ненулевая строка матрицы (3.3)
определяет уравнение:
![]() .
Так как
.
Так как![]() ,
то имеем решение
,
то имеем решение![]() .
Подставим его в вышестоящее уравнение
и получим уравнение с одной неизвестной
.
Подставим его в вышестоящее уравнение
и получим уравнение с одной неизвестной![]() ,
решим
его и перейдем к следующему уравнению
и т.д. В результате получим единственное
решение системы: (х1,
х2
,
х3
,
. . . ,
хn
).
,
решим
его и перейдем к следующему уравнению
и т.д. В результате получим единственное
решение системы: (х1,
х2
,
х3
,
. . . ,
хn
).
2)
r
< n
и
нижняя ненулевая строка дает уравнение
с несколькими неизвестными:
![]() .
Назовем
.
Назовем![]() параметрами и выразим через них сначала
параметрами и выразим через них сначала![]() ,
а затем остальные переменные
,
а затем остальные переменные![]() .
Получаем бесконечное множество решений
системы.
.
Получаем бесконечное множество решений
системы.
Примеры решения задач
1.
Решить систему линейных уравнений
методом Крамера:

Решение. Вычислим определитель матрицы системы:
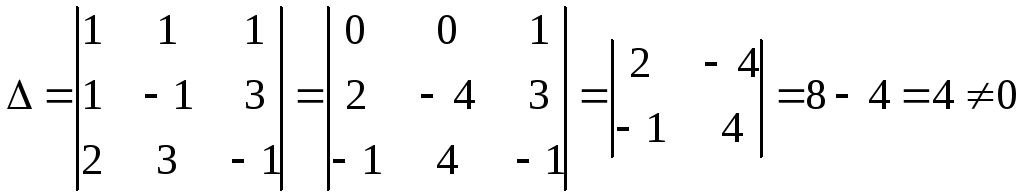 .
.
Так
как
![]() ,
то система имеет единственное решение,
которое находится по формулам Крамера.
Вычисляем
,
то система имеет единственное решение,
которое находится по формулам Крамера.
Вычисляем

![]() ,
,

 ,
,
 .
.
По формулам (3.2) находим решение системы:
![]() .
.
2.
Решить систему методом Гаусса:
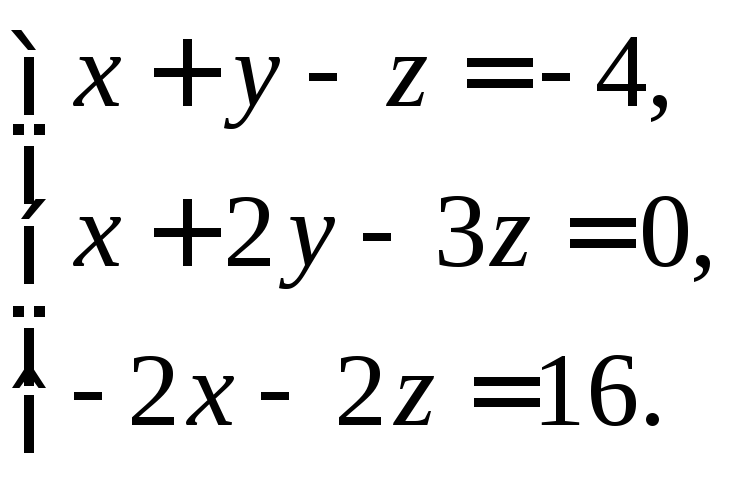
Решение: Составим расширенную матрицу системы и приведем ее к ступенчатому виду (3.3):
 ~
~ ~
~ .
.
Получили
ступенчатую матрицу. Выпишем по полученной
матрице систему, которая будет эквивалентна
исходной:
 Эта система совместна и имеет бесконечно
много решений. Из второго уравнения
находим:
Эта система совместна и имеет бесконечно
много решений. Из второго уравнения
находим:
![]() .
Из первого уравнения находим
.
Из первого уравнения находим![]() .
Таким образом, решение системы будут
составлять два равенства:
.
Таким образом, решение системы будут
составлять два равенства:![]() .
.
Задачи для самостоятельного решения
Решить системы методом Крамера:
1.
 2.
2. 3.
3.
4.
 5.
5.
6.
Решить систему методом Гаусса:

7.
Исследовать систему линейных уравнений.
Если система совместна, то найти общее
и одно ее частное решение:

Решить системы методом Крамера:
8.
 9.
9. 10.
10.
11.
 12.
12.
13.
Решить систему методом Гаусса: 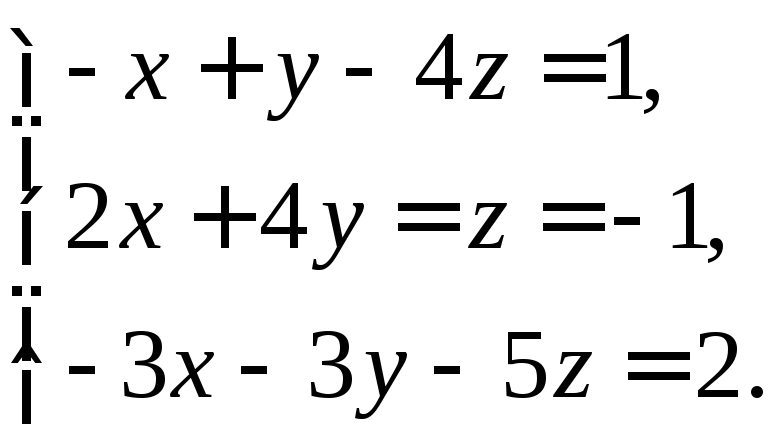
14.
Исследовать систему линейных уравнений.
Если система совместна, то найти общее
и одно ее частное решение:

Ответы:
1)
![]() ;
2)
;
2)
![]() ;3)
;3)
![]() ;
4)
;
4) ![]() ;5)
;5)
![]() ;6)
;6)
![]() ;7)
система несовместна; 8)
;7)
система несовместна; 8)
![]() ;9)
;9)
![]() ;10)
;10) ![]() ;11)
;11) ![]() ;12)
;12)
![]() ;13)
;13) ![]() ;14) система
совместна и определенна, о.р. = ч.р.:
(2; 3; 5).
;14) система
совместна и определенна, о.р. = ч.р.:
(2; 3; 5).
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 4
Векторная алгебра. Вычисление координат, модуля и направляющих косинусов вектора
1. Векторная алгебра.
Вектором на плоскости и в пространстве называется направленный отрезок.
Помимо
обозначения
![]() ,
гдеА
начало вектора, а В
– его конец, будем использовать также
малые латинские буквы, выделенные жирным
шрифтом: а,
b,
c,
… .
,
гдеА
начало вектора, а В
– его конец, будем использовать также
малые латинские буквы, выделенные жирным
шрифтом: а,
b,
c,
… .
Длиной
вектора называется расстояние между
началом и концом вектора. Длину вектора
называют еще модулем
вектора и обозначают
![]() .
.
Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Назовем два вектора равными, если они коллинеарны, имеют одинаковые длины и одинаковые направления.
Если
известны координаты точек
![]() и
и![]() ,
то координаты вектораа
=
,
то координаты вектораа
=
![]() вычисляются по
формулам:
вычисляются по
формулам:
![]() (4.1а)
(4.1а)
Формулы
для вычисления длины
вектора а![]() ,
а также
расстояния
между точками
,
а также
расстояния
между точками
![]() и
и
![]() :
:
![]()
![]() (4.2а)
(4.2а)
Декартовы
координаты на плоскости определяются
аналогично, с той разницей, что там
отсутствует ось аппликат и, соответственно,
третья координата. Таким образом, если
а =![]() и
и![]() ,
то, очевидно,
,
то, очевидно,
![]() (4.1б)
(4.1б)
![]()
![]() (4.2б)
(4.2б)
Обозначим , и – углы наклона вектора а к координатным осям Ох, Оу и Оz, соответственно. Три числа cos, cos и cos называются направляющими косинусами вектора а.
Справедливы равенства:
![]() (4.3)
(4.3)
Формулы для вычисления направляющих косинусов:
 (4.4)
(4.4)
Если равенства (4.4) возвести в квадрат и сложить, то получим:
![]() (4.5)
(4.5)
Приведем еще условие коллинеарности двух векторов:
![]() (4.6)
(4.6)
Таким образом, два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны.
