
- •Вычисление определителей 2-го, 3-го и высших порядков
- •1. Определитель 2-го и 3-го порядков.
- •2. Определитель произвольного порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Действия над матрицами, вычисление обратной матрицы. Решение матричных уравнений
- •1. Алгебра матриц.
- •2. Обратная матрица.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Решение систем линейных уравнений методом Крамера и Гаусса
- •1. Метод Крамера.
- •2. Метод Гаусса.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Векторная алгебра. Вычисление координат, модуля и направляющих косинусов вектора
- •1. Векторная алгебра.
- •2. Деление отрезка в данном отношении.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Скалярное, векторное и смешанное произведения векторов
- •1. Скалярное произведение векторов.
- •2. Векторное произведение векторов.
- •3. Смешанное произведение векторов.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Прямая линия на плоскости
- •1. Общее уравнение прямой.
- •2. Уравнение прямой в отрезках.
- •3. Каноническое уравнение прямой.
- •6. Параметрические уравнения прямой.
- •7. Прямая с угловым коэффициентом.
- •8. Нормальное уравнение прямой.
- •10. Условия параллельности и перпендикулярности прямых. Нахождение угла между прямыми.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Плоскость и прямая в пространстве
- •1. Общее уравнение плоскости.
- •2. Уравнение плоскости в отрезках.
- •3. Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой.
- •5. Уравнение плоскости, параллельной двум неколлинеарным векторам и проходящей через точку.
- •7. Нормальное уравнение плоскости.
- •9. Общие уравнения прямой.
- •10. Канонические уравнения прямой.
- •12. Параметрические уравнения прямой.
- •13. Взаимное расположение прямых и плоскостей.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Кривые второго порядка
- •1. Эллипс.
- •2. Гипербола.
- •3. Парабола.
- •4. Единое определение кривой второго порядка.
- •5. Полярное уравнение кривой второго порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Предел числовой последовательности. Предел функции
- •1. Предел числовой последовательности.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Раскрытие неопределенностей. Замечательные пределы
- •1. Замечательные пределы.
- •2. Сравнение бесконечно малых.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Непрерывность функции. Точки разрыва функции
- •1. Непрерывность функции.
- •2. Точки разрыва.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вычисление производных
- •1. Производная и ее геометрический и механический смысл.
- •3. Производные основных элементарных функций.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Производная неявной, параметрически заданной и сложно-степенной функции
- •Задачи для самостоятельного решения
- •Производные высших порядков. Дифференциал функции. Приложения дифференциалов
- •1. Производные высших порядков.
- •2. Дифференциал функции.
- •3. Формула приближенного вычисления.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Правило Лопиталя. Точки экстремума функции.
- •1. Правило Лопиталя.
- •2. Возрастание и убывание функции.
- •3. Точки экстремума функции.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Исследование функций и построение графиков
- •1. Выпуклость и вогнутость функции.
- •2. Точки перегиба функции.
- •3. Асимптоты функции.
- •4. Общий план исследования функции и построение графика.
- •Примеры решения задач
- •Задачи для самостоятельного решения
Задачи для самостоятельного решения
1. Найти производную функции указанного порядка:
а)
y
= x
cos x![]() ,
y′′′
– ? б)
y
=
,
y′′′
– ? б)
y
=
![]() ,
y
,
y![]() –?
–?
в)
y
= sin![]() x,
y
x,
y![]() – ?
– ?
2. Найти дифференциал функции указанного порядка:
а)
u
=
![]() ,d
,d![]() u
– ? б) y
= (4х
+ 3)·2
u
– ? б) y
= (4х
+ 3)·2![]() ,d
,d![]() y
– ?
y
– ?
3. Найти производную функции указанного порядка:
а)
у
=
![]() ,y′′′
– ? б) y
=
,y′′′
– ? б) y
=
 ,
y′′
– ?
,
y′′
– ?
в)
 y′′
y′′![]() – ? г) у
= 3
– ? г) у
= 3![]() ,y
,y![]() – ?
– ?
4. Насколько приблизительно увеличится объём шара, если его радиус R = 15 см удлинится на 2 мм?
5. Вычислить приближенно:
а)
![]() ;
б)lg
0,9; в) sin
31°.
;
б)lg
0,9; в) sin
31°.
6.
Удовлетворяет ли функция у
=
![]() уравнениюу
уравнениюу![]() у′′
+ 1 = 0?
у′′
+ 1 = 0?
7. Найти дифференциал функции указанного порядка:
а)
z
=
![]() + arcsin
+ arcsin![]() x,
dz
– ? б)
y
= 4
x,
dz
– ? б)
y
= 4![]() ,
d
,
d![]() y
– ?
y
– ?
в)
u
=
 ,
d
,
d![]() u
– ? г) ln
u
– ? г) ln![]() = arctg
= arctg![]() ,
dy
– ?
,
dy
– ?
Ответы:
1) а) ![]() ;
б)
;
б) ;
в)
;
в)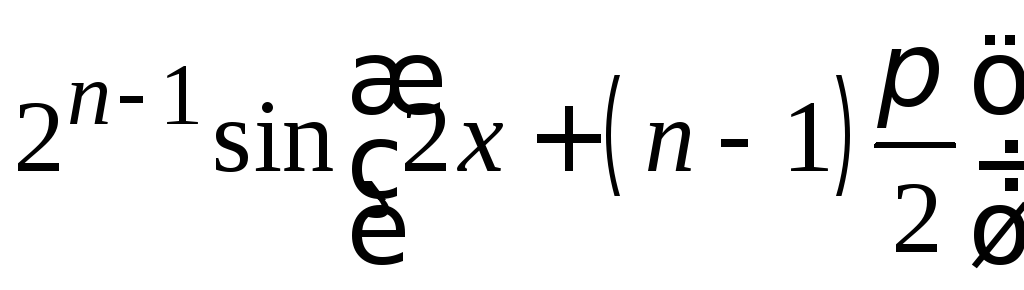 ;2) а)
;2) а) 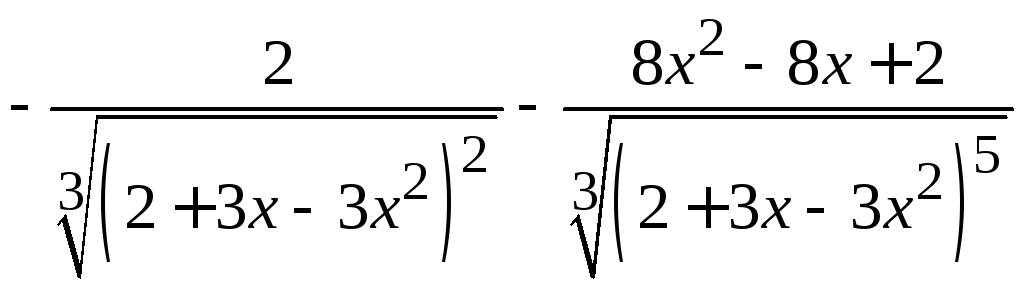 ;
б)
;
б)![]() ;3) а)
;3) а) ![]() ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)![]() ;4) 565
;4) 565![]() ;5) а) 2,03;
б) –0,045; в) 0,515; 6)
да; 7) а)
;5) а) 2,03;
б) –0,045; в) 0,515; 6)
да; 7) а)  ;
б)
;
б)![]() ;
в)
;
в)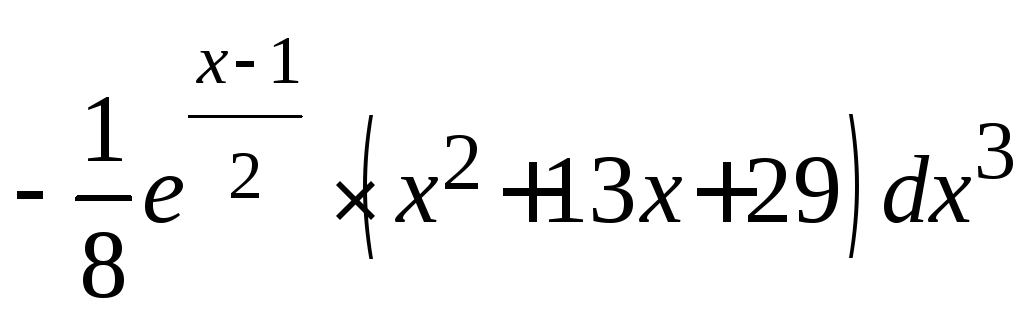 ;
г)
;
г) .
.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 15
Правило Лопиталя. Точки экстремума функции.
1. Правило Лопиталя.
Пусть
функции
![]() непрерывны и дифференцируемы в некоторой
окрестности точки a,
за исключением может быть самой
точки
a
(а
–
число или
непрерывны и дифференцируемы в некоторой
окрестности точки a,
за исключением может быть самой
точки
a
(а
–
число или
![]() ).
Причем
).
Причем![]() в любой точке этой окрестности и выполнено
одно из условий:
в любой точке этой окрестности и выполнено
одно из условий:

Тогда
если существует
 ,
то существует и
,
то существует и ,
причем
,
причем
 (15.1)
(15.1)
(![]() – число или
– число или![]() ).
).
Правило
Лопиталя позволяет раскрывать
неопределенности вида
![]() или
или![]() .
Правило Лопиталя можно применять
несколько раз подряд, но только конечное
число раз, пока не исчезнет неопределенность.
Остальные виды неопределенностей
приводятся к ним следующим образом:
.
Правило Лопиталя можно применять
несколько раз подряд, но только конечное
число раз, пока не исчезнет неопределенность.
Остальные виды неопределенностей
приводятся к ним следующим образом:
1)
().
Преобразование
 дает неопределенность вида
дает неопределенность вида![]() .
.
2)
().
Преобразование
 дает неопределенность вида
дает неопределенность вида![]() ,
еслиf(x)
– бесконечно малая функция, а g(x)
бесконечно большая, или неопределенность
вида
,
еслиf(x)
– бесконечно малая функция, а g(x)
бесконечно большая, или неопределенность
вида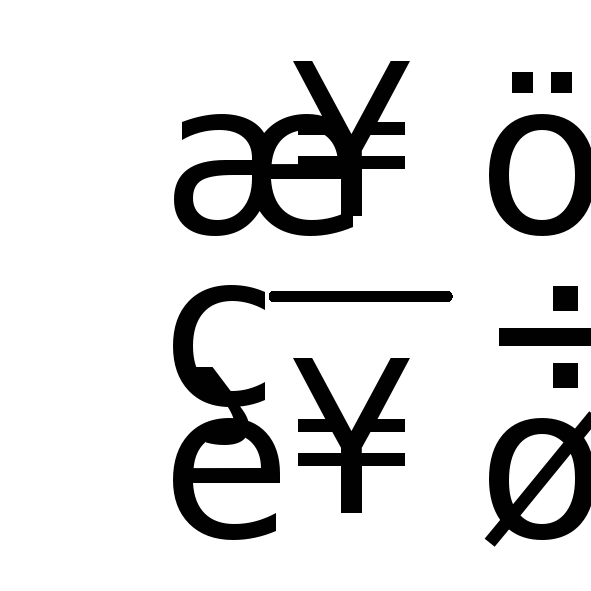 ,
в противном случае.
,
в противном случае.
3)
![]() Преобразуем функцию следующим образом
Преобразуем функцию следующим образом
![]() ,
тогда в степени получим неопределенность
вида ().
,
тогда в степени получим неопределенность
вида ().
2. Возрастание и убывание функции.
Если
производная дифференцируемой функции
строго положительна внутри некоторого
промежутка, т.е.
![]() ,
то функция строго монотонно возрастает
на этом промежутке.
,
то функция строго монотонно возрастает
на этом промежутке.
Если
производная дифференцируемой функции
строго отрицательна внутри некоторого
промежутка, т.е.
![]() ,
то функция строго монотонно убывает на
этом промежутке.
,
то функция строго монотонно убывает на
этом промежутке.
3. Точки экстремума функции.
Точка
![]() называетсяточкой
максимума (рис.
15.1) (минимума
(рис. 15.2)) функции
называетсяточкой
максимума (рис.
15.1) (минимума
(рис. 15.2)) функции
![]() ,
если существует окрестность
,
если существует окрестность![]() этой точки, такая, что
этой точки, такая, что![]() .
.


Рис. 15.1 Рис. 15.2
Точки максимума и минимума называются точками экстремума функции.
Необходимое
условие экстремума.
Пусть функция непрерывна в некоторой
окрестности точки
![]() и имеет экстремум в этой точке. Тогда
производная функции в точке
и имеет экстремум в этой точке. Тогда
производная функции в точке![]() либо равна нулю, либо не существует.
либо равна нулю, либо не существует.
Геометрически это означает, что в точке экстремума функции y=f(x) касательная к ее графику либо параллельна оси OX (как на рисунке 15.3), либо не существует (как на рисунке 15.4).


Рис. 15.3 Рис. 15.4
Достаточные
условия экстремума.
Пусть функция f(x)
определена в точке
![]() ,
непрерывна в некоторой окрестности
точки
,
непрерывна в некоторой окрестности
точки![]() и дифференцируема в этой окрестности,
за исключением может быть самой точки
и дифференцируема в этой окрестности,
за исключением может быть самой точки![]() .
Тогда если производная
.
Тогда если производная![]() меняет знак при переходе через точку
меняет знак при переходе через точку![]() ,
то
,
то![]() является точкой экстремума. При этом,
если при переходе через точку
является точкой экстремума. При этом,
если при переходе через точку![]() производная меняет знак с «+» на «–»,
то
производная меняет знак с «+» на «–»,
то![]() – точка максимума; если с «–» на «+»,
то
– точка максимума; если с «–» на «+»,
то![]() – точка минимума. Если знак производной
при переходе через точку
– точка минимума. Если знак производной
при переходе через точку![]() не меняется, то
не меняется, то![]() не является точкой экстремума.
не является точкой экстремума.
Точки,
в которых производная
![]() равна нулю или не существует, называютсякритическими
точками.
Из последней теоремы следует, что
критические точки необязательно будут
точками экстремума.
равна нулю или не существует, называютсякритическими
точками.
Из последней теоремы следует, что
критические точки необязательно будут
точками экстремума.
Общее
условие существования экстремума.
Пусть в точке
![]() функция
функция![]() имеет производные доп-го
порядка включительно, причем
имеет производные доп-го
порядка включительно, причем
![]() .
.
Тогда,
если п
– четное, то функция
![]() имеет в точке
имеет в точке![]() экстремум, а именно максимум, если
экстремум, а именно максимум, если![]() ,
и минимум, если
,
и минимум, если![]() .
Еслип
– нечетное, то функция
.
Еслип
– нечетное, то функция
![]() не имеет экстремум в точке
не имеет экстремум в точке![]() .
.
На практике часто применяется следствие из этого утверждения:
Если
для функции f(x)
в точке
![]() первая производная
первая производная
![]() равна нулю, а вторая производная
равна нулю, а вторая производная
![]() отлична от нуля, т.е.
отлична от нуля, т.е.
![]() ,
,
![]() ,
то
,
то
![]() является точкой экстремума функцииf(x),
причем
является точкой экстремума функцииf(x),
причем
1)
если
![]() ,
то
,
то
![]() – точка минимума функцииf(x);
– точка минимума функцииf(x);
2)
если
![]() ,
то
,
то
![]() – точка максимума функцииf(x).
– точка максимума функцииf(x).
