
- •Вычисление определителей 2-го, 3-го и высших порядков
- •1. Определитель 2-го и 3-го порядков.
- •2. Определитель произвольного порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Действия над матрицами, вычисление обратной матрицы. Решение матричных уравнений
- •1. Алгебра матриц.
- •2. Обратная матрица.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Решение систем линейных уравнений методом Крамера и Гаусса
- •1. Метод Крамера.
- •2. Метод Гаусса.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Векторная алгебра. Вычисление координат, модуля и направляющих косинусов вектора
- •1. Векторная алгебра.
- •2. Деление отрезка в данном отношении.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Скалярное, векторное и смешанное произведения векторов
- •1. Скалярное произведение векторов.
- •2. Векторное произведение векторов.
- •3. Смешанное произведение векторов.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Прямая линия на плоскости
- •1. Общее уравнение прямой.
- •2. Уравнение прямой в отрезках.
- •3. Каноническое уравнение прямой.
- •6. Параметрические уравнения прямой.
- •7. Прямая с угловым коэффициентом.
- •8. Нормальное уравнение прямой.
- •10. Условия параллельности и перпендикулярности прямых. Нахождение угла между прямыми.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Плоскость и прямая в пространстве
- •1. Общее уравнение плоскости.
- •2. Уравнение плоскости в отрезках.
- •3. Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой.
- •5. Уравнение плоскости, параллельной двум неколлинеарным векторам и проходящей через точку.
- •7. Нормальное уравнение плоскости.
- •9. Общие уравнения прямой.
- •10. Канонические уравнения прямой.
- •12. Параметрические уравнения прямой.
- •13. Взаимное расположение прямых и плоскостей.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Кривые второго порядка
- •1. Эллипс.
- •2. Гипербола.
- •3. Парабола.
- •4. Единое определение кривой второго порядка.
- •5. Полярное уравнение кривой второго порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Предел числовой последовательности. Предел функции
- •1. Предел числовой последовательности.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Раскрытие неопределенностей. Замечательные пределы
- •1. Замечательные пределы.
- •2. Сравнение бесконечно малых.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Непрерывность функции. Точки разрыва функции
- •1. Непрерывность функции.
- •2. Точки разрыва.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вычисление производных
- •1. Производная и ее геометрический и механический смысл.
- •3. Производные основных элементарных функций.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Производная неявной, параметрически заданной и сложно-степенной функции
- •Задачи для самостоятельного решения
- •Производные высших порядков. Дифференциал функции. Приложения дифференциалов
- •1. Производные высших порядков.
- •2. Дифференциал функции.
- •3. Формула приближенного вычисления.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Правило Лопиталя. Точки экстремума функции.
- •1. Правило Лопиталя.
- •2. Возрастание и убывание функции.
- •3. Точки экстремума функции.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Исследование функций и построение графиков
- •1. Выпуклость и вогнутость функции.
- •2. Точки перегиба функции.
- •3. Асимптоты функции.
- •4. Общий план исследования функции и построение графика.
- •Примеры решения задач
- •Задачи для самостоятельного решения
Производные высших порядков. Дифференциал функции. Приложения дифференциалов
1. Производные высших порядков.
Пусть
![]() дифференцируема в точке
дифференцируема в точке![]() .
Если
.
Если![]() также дифференцируема в точкеx
также дифференцируема в точкеx![]() ,
то значение выражения
,
то значение выражения
![]() называетсявторой
производной
функции
называетсявторой
производной
функции
![]() в точкеx
в точкеx![]() и обозначается
и обозначается
![]() или
или
По
индукции определяется производная
nго
порядка
в точке x![]() ,
как производная от производной (n
– 1)-го
порядка
и
обозначается
,
как производная от производной (n
– 1)-го
порядка
и
обозначается
![]() или
или
Пусть
дана сложная функция
![]() ,
где
,
где![]() ,
причем функции
,
причем функции![]() и
и![]() имеют производные 1-го и 2-го порядков.
Тогда сложная функция
имеют производные 1-го и 2-го порядков.
Тогда сложная функция![]() так же имеет вторую производную. Поскольку
так же имеет вторую производную. Поскольку![]() ,
то
,
то
![]() .
.
Следовательно,
![]() (14.1)
(14.1)
Аналогично вычисляются производные 3-го и высших порядков сложной функции.
Пусть
функция задана параметрически
 Если существуют вторые производные
Если существуют вторые производные![]() и
и![]() ,
то существует и
,
то существует и![]() .
Действительно, так как
.
Действительно, так как ,
то
,
то
 .
.
Отсюда получаем
 (14.2)
(14.2)
Аналогично можно находить производные 3-го и высших порядков от функции, заданной параметрически.
2. Дифференциал функции.
Из
определения производной
![]() следует равенство
следует равенство![]() ,
где
,
где![]() является бесконечно малой величиной.
является бесконечно малой величиной.
Величина
![]() называется
дифференциалом
функции
f
(x)
и обозначается dy.
называется
дифференциалом
функции
f
(x)
и обозначается dy.
Величина
![]() называетсядифференциалом
независимой переменной
и обозначается
называетсядифференциалом
независимой переменной
и обозначается
![]() .
Тогда дифференциал функции вычисляется
по формуле:
.
Тогда дифференциал функции вычисляется
по формуле:
![]() (14.3)
(14.3)
Пусть
![]() дважды дифференцируема в точкех.
Дифференциал от дифференциала этой
функции в точке х
называется дифференциалом
второго
порядка:
дважды дифференцируема в точкех.
Дифференциал от дифференциала этой
функции в точке х
называется дифференциалом
второго
порядка:
![]() (14.4)
(14.4)
Если
![]() n
раз
дифференцируема в точке x,
то по индукции можно определить
дифференциал
nго
порядка
функции
n
раз
дифференцируема в точке x,
то по индукции можно определить
дифференциал
nго
порядка
функции
![]() в точкеx:
в точкеx:
![]() (14.5)
(14.5)
Формулы (14.4) и (14.5) справедливы, только если х является независимой переменной.
Рассмотрим
сложную функцию:
![]() ,
где
,
где![]() .
Найдем дифференциал второго порядка
сложной функции. Так как
.
Найдем дифференциал второго порядка
сложной функции. Так как![]() ,
то имеем
,
то имеем
![]() ,
,
следовательно, получаем формулу второго дифференциала сложной функции:
![]() (14.6)
(14.6)
3. Формула приближенного вычисления.
Если
∆x
мало, то приращение
![]() отличается от дифференциала
отличается от дифференциала
![]() на
бесконечно малую величину более высокого
порядка, чем ∆x.
Отсюда имеем приближенное равенство
на
бесконечно малую величину более высокого
порядка, чем ∆x.
Отсюда имеем приближенное равенство
![]() или
или
![]() .
.
Тогда
![]() (14.7)
(14.7)
Это и есть формула приближенного вычисления.
Примеры решения задач
1. Найти производные 2-го порядка от следующих функций:
а)
у
= sin![]() x;
б) у
= ln
x;
б) у
= ln![]() .
.
Решение: а) Найдем сначала производную первого порядка:
у′
= (sin![]() x)′
= 2sin
x·cos
x
= sin
2x,
x)′
= 2sin
x·cos
x
= sin
2x,
а затем производную второго порядка:
y′′ = (sin 2x)′ = cos 2x·(2x)′ = 2cos 2x.
б) Находим производную первого порядка и затем второго:
у′
= (ln![]() )′
=
)′
=
 ·(
·(![]() )′
=
)′
=
 ·
·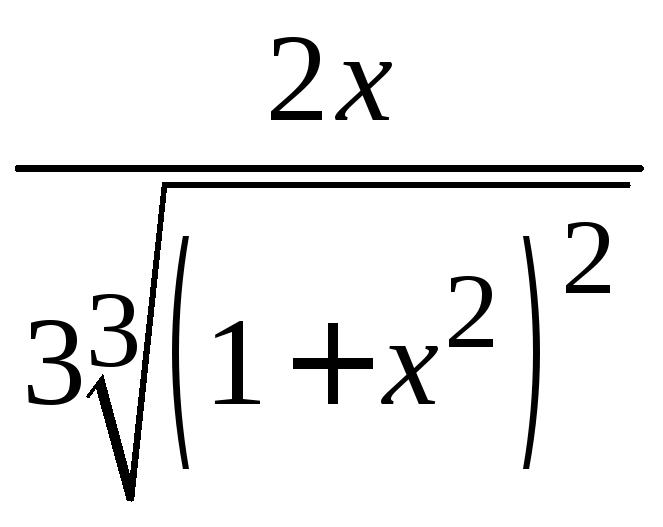 =
=
![]() ·
· ;
;
y′′
=
![]() ·
· =
=
![]() ·
· =
=
![]() ·
·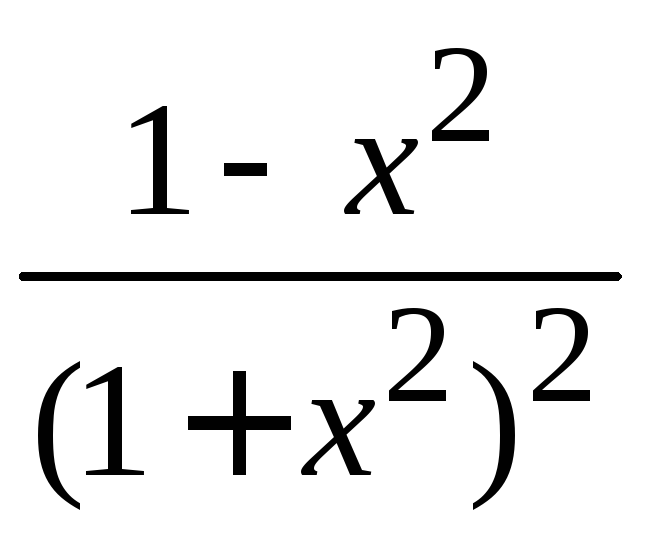 .
.
2.
Найти производную п-го
порядка от функции у
= log![]() (x
+ 5).
(x
+ 5).
Решение: Находим последовательно несколько производных данной функции:
у′
= (log![]() (x
+ 5))′ =
(x
+ 5))′ =
![]() ·(x
+ 5)′ =
·(x
+ 5)′ =
![]() ·
·![]() ,
,
у′′
=
 =
=![]() ·
· = –
= –![]() ·
· ,
,
у′′′
=
![]() ·
· =
=![]() ·
· =
=![]() ·
· ,
,
у![]() =
=
![]() ·
· =
=![]() ·
· =
= ,
,
Можно заметить закономерность и доказать формулу п-й производной методом математической индукции.
у![]() = (–1)
= (–1)![]()
 .
.
3.
Найти у′′
в точке (0; 1)
, если функция у
задана неявно уравнением
х![]() – ху
+ у
– ху
+ у![]() = 1.
= 1.
Решение: Дифференцируем данное уравнение по х и находим первую производную:
4х![]() – (х′у
+ ху′)
+ 4у
– (х′у
+ ху′)
+ 4у![]() ·у′
= 0,
·у′
= 0,
4х![]() – у
– ху′
+ 4у
– у
– ху′
+ 4у![]() ·у′
= 0,
·у′
= 0,
у′
=
 .
.
Теперь находим вторую производную:
у′′
=
 =
=
=
 .
.
Подставляя вместо у′ его значение, получим:
у′′
=
 =
=
=
 .
.
Значение
у′′
в точке (0; 1) равно
![]() .
.
4.
Найти у′′′![]() от функции
от функции
Решение:
у′![]() =
= =
=![]() ;
;
у′′![]() =
= =
= ;
;
у′′′![]() =
= =
= .
.
5.
Найти дифференциал dy,
если у
=
![]() arctg
arctg![]() +
+
![]() ln
ln![]() .
.
Решение: Используем формулу (14.3):
dy
=
![]() arctg
arctg![]() +
+![]() ln
ln![]() dx
=
dx
=
=
![]() ·
· ·
· +
+
![]() ·
·![]() ·
·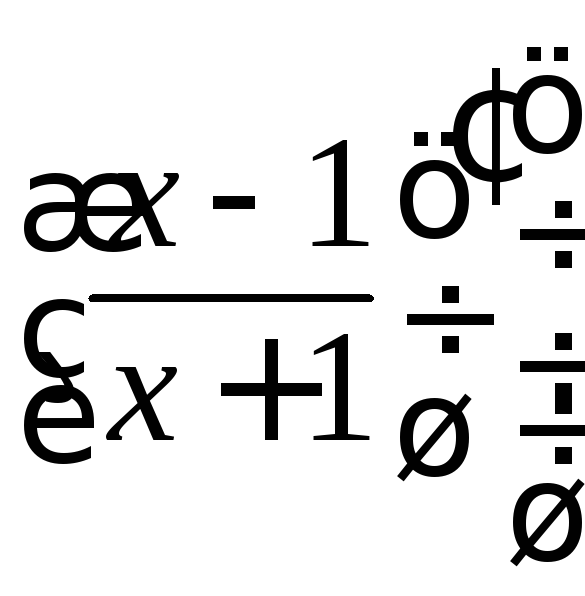 dx
=
dx
=
=
![]() ·
· ·
·![]() +
+
![]() ·
·![]() ·
· dx
=
dx
=
 dx.
dx.
6.
Насколько приблизительно изменится
сторона квадрата, если площадь его
увеличилась от 9 м![]() до 9,1 м
до 9,1 м![]() ?
?
Решение: Пусть у – сторона квадрата, х – площадь квадрата, тогда
![]() .
.
По условию задачи: х = 9, Δх = 0,1. Приращение стороны квадрата вычисляем приближенно по формуле, которая получается из (14.7):
f(x + Δx) – f(x) ≈ f′(x)·Δx
f(9,1)
– f(9)
=
![]() ≈f′(9)·0,1
≈f′(9)·0,1
f′(x)
=
![]() ,
f′(9)
=
,
f′(9)
=
![]() ,
тогда Δу
≈
,
тогда Δу
≈
![]() ·0,1
= 0,016м.
·0,1
= 0,016м.
7. Найти приближенное значение arctg 1,05.
Решение:
Воспользуемся формулой (14.7). Обозначим
х = 1,
тогда Δх =0,05.
Так как f(x)
= arctg
х,
то f(1)
= arctg
1 =
![]() ,
f′(x)
=
,
f′(x)
=
 ,f′(1)
=
,f′(1)
=
![]() .
Подставляем все данные в формулу (14.7):
.
Подставляем все данные в формулу (14.7):
arctg
1,05 ≈
![]() +
+
![]() ·0,05
= 0,81.
·0,05
= 0,81.
8.
Найти d![]() y,
если у
=
y,
если у
=
![]() +
+![]() .
.
Решение:
dy
= y′dx
=
 dx
=
dx
=
 dx,
dx,
d![]() y
=
y′′dx
y
=
y′′dx![]() =
=
 dx
dx![]() =
=
=
 dx
dx![]() =
=
=
 dx
dx![]() =
=
 dx
dx![]() ,
,
d![]() y
= y′′′dx
y
= y′′′dx![]() =
=
 dx
dx![]() =
=
=
 dx
dx![]() =
=
=
 dx
dx![]() =
=
=
 dx
dx![]() .
.
