
- •Вычисление определителей 2-го, 3-го и высших порядков
- •1. Определитель 2-го и 3-го порядков.
- •2. Определитель произвольного порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Действия над матрицами, вычисление обратной матрицы. Решение матричных уравнений
- •1. Алгебра матриц.
- •2. Обратная матрица.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Решение систем линейных уравнений методом Крамера и Гаусса
- •1. Метод Крамера.
- •2. Метод Гаусса.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Векторная алгебра. Вычисление координат, модуля и направляющих косинусов вектора
- •1. Векторная алгебра.
- •2. Деление отрезка в данном отношении.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Скалярное, векторное и смешанное произведения векторов
- •1. Скалярное произведение векторов.
- •2. Векторное произведение векторов.
- •3. Смешанное произведение векторов.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Прямая линия на плоскости
- •1. Общее уравнение прямой.
- •2. Уравнение прямой в отрезках.
- •3. Каноническое уравнение прямой.
- •6. Параметрические уравнения прямой.
- •7. Прямая с угловым коэффициентом.
- •8. Нормальное уравнение прямой.
- •10. Условия параллельности и перпендикулярности прямых. Нахождение угла между прямыми.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Плоскость и прямая в пространстве
- •1. Общее уравнение плоскости.
- •2. Уравнение плоскости в отрезках.
- •3. Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой.
- •5. Уравнение плоскости, параллельной двум неколлинеарным векторам и проходящей через точку.
- •7. Нормальное уравнение плоскости.
- •9. Общие уравнения прямой.
- •10. Канонические уравнения прямой.
- •12. Параметрические уравнения прямой.
- •13. Взаимное расположение прямых и плоскостей.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Кривые второго порядка
- •1. Эллипс.
- •2. Гипербола.
- •3. Парабола.
- •4. Единое определение кривой второго порядка.
- •5. Полярное уравнение кривой второго порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Предел числовой последовательности. Предел функции
- •1. Предел числовой последовательности.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Раскрытие неопределенностей. Замечательные пределы
- •1. Замечательные пределы.
- •2. Сравнение бесконечно малых.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Непрерывность функции. Точки разрыва функции
- •1. Непрерывность функции.
- •2. Точки разрыва.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вычисление производных
- •1. Производная и ее геометрический и механический смысл.
- •3. Производные основных элементарных функций.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Производная неявной, параметрически заданной и сложно-степенной функции
- •Задачи для самостоятельного решения
- •Производные высших порядков. Дифференциал функции. Приложения дифференциалов
- •1. Производные высших порядков.
- •2. Дифференциал функции.
- •3. Формула приближенного вычисления.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Правило Лопиталя. Точки экстремума функции.
- •1. Правило Лопиталя.
- •2. Возрастание и убывание функции.
- •3. Точки экстремума функции.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Исследование функций и построение графиков
- •1. Выпуклость и вогнутость функции.
- •2. Точки перегиба функции.
- •3. Асимптоты функции.
- •4. Общий план исследования функции и построение графика.
- •Примеры решения задач
- •Задачи для самостоятельного решения
3. Производные основных элементарных функций.
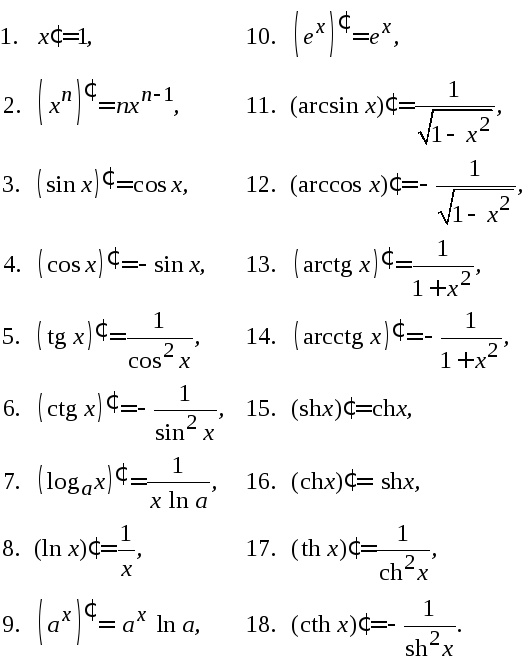 (12.7)
(12.7)
Примеры решения задач
1.
Исходя из определения производной,
вычислить у′(8),
если у
=
![]() .
.
Решение: По определению производной (12.1) имеем
у′
=

у′(8)
=
 =
=
![]() =
=
 =
= =
=
![]() .
.
2. Найти производные следующих функций, используя правила дифференцирования и таблицу производных:
а)
у
=
![]() –
–![]() +
+![]() ;
б)у
= е
;
б)у
= е![]() cos
x
+
cos
x
+
![]() .
.
Решение: а) используем правило дифференцирования суммы и производную константы, а также формулу 2 из таблицы производных (12.7):
у′
= (![]() –
–![]() +
+![]() )′
= (
)′
= (![]() )′
– (
)′
– (![]() )′
+ (
)′
+ (![]() )′
=
)′
=
=
5(х![]() )′
– (
)′
– (![]() )′
+ (
)′
+ (![]() )′
= 5·
)′
= 5·![]() х
х![]() + 3
+ 3![]() + 0 = –
+ 0 = –![]() +
+![]() ;
;
б) используем правила дифференцирования произведения (12.4) и частного (12.5), а также формулы 2, 4, 8 и 10 из таблицы производных (12.7):
у′
= (е![]() cos
x)′
+
cos
x)′
+
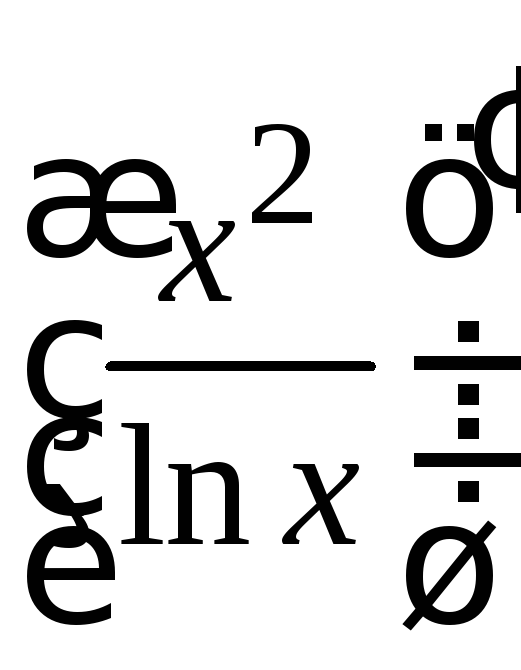 = (е
= (е![]() )′cos
x
+ е
)′cos
x
+ е![]() (cos
x)′
+
(cos
x)′
+
 =
=
=
е![]() cos
x
– е
cos
x
– е![]() sin
x
+
sin
x
+
 = е
= е![]() (cos
x
– sin x)
+
(cos
x
– sin x)
+
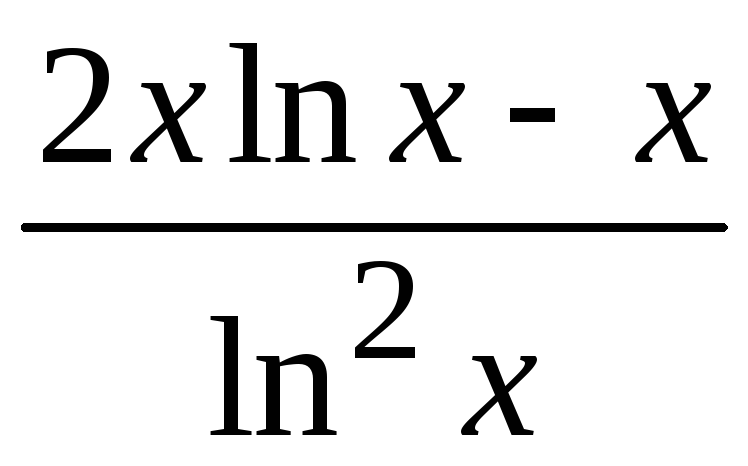 .
.
3. Найти производные следующих функций, используя правило дифференцирования сложной функции:
а)
у
= arccos![]() x;
б) y
=
x;
б) y
=
![]() ;
в) y
= tg
;
в) y
= tg![]() ln
ln![]() .
.
Решение: а) используем правило дифференцирования сложной функции (12.6), а также формулу 12 из таблицы производных (12.7):
у′
= (arccos![]() x)′
= 2arccos x
· (arccos x)′
= 2arccos x
·
x)′
= 2arccos x
· (arccos x)′
= 2arccos x
· = –
= – ;
;
б) снова воспользуемся производной сложной функции (12.6):
y′
=
 =
=
 =
=
![]()
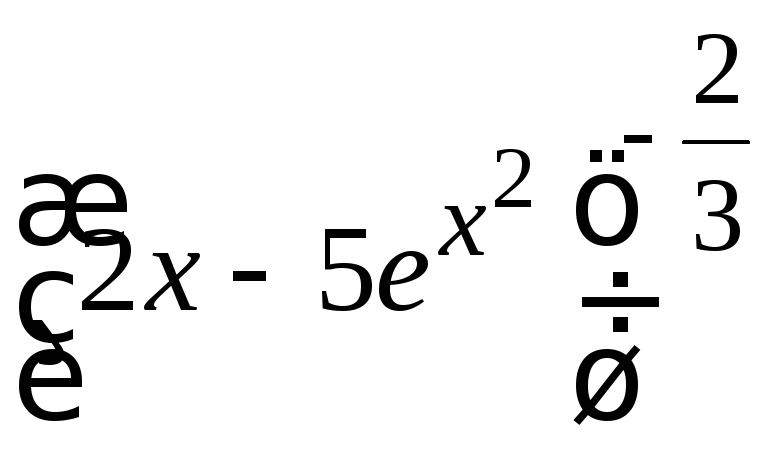 ·
· =
=
=
![]()

 =
=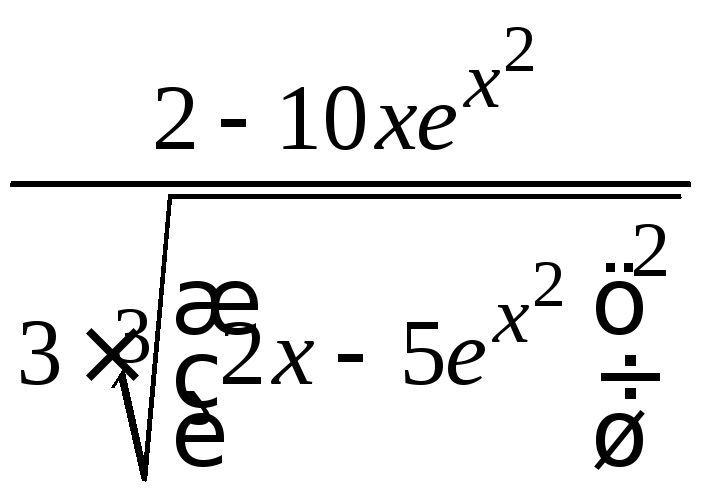 ;
;
в) в этом примере необходимо использовать правило дифференцирования сложной функции (12.6) трижды, а в конце надо использовать правило дифференцирования дроби (12.5):
y′
= (tg![]() ln
ln![]() )′
= 3tg
)′
= 3tg![]() ln
ln![]() ·(tg
ln
·(tg
ln![]() )′
=
)′
=
=
3 tg![]() ln
ln![]() ·
· (ln
(ln![]() )′
=
)′
=
=
3 tg![]() ln
ln![]() ·
· ·
·![]() ·
· =
=
=
3 tg![]() ln
ln![]()
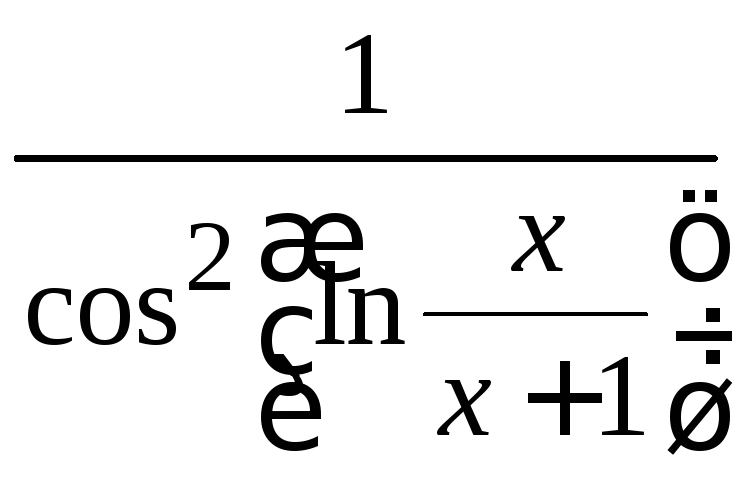 ·
·![]() ·
· =
=
=
3 tg![]() ln
ln![]() ·
·
![]() ·
·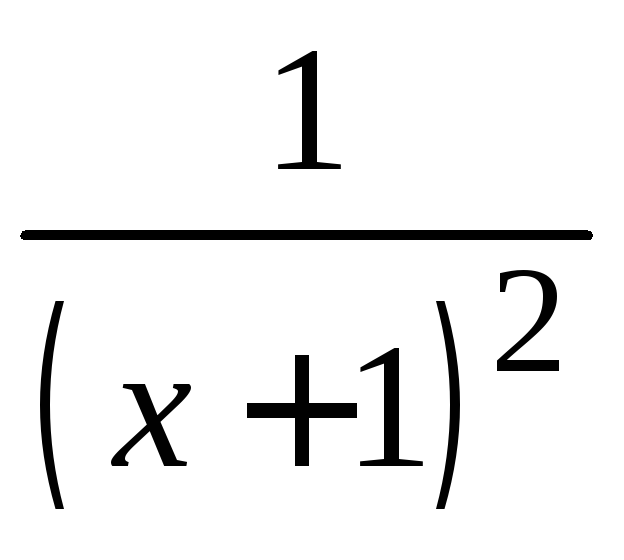 =
=
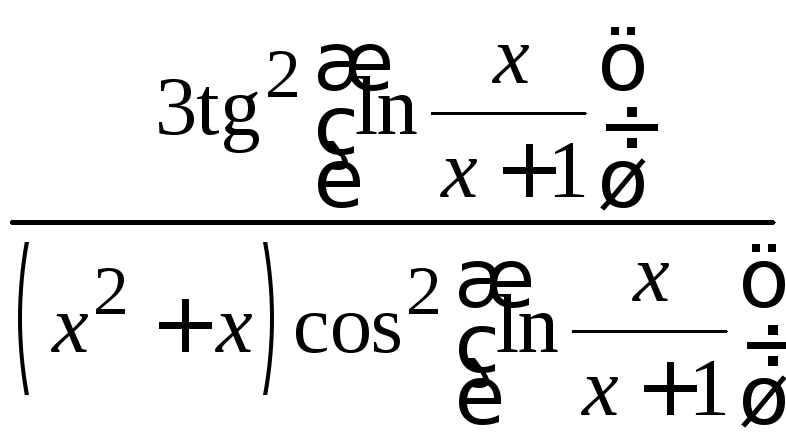 .
.
4.
Составить уравнения касательной и
нормали к графику функции
у
=
 в точке с абсциссойх
в точке с абсциссойх![]() =
2.
=
2.
Решение:
Уравнения касательной и нормали к
графику функции определяются формулами
(12.2) и (12.3). Вычислим сначала значения
функции и производной в точке х![]() :
:
у![]() = у(2)
=
= у(2)
=
![]() ,
,
у′
=
 =
= =
= ,
,
у′(2)
=
![]() .
.
Подставим найденные значения в формулу (12.2):
у
–
![]() =
=![]() (х
– 2).
(х
– 2).
Получаем уравнение касательной: 2х – 6у – 1 = 0.
Подставив теперь значения в формулу (12.3), получим уравнение нормали:
у
–
![]() = –3(х
– 2) или 6х
+ 2у
– 13 = 0.
= –3(х
– 2) или 6х
+ 2у
– 13 = 0.
Задачи для самостоятельного решения
1.
Закон движения точки есть s
= 2t![]() +
3t
+ 5, где расстояние s
дается
в сантиметрах и время t
– в секундах. Чему равна средняя скорость
точки за промежуток времени от t
= 1 до t
= 5?
+
3t
+ 5, где расстояние s
дается
в сантиметрах и время t
– в секундах. Чему равна средняя скорость
точки за промежуток времени от t
= 1 до t
= 5?
2.
Найти производную х′![]() ,
еслиу
= х
,
еслиу
= х![]() + ln
+ ln
![]() .
.
3. Найти производные следующих функций:
а)
y
=
 ,
б)
y
= sin(
,
б)
y
= sin(![]() +
+
![]() ),
),
в)
y
=ln ln![]() ln
ln![]() x,
г)
y
=
x,
г)
y
=

д)
y
=
 ,
е)
y
=
,
е)
y
=![]() cth
x
–
cth
x
–
 ,
,
ж)
y
=
![]() cos
tg 2 + e
cos
tg 2 + e![]() ,
з)
y
= ln
,
з)
y
= ln ,
,
и)
y
=
![]() ,
к) у
= x
,
к) у
= x![]() cos
α
+ sin
α
ln
sin(x
– α).
cos
α
+ sin
α
ln
sin(x
– α).
4. Найти производные следующих функций:
а)
y
=
![]() ;
б)
y
=
;
б)
y
= ;
;
в)
y
=
 ;
г)
y
= log
;
г)
y
= log![]() log
log![]() tg x;
tg x;
д)
y
= ;
е)
y
= arctg
;
е)
y
= arctg ;
;
ж)
y
=
![]() ;
з)
y
= ln(arccos(x
+ 1));
;
з)
y
= ln(arccos(x
+ 1));
и)
y
= cos![]()
![]() ;
к)
y
= x
;
к)
y
= x![]() (ln
(ln![]() )
– sin e
)
– sin e![]() ;
;
л)
y
=
 ; м)y
=
; м)y
=
![]() ln
tg
ln
tg
![]()
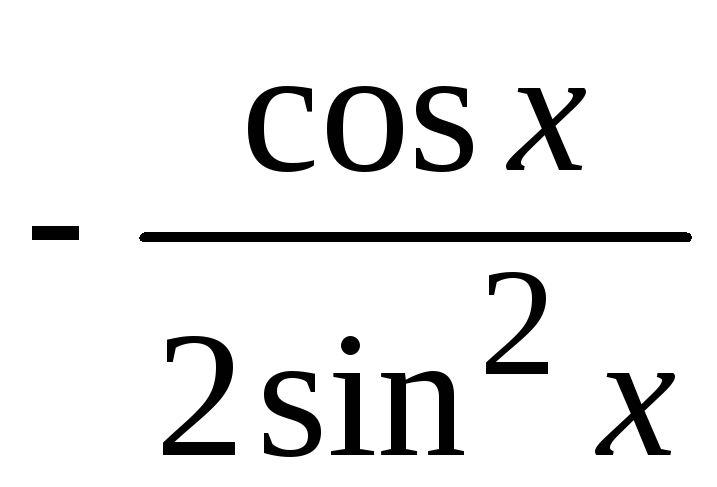 .
.
5. Составить уравнения касательной и нормали к кривым в указанных точках:
а)
у
= arcsin
![]() в точке пересечения с осью ОХ;
в точке пересечения с осью ОХ;
б)
у
= e![]() в точках пересечения с прямойу
= 1.
в точках пересечения с прямойу
= 1.
6.
Показать, что функция у
=
![]() удовлетворяет уравнениюxy′
= = y(yln
x
–
1).
удовлетворяет уравнениюxy′
= = y(yln
x
–
1).
Ответы:
1) 15 см/сек;
2) х′![]() =
= ;3) а)
;3) а) ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)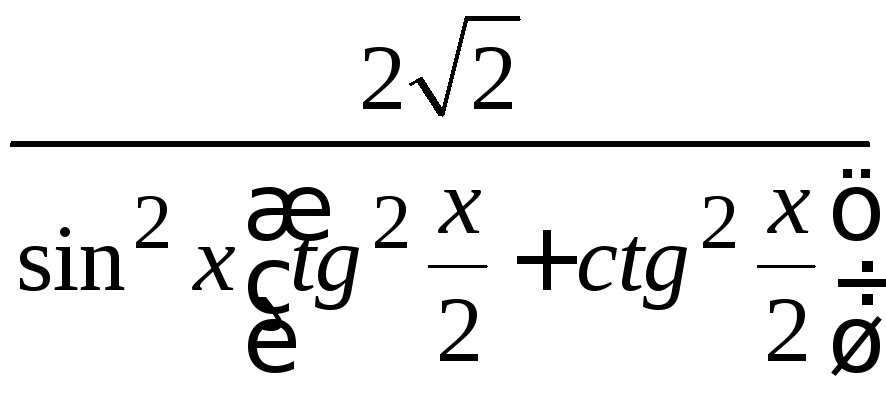 ;
д)
;
д)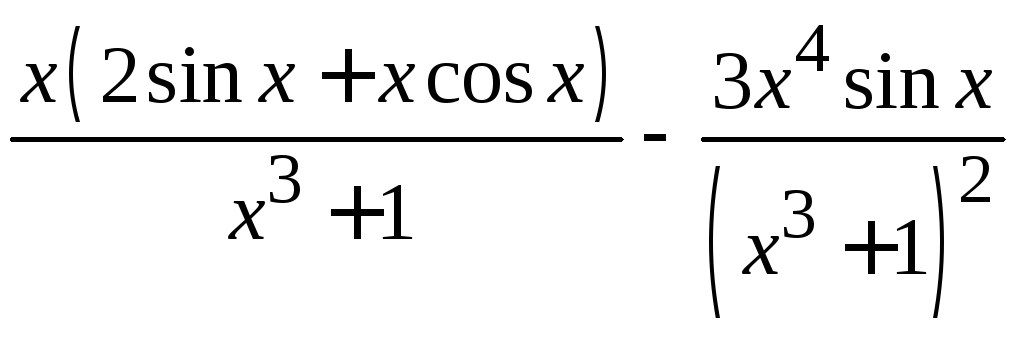 ;
е)
;
е) ;
ж)
;
ж) ;
з)
;
з) ;
и)
;
и) ;
к)
;
к)![]() ;4) а)
;4) а) 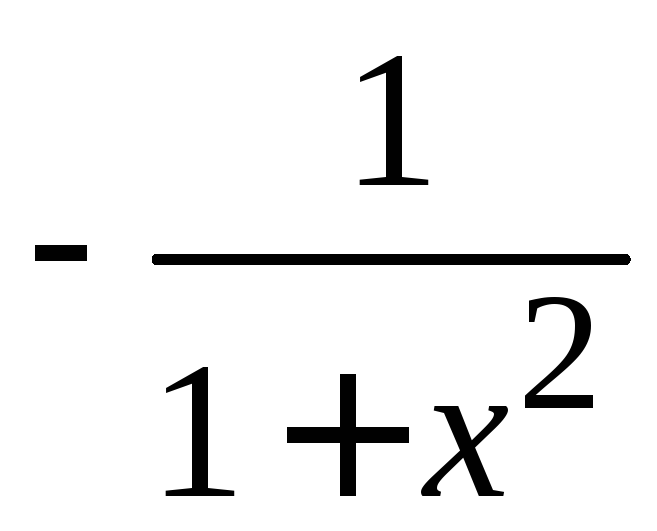 ;
б)
;
б)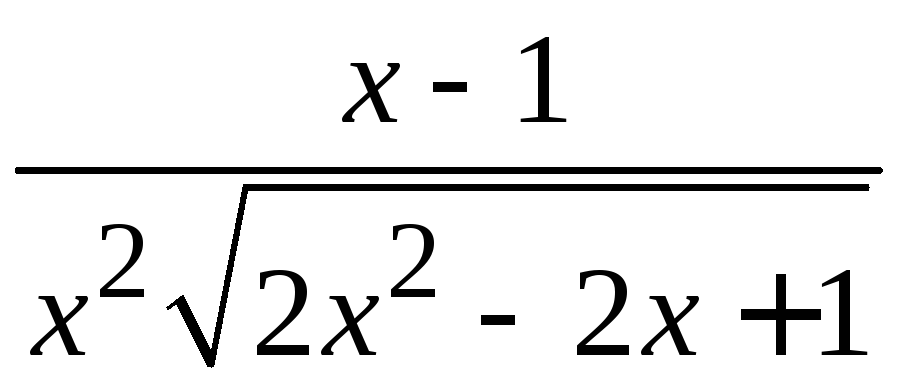 ;
в)
;
в) ;
г)
;
г) ;
д)
;
д) ;
е)
;
е) ;
ж)
;
ж)![]()
 ;
з)
;
з) ;
и)
;
и)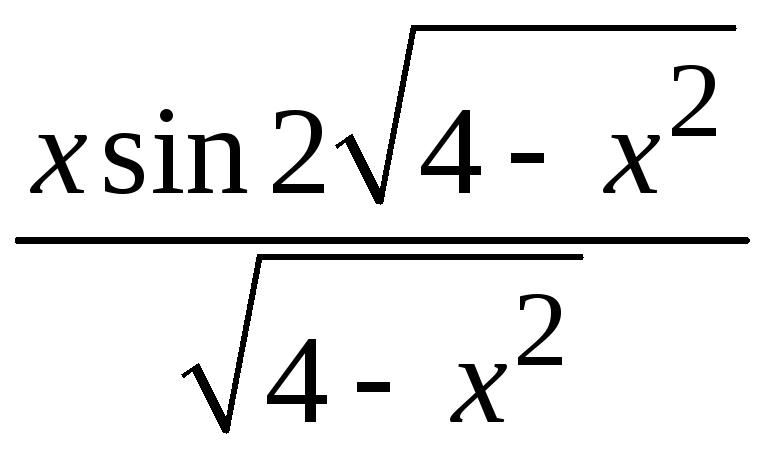 ;
к)
;
к) ;
л)
;
л) ;
м)
;
м) ;
5) 1)
;
5) 1)
![]() ,
,![]() ;
2)
;
2)![]() ,
,![]() для точки (1; 1),
для точки (1; 1),![]() ,
,![]() для точки (–1; 1).
для точки (–1; 1).
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 13
