
- •Вычисление определителей 2-го, 3-го и высших порядков
- •1. Определитель 2-го и 3-го порядков.
- •2. Определитель произвольного порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Действия над матрицами, вычисление обратной матрицы. Решение матричных уравнений
- •1. Алгебра матриц.
- •2. Обратная матрица.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Решение систем линейных уравнений методом Крамера и Гаусса
- •1. Метод Крамера.
- •2. Метод Гаусса.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Векторная алгебра. Вычисление координат, модуля и направляющих косинусов вектора
- •1. Векторная алгебра.
- •2. Деление отрезка в данном отношении.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Скалярное, векторное и смешанное произведения векторов
- •1. Скалярное произведение векторов.
- •2. Векторное произведение векторов.
- •3. Смешанное произведение векторов.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Прямая линия на плоскости
- •1. Общее уравнение прямой.
- •2. Уравнение прямой в отрезках.
- •3. Каноническое уравнение прямой.
- •6. Параметрические уравнения прямой.
- •7. Прямая с угловым коэффициентом.
- •8. Нормальное уравнение прямой.
- •10. Условия параллельности и перпендикулярности прямых. Нахождение угла между прямыми.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Плоскость и прямая в пространстве
- •1. Общее уравнение плоскости.
- •2. Уравнение плоскости в отрезках.
- •3. Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой.
- •5. Уравнение плоскости, параллельной двум неколлинеарным векторам и проходящей через точку.
- •7. Нормальное уравнение плоскости.
- •9. Общие уравнения прямой.
- •10. Канонические уравнения прямой.
- •12. Параметрические уравнения прямой.
- •13. Взаимное расположение прямых и плоскостей.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Кривые второго порядка
- •1. Эллипс.
- •2. Гипербола.
- •3. Парабола.
- •4. Единое определение кривой второго порядка.
- •5. Полярное уравнение кривой второго порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Предел числовой последовательности. Предел функции
- •1. Предел числовой последовательности.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Раскрытие неопределенностей. Замечательные пределы
- •1. Замечательные пределы.
- •2. Сравнение бесконечно малых.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Непрерывность функции. Точки разрыва функции
- •1. Непрерывность функции.
- •2. Точки разрыва.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вычисление производных
- •1. Производная и ее геометрический и механический смысл.
- •3. Производные основных элементарных функций.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Производная неявной, параметрически заданной и сложно-степенной функции
- •Задачи для самостоятельного решения
- •Производные высших порядков. Дифференциал функции. Приложения дифференциалов
- •1. Производные высших порядков.
- •2. Дифференциал функции.
- •3. Формула приближенного вычисления.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Правило Лопиталя. Точки экстремума функции.
- •1. Правило Лопиталя.
- •2. Возрастание и убывание функции.
- •3. Точки экстремума функции.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Исследование функций и построение графиков
- •1. Выпуклость и вогнутость функции.
- •2. Точки перегиба функции.
- •3. Асимптоты функции.
- •4. Общий план исследования функции и построение графика.
- •Примеры решения задач
- •Задачи для самостоятельного решения
2. Точки разрыва.
Если функция определена в некоторой окрестности точки а, но не является непрерывной в этой точке, то говорят, что она имеет разрыв в этой точке, точка а при этом называется точкой разрыва функции f (x).
Приведем классификацию точек разрыва функции.
Точка разрыва х = а функции
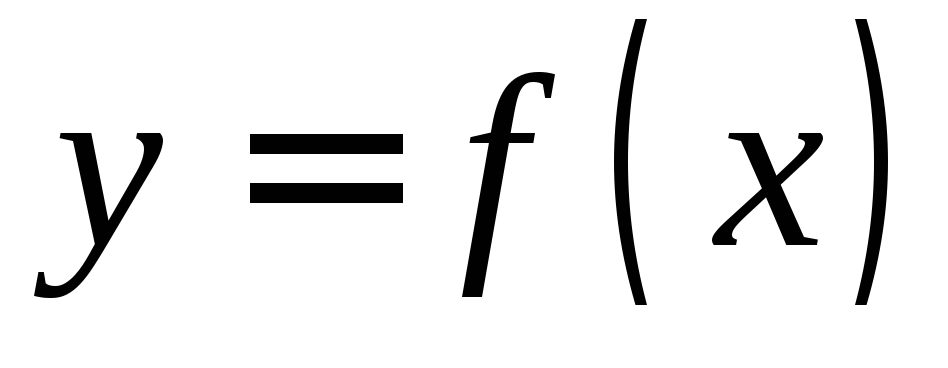 называетсяточкой
разрыва
первого
рода,
если существуют конечные пределы
называетсяточкой
разрыва
первого
рода,
если существуют конечные пределы
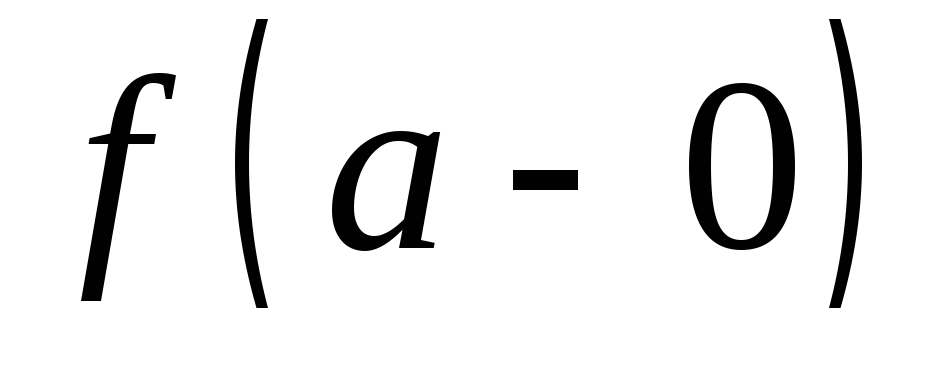 ,
,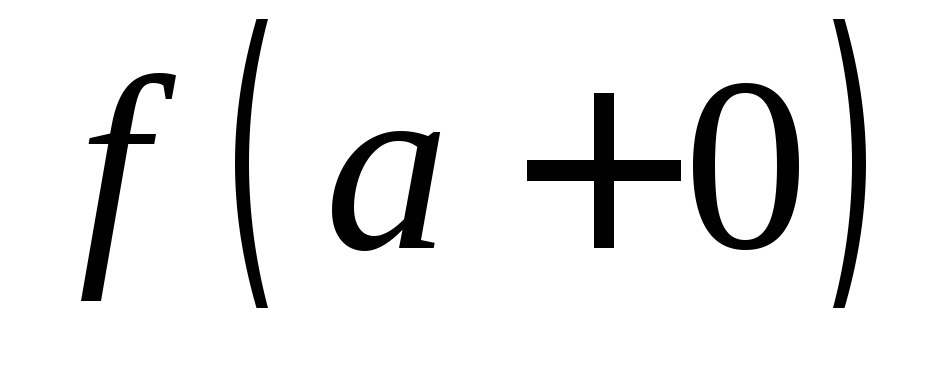 ,
но функция все же разрывна ва.
,
но функция все же разрывна ва.
а – точка скачка функции
 ,
если
,
если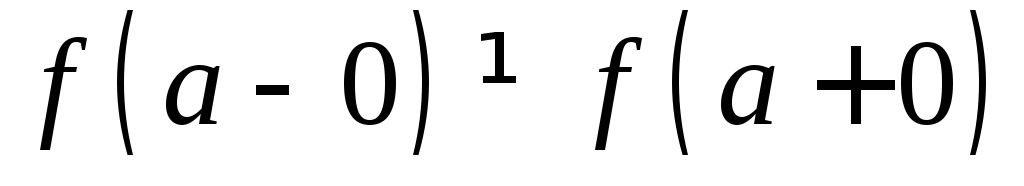 (см. рис. 11.2),
(см. рис. 11.2),а – точка устранимого разрыва функции
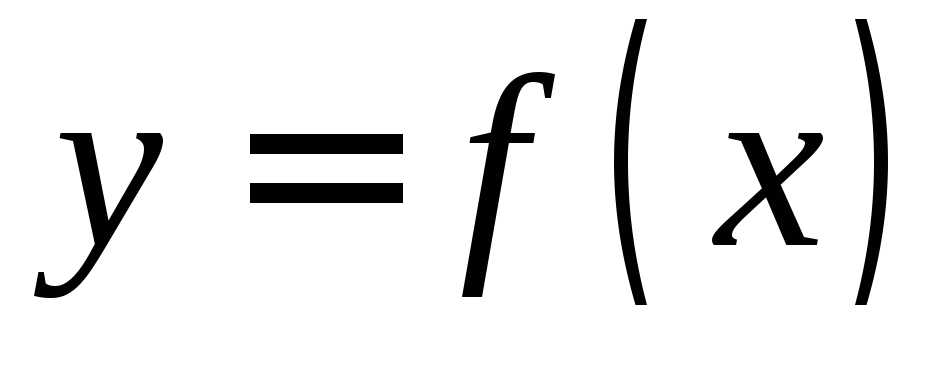 ,
если скачок
,
если скачок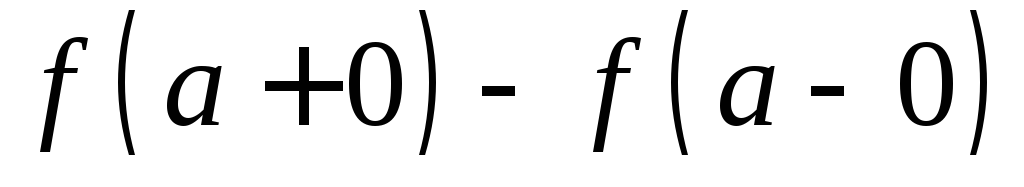 равен нулю, т.е.
равен нулю, т.е. (см. рис. 11.3).
(см. рис. 11.3).
Точка разрыва х = а функции
 называетсяточкой
разрыва
второго
рода,
если а
не является точкой разрыва первого
рода, т.е. если равен бесконечности или
не существует хотя бы один из односторонних
пределов
называетсяточкой
разрыва
второго
рода,
если а
не является точкой разрыва первого
рода, т.е. если равен бесконечности или
не существует хотя бы один из односторонних
пределов
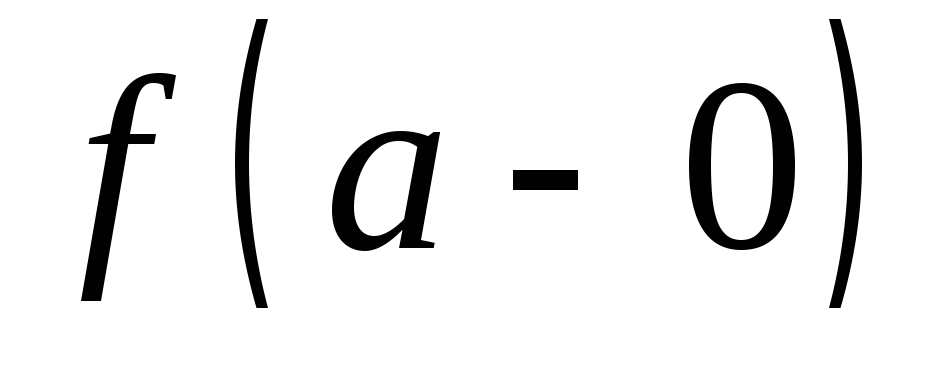 ,
, .
.а – точка бесконечного разрыва функции
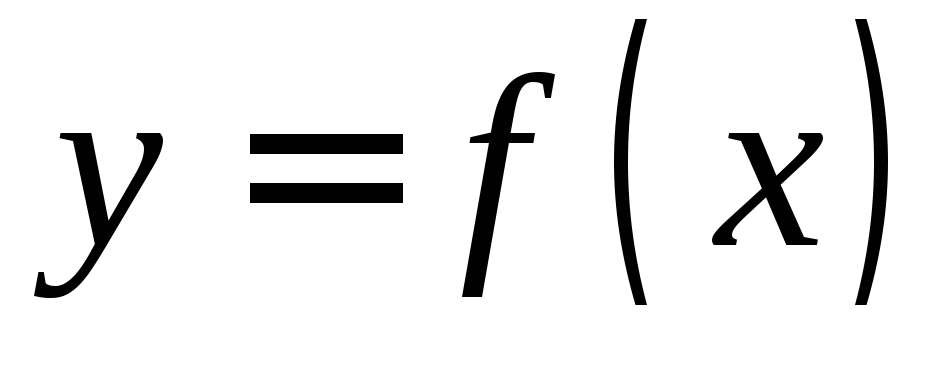 ,
если пределы
,
если пределы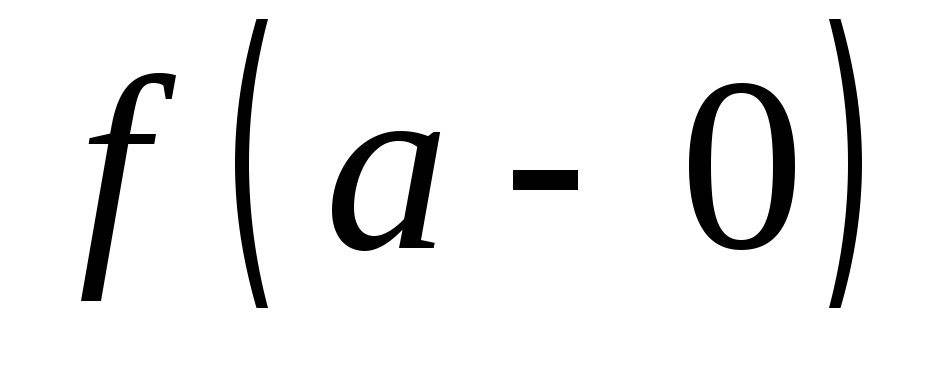 и
и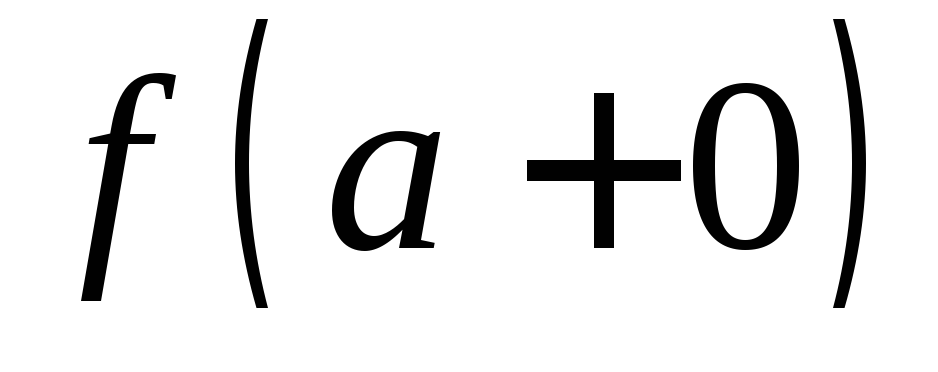 существуют, но хотя бы один из них
бесконечный (см. рис. 11.4).
существуют, но хотя бы один из них
бесконечный (см. рис. 11.4).


Рис. 11.2 Рис. 11.3

Рис. 11.4
Примеры решения задач
Установить
характер точки разрыва функции
![]() в точке
в точке![]() или доказать непрерывность функции в
этой точке:
или доказать непрерывность функции в
этой точке:
1.
![]() ;
2.
;
2. 3.
3. ;
;
4.
 ;
5.
;
5.![]()
Решение:
1.
При
![]() функция
функция![]() не определена, следовательно, она не
непрерывна в этой точке. Так как
не определена, следовательно, она не
непрерывна в этой точке. Так как![]() то
то![]() – точка устранимого разрываI
рода.
– точка устранимого разрываI
рода.
2.
По сравнению с первым примером функция
 доопределена в точке
доопределена в точке![]() так, что
так, что![]() следовательно, данная функция непрерывна
в этой точке.
следовательно, данная функция непрерывна
в этой точке.
3.
При
![]() функция
функция не определена. Так как пределы функции
слева и справа от точки
не определена. Так как пределы функции
слева и справа от точки![]() конечны и различны:
конечны и различны:
 ,
,
то
в точке
![]() функция имеет разрывI
рода.
функция имеет разрывI
рода.
4.
При х = 0
функция
 не определена;
не определена;
 ,
, .Так
как один из односторонних пределов
бесконечен, то
.Так
как один из односторонних пределов
бесконечен, то
![]() – точка разрыва II
рода.
– точка разрыва II
рода.
5.
При х
= 0 функция
 не определена. Так как односторонние
пределы
не определена. Так как односторонние
пределы
![]() не существуют (значения функции колеблются
от –1 до 1 и от 1 до –1, не стремясь ни к
какому числу), то х
= 0 – точка разрыва II
рода.
не существуют (значения функции колеблются
от –1 до 1 и от 1 до –1, не стремясь ни к
какому числу), то х
= 0 – точка разрыва II
рода.
Задачи для самостоятельного решения
Какие из следующих функций являются непрерывными в точке х = –1? В случае нарушения непрерывности установить характер точки разрыва:
1.
![]() ;
2.
;
2.

3.
![]() ;
4.
;
4.
![]() ;
;
5.
 ;
6.
;
6.
![]()
Исследовать на непрерывность функцию, найти точки разрыва и указать характер разрыва:
7.
 8.
8.

9.
![]() 10.
10.
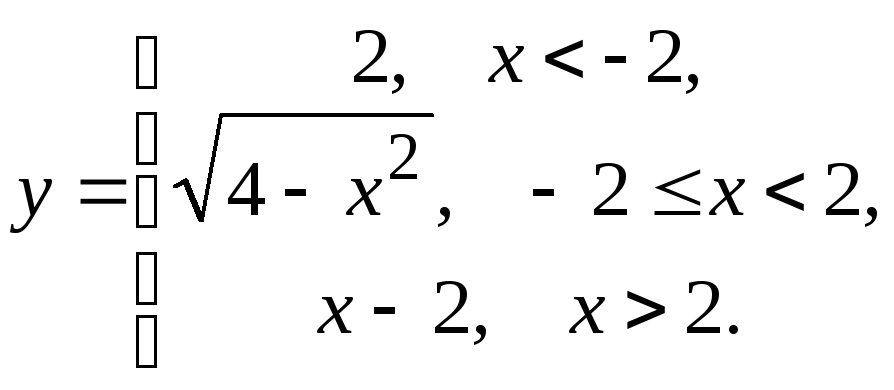
Ответы:
1)
Точка устранимого разрыва I
рода; 2)
непрерывна; 3)
точка разрыва II
рода; 4)
точка разрыва II
рода; 5)
точка разрыва I
рода; 6)
точка разрыва I
рода; 7)
x
= 0 – точка устранимого разрыва I
рода; 8)
x
= –π – точка разрыва I
рода, в точке x
=
![]() функция непрерывна; 9)
x
= –2 – точка разрыва I
рода; 10)
x
=
–2 – точка разрыва первого рода, x
= 2 – точка устранимого разрыва I
рода.
функция непрерывна; 9)
x
= –2 – точка разрыва I
рода; 10)
x
=
–2 – точка разрыва первого рода, x
= 2 – точка устранимого разрыва I
рода.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 12
Вычисление производных
1. Производная и ее геометрический и механический смысл.
Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
![]() (12.1)
(12.1)
Используя определение производной, можно находить производную любой функции по схеме:
1) аргументу х даем приращение x 0 и находим для функции у соответствующее значение у + у в точке х + х;
2) получаем у;
3)
составляем отношение
![]() ;
;
4)
находим предел отношения при x
0, получаем производную
![]()
Геометрический
смысл:
если f
(х)
непрерывная функция в точке
![]() ,
то производная функции в точке
,
то производная функции в точке![]() (если она существует) равна тангенсу
угла наклона касательной к осиОх,
в точке
(если она существует) равна тангенсу
угла наклона касательной к осиОх,
в точке
![]() .
Причем функция имеет производную в
точке
.
Причем функция имеет производную в
точке![]() тогда и только тогда, когда в этой точке
существует касательная к графику
функции.
тогда и только тогда, когда в этой точке
существует касательная к графику
функции.
Уравнение
касательной
к графику функции
f (х)
в точке
![]() :
:
![]() (12.2)
(12.2)
Уравнение
нормали
к графику функции
f (х)
в точке
![]() :
:
 (12.3)
(12.3)
Механический
смысл:
если
f (t)
выражает зависимость пройденного пути
движущейся точки от времени t,
то скорость точки есть производная от
пути по времени:
![]() .
.
2. Правила дифференцирования.
1)
Производная константы равна нулю:
![]() .
.
2)
Константа выносится за знак производной:
![]() .
.
3)
Производная суммы функций:
![]() .
.
4) Производная произведения функций:
![]() .
(12.4)
.
(12.4)
5) Производная частного:
 .
(12.5)
.
(12.5)
6) Пусть дана сложная функция у = f (u), где и = g (x) и пусть функция u = g (x) имеет производную в точке х, а функция y = f (u) имеет производную в точке и = g (x). Тогда сложная функция у = f (g(х)) имеет производную в точке х и
![]() (12.6)
(12.6)
