
- •Вычисление определителей 2-го, 3-го и высших порядков
- •1. Определитель 2-го и 3-го порядков.
- •2. Определитель произвольного порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Действия над матрицами, вычисление обратной матрицы. Решение матричных уравнений
- •1. Алгебра матриц.
- •2. Обратная матрица.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Решение систем линейных уравнений методом Крамера и Гаусса
- •1. Метод Крамера.
- •2. Метод Гаусса.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Векторная алгебра. Вычисление координат, модуля и направляющих косинусов вектора
- •1. Векторная алгебра.
- •2. Деление отрезка в данном отношении.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Скалярное, векторное и смешанное произведения векторов
- •1. Скалярное произведение векторов.
- •2. Векторное произведение векторов.
- •3. Смешанное произведение векторов.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Прямая линия на плоскости
- •1. Общее уравнение прямой.
- •2. Уравнение прямой в отрезках.
- •3. Каноническое уравнение прямой.
- •6. Параметрические уравнения прямой.
- •7. Прямая с угловым коэффициентом.
- •8. Нормальное уравнение прямой.
- •10. Условия параллельности и перпендикулярности прямых. Нахождение угла между прямыми.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Плоскость и прямая в пространстве
- •1. Общее уравнение плоскости.
- •2. Уравнение плоскости в отрезках.
- •3. Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой.
- •5. Уравнение плоскости, параллельной двум неколлинеарным векторам и проходящей через точку.
- •7. Нормальное уравнение плоскости.
- •9. Общие уравнения прямой.
- •10. Канонические уравнения прямой.
- •12. Параметрические уравнения прямой.
- •13. Взаимное расположение прямых и плоскостей.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Кривые второго порядка
- •1. Эллипс.
- •2. Гипербола.
- •3. Парабола.
- •4. Единое определение кривой второго порядка.
- •5. Полярное уравнение кривой второго порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Предел числовой последовательности. Предел функции
- •1. Предел числовой последовательности.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Раскрытие неопределенностей. Замечательные пределы
- •1. Замечательные пределы.
- •2. Сравнение бесконечно малых.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Непрерывность функции. Точки разрыва функции
- •1. Непрерывность функции.
- •2. Точки разрыва.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вычисление производных
- •1. Производная и ее геометрический и механический смысл.
- •3. Производные основных элементарных функций.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Производная неявной, параметрически заданной и сложно-степенной функции
- •Задачи для самостоятельного решения
- •Производные высших порядков. Дифференциал функции. Приложения дифференциалов
- •1. Производные высших порядков.
- •2. Дифференциал функции.
- •3. Формула приближенного вычисления.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Правило Лопиталя. Точки экстремума функции.
- •1. Правило Лопиталя.
- •2. Возрастание и убывание функции.
- •3. Точки экстремума функции.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Исследование функций и построение графиков
- •1. Выпуклость и вогнутость функции.
- •2. Точки перегиба функции.
- •3. Асимптоты функции.
- •4. Общий план исследования функции и построение графика.
- •Примеры решения задач
- •Задачи для самостоятельного решения
Задачи для самостоятельного решения
Доказать, используя определение предела, что:
1.
![]() ;
2.
;
2.![]() .
.
Найти пределы:
3.
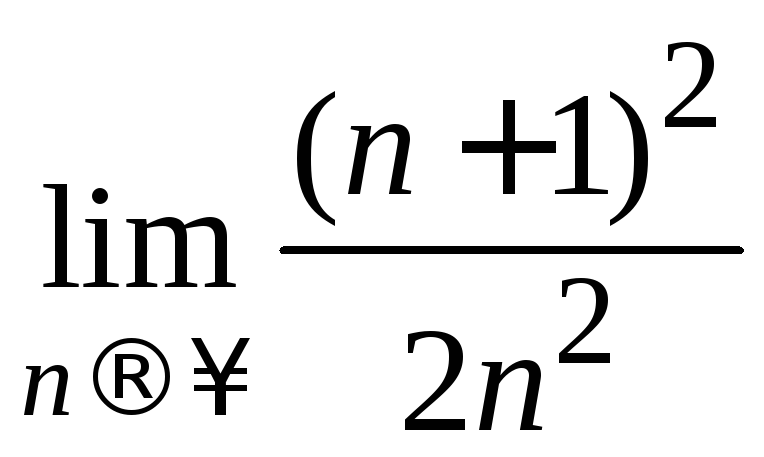 ;
4.
;
4. ;
;
5.
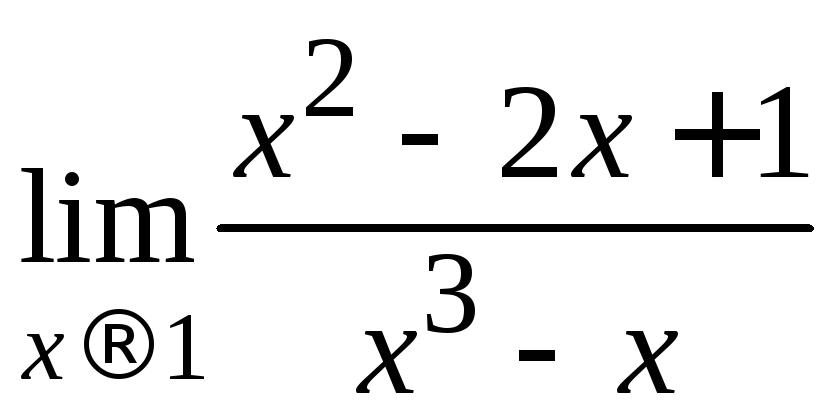 ; 6.
; 6. ;
;
7.
 ;
8.
;
8. ;
;
9.
 ;
10.
;
10.![]() ;
;
11.
 ; 12.
; 12. ;
;
13.
![]() ; 14.
; 14. ;
;
15.
 ;
16.
;
16. ;
;
17.![]() ;18.
;18. ;
;
19.
 ;
20.
;
20. ;
;
21.
![]() ; 22.
; 22. .
.
Ответы:
3)
![]() ;4)
48; 5)
0; 6)
;4)
48; 5)
0; 6)
![]() ;7)
;7)
![]() ;8)
;8)
![]() ;9)
;9)
![]() при
при![]() и2
при
и2
при
![]() ;10)
0; 11)
;10)
0; 11)
![]() ;12)
0; 13)
;12)
0; 13)
![]() ;14)
0; 15)
1; 16)
;14)
0; 15)
1; 16)
![]() ;17)
;17)
![]() ;
18)
;
18)
![]() ;19)
;19) ![]() ;20)
4; 21)
;20)
4; 21)
![]() ;
22)
;
22)
![]() .
.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 10
Раскрытие неопределенностей. Замечательные пределы
1. Замечательные пределы.
Первый
замечательный предел:
![]() (10.1)
(10.1)
Второй замечательный предел записывается в двух видах:
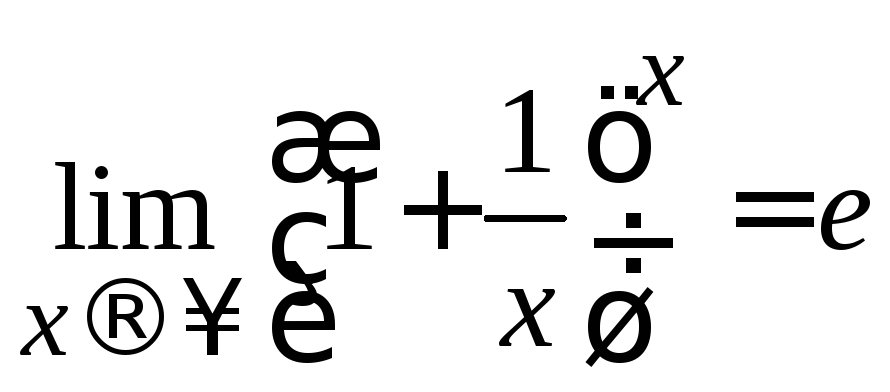
![]() (10.2)
(10.2)
2. Сравнение бесконечно малых.
Две
бесконечно малые
![]() и
и![]() называютсявеличинами
одного и того же порядка малости
при
называютсявеличинами
одного и того же порядка малости
при
![]() ,
если
,
если
 В частности, если
k
= 1,
то говорят, что
В частности, если
k
= 1,
то говорят, что
![]() и
и![]() эквивалентные
величины
и пишут
эквивалентные
величины
и пишут
![]() .
Таким образом,
.
Таким образом,
 .
.
Теорема.
Пусть
![]() при
при![]() ,
тогда справедливы равенства:
,
тогда справедливы равенства:
 ,
,
 ,
,
![]() ,
,
где
![]() – некоторая функция, определенная в
окрестности точкиа.
– некоторая функция, определенная в
окрестности точкиа.
Для
применения этой теоремы на практике
полезно знать как можно больше пар
эквивалентных функций. Например, из
первого замечательного предела следует,
что
![]() .
Приведем еще несколько наиболее часто
используемых эквивалентностей.
.
Приведем еще несколько наиболее часто
используемых эквивалентностей.
 (10.3)
(10.3)
Примеры решения задач
1. Вычислить:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в) ;
г)
;
г)![]() .
.
Решение:
а)
 ,
,
здесь
мы сделали замену
![]() ,
при
,
при![]() ,
и использовали первый замечательный
предел (10.1).
,
и использовали первый замечательный
предел (10.1).
б)
 .
.
в)
 .
.
г)
При
![]() имеем неопределенность вида
имеем неопределенность вида![]() .
Сделаем замену
.
Сделаем замену![]() ,
тогда
,
тогда![]() и при
и при![]() ,
получаем:
,
получаем:

 .
.
2.Вычислить:
а)
 ;
б)
;
б)![]() ;
в)
;
в) .
.
Решение:
а)
Имеем неопределенность вида
![]() .
Выделим у дроби целую часть
.
Выделим у дроби целую часть![]() .
Обозначим
.
Обозначим![]() ;
при
;
при![]() ,
причем
,
причем![]() .
Получаем:
.
Получаем:
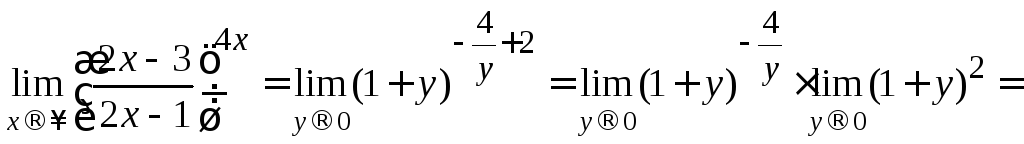
 .
.
Здесь мы использовали второй замечательный предел (10.2).
б)
Имеем неопределенность вида
![]() ,
т. к.
,
т. к.

Перейдем к пределу под знаком логарифма:
 .
.
в)
Имеем неопределенность вида
![]() .
Преобразуя выражение и используя
непрерывность показательно-степенной
функции и второй замечательный предел
(10.2), получаем:
.
Преобразуя выражение и используя
непрерывность показательно-степенной
функции и второй замечательный предел
(10.2), получаем:
 .
.
3. Вычислить:
а)
 ;
б)
;
б) .
.
Решение:
а)
Имеем неопределенность вида ![]() .
Используем первую эквивалентность из
таблицы (10.3) и заменяем
.
Используем первую эквивалентность из
таблицы (10.3) и заменяем
![]() на
на![]() :
:
 .
.
б)
Используем формулы 5) и 8) из таблицы
(10.3). Заменяя бесконечно малые
![]() на
на ,
соответственно, получаем
,
соответственно, получаем
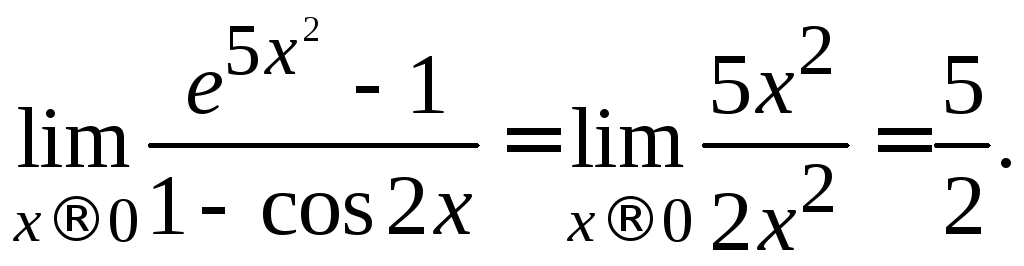
Задачи для самостоятельного решения
Вычислить:
1.
![]() ;
2.
;
2.![]() ;
;
3.
![]() ;
4.
;
4.![]() ;
;
5.
 ;
6.
;
6. ;
;
7.
 ; 8.
; 8.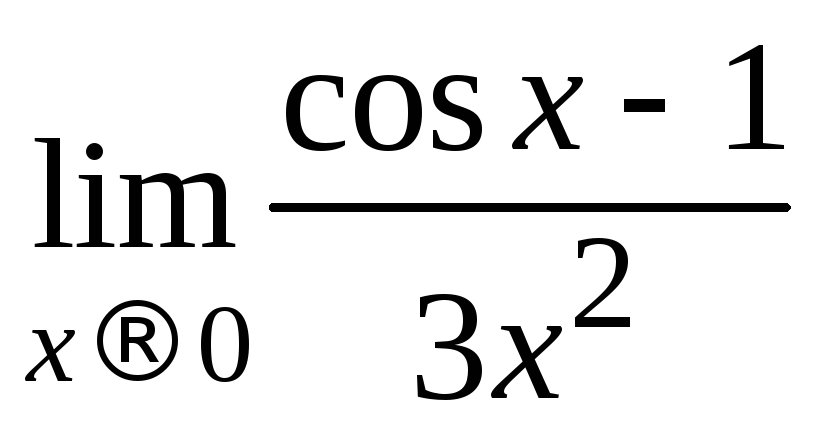 ;
;
9.
 ;
10.
;
10.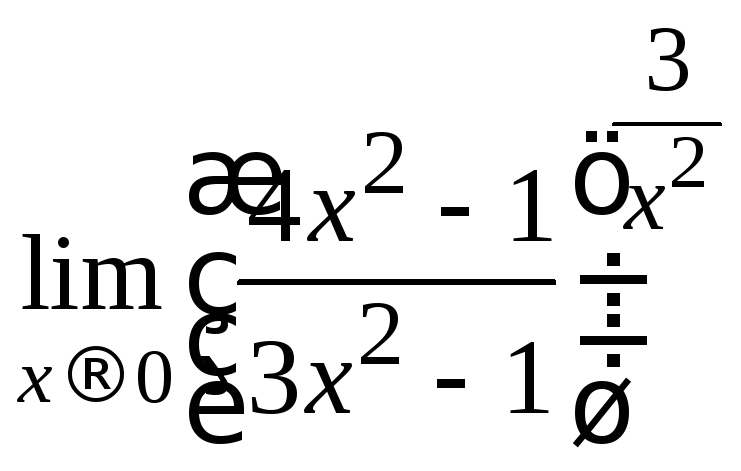 ;
;
11.
![]() ;
12.
;
12. ;
;
13.
 ;
14.
;
14.![]() ;
;
15.
![]() ;
16.
;
16. ;
;
17.
 ;
18.
;
18. ;
;
19.
 ;
20.
;
20. .
.
Найти пределы следующих функций с помощью эквивалентных бесконечно малых:
21.
 ;
22.
;
22. ;
;
23.
![]() ;
24.
;
24. ;
;
25.
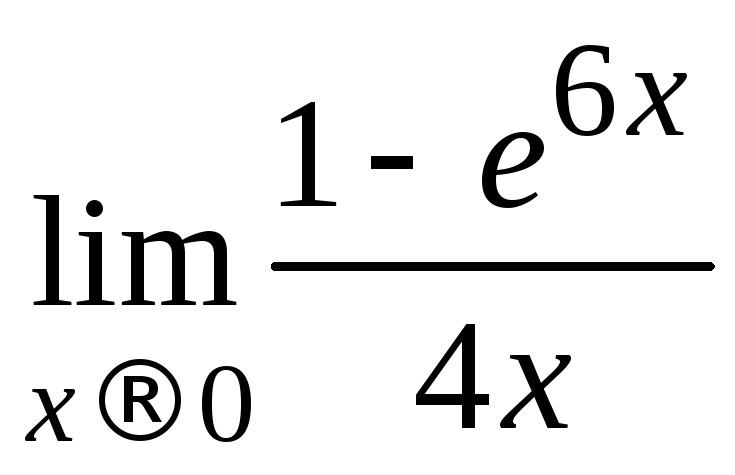 .
.
Ответы:
1)
![]() ;2)
;2)
![]() ;3)
;3)
![]() ;4)
;4)
![]() ;5)
;5)
![]() ;6)
;6)
![]() ;7)
6,4; 8)
;7)
6,4; 8)
![]() ;9)
0; 10)
;9)
0; 10)
![]() ;11) 0,05;
12)
0,125; 13)
0; 14)
0; 15)
0,3; 16)
1; 17)
2; 18)
;11) 0,05;
12)
0,125; 13)
0; 14)
0; 15)
0,3; 16)
1; 17)
2; 18)
![]() ;19)
0,1;
20)
1; 21)
;19)
0,1;
20)
1; 21) ![]() ;22)
64; 23)
30; 24)
4,5; 25)
1,5.
;22)
64; 23)
30; 24)
4,5; 25)
1,5.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 11
Непрерывность функции. Точки разрыва функции
1. Непрерывность функции.
Приведем три эквивалентных определения функции, непрерывной в точке.
1. Функция y = f(x), определённая в некоторой окрестности точки а и в самой этой точке, называется непрерывной в точке a, если
![]() .
.
2. Функция у = f(x), определённая в некоторой окрестности точки а и в самой этой точке, называется непрерывной в точке а, если > 0 > 0 x
|
x
– a
|
<
![]() |
f(x)
– f(a)
|
< .
|
f(x)
– f(a)
|
< .
3. Функция у = f(x), определённая в некоторой окрестности точки а и в самой этой точке, называется непрерывной в точке а, если приращение функции у = f (a + x) – f(a) в точке а стремится к нулю, когда приращение аргумента х = х – а стремится к нулю (см. рис. 11.1), т.е.
![]() .
.
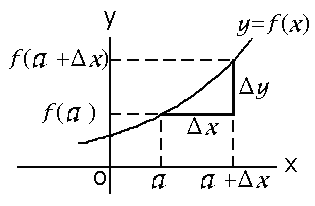
Рис. 11.1
