
- •Вычисление определителей 2-го, 3-го и высших порядков
- •1. Определитель 2-го и 3-го порядков.
- •2. Определитель произвольного порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Действия над матрицами, вычисление обратной матрицы. Решение матричных уравнений
- •1. Алгебра матриц.
- •2. Обратная матрица.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Решение систем линейных уравнений методом Крамера и Гаусса
- •1. Метод Крамера.
- •2. Метод Гаусса.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Векторная алгебра. Вычисление координат, модуля и направляющих косинусов вектора
- •1. Векторная алгебра.
- •2. Деление отрезка в данном отношении.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Скалярное, векторное и смешанное произведения векторов
- •1. Скалярное произведение векторов.
- •2. Векторное произведение векторов.
- •3. Смешанное произведение векторов.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Прямая линия на плоскости
- •1. Общее уравнение прямой.
- •2. Уравнение прямой в отрезках.
- •3. Каноническое уравнение прямой.
- •6. Параметрические уравнения прямой.
- •7. Прямая с угловым коэффициентом.
- •8. Нормальное уравнение прямой.
- •10. Условия параллельности и перпендикулярности прямых. Нахождение угла между прямыми.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Плоскость и прямая в пространстве
- •1. Общее уравнение плоскости.
- •2. Уравнение плоскости в отрезках.
- •3. Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой.
- •5. Уравнение плоскости, параллельной двум неколлинеарным векторам и проходящей через точку.
- •7. Нормальное уравнение плоскости.
- •9. Общие уравнения прямой.
- •10. Канонические уравнения прямой.
- •12. Параметрические уравнения прямой.
- •13. Взаимное расположение прямых и плоскостей.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Кривые второго порядка
- •1. Эллипс.
- •2. Гипербола.
- •3. Парабола.
- •4. Единое определение кривой второго порядка.
- •5. Полярное уравнение кривой второго порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Предел числовой последовательности. Предел функции
- •1. Предел числовой последовательности.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Раскрытие неопределенностей. Замечательные пределы
- •1. Замечательные пределы.
- •2. Сравнение бесконечно малых.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Непрерывность функции. Точки разрыва функции
- •1. Непрерывность функции.
- •2. Точки разрыва.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вычисление производных
- •1. Производная и ее геометрический и механический смысл.
- •3. Производные основных элементарных функций.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Производная неявной, параметрически заданной и сложно-степенной функции
- •Задачи для самостоятельного решения
- •Производные высших порядков. Дифференциал функции. Приложения дифференциалов
- •1. Производные высших порядков.
- •2. Дифференциал функции.
- •3. Формула приближенного вычисления.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Правило Лопиталя. Точки экстремума функции.
- •1. Правило Лопиталя.
- •2. Возрастание и убывание функции.
- •3. Точки экстремума функции.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Исследование функций и построение графиков
- •1. Выпуклость и вогнутость функции.
- •2. Точки перегиба функции.
- •3. Асимптоты функции.
- •4. Общий план исследования функции и построение графика.
- •Примеры решения задач
- •Задачи для самостоятельного решения
Предел числовой последовательности. Предел функции
1. Предел числовой последовательности.
Число
а
называется пределом
числовой последовательности
![]() ,
если для любого
>
0
найдётся натуральное число N
такое, что
п
> N выполняется
неравенство | хn
- а
| < .
Или, используя краткую запись,
,
если для любого
>
0
найдётся натуральное число N
такое, что
п
> N выполняется
неравенство | хn
- а
| < .
Или, используя краткую запись,
> 0 N n > N | хn - а | < . (9.1)
В
этом случае пишут
![]() или
хn
а
и говорят, что хn
стремится к а
или
последовательность
или
хn
а
и говорят, что хn
стремится к а
или
последовательность
![]() сходится ка.
сходится ка.
Если
последовательность
![]() имеет
конечный предел, то говорят, что она
сходится.
Если последовательность не имеет
конечного предела, то ее называют
расходящейся.
имеет
конечный предел, то говорят, что она
сходится.
Если последовательность не имеет
конечного предела, то ее называют
расходящейся.
Арифметические свойства пределов последовательностей:
Пусть
![]()
a,
a,
![]()
b,
тогда
b,
тогда
1.
![]()
![]()
a
b,
a
b,
2.
![]()
![]()
a
b,
a
b,
3.
![]()
![]()
a
b,
b
0.
a
b,
b
0.
2. Предел функции.
Число b называют пределом функции f(x) при х а, если
> 0 > 0 x
|
x
– a
|
<
![]() |
f(x)
– b
|
< .
(9.2)
|
f(x)
– b
|
< .
(9.2)
Определение предела говорит о том, что если х приближается к а по любому закону, оставаясь не равным а, то f(x) приближается к b, делается как угодно близким к b.
Справедливы следующие свойства предела функции.
Если функция имеет предел при х а, то он единственен.
Арифметические свойства пределов: пусть
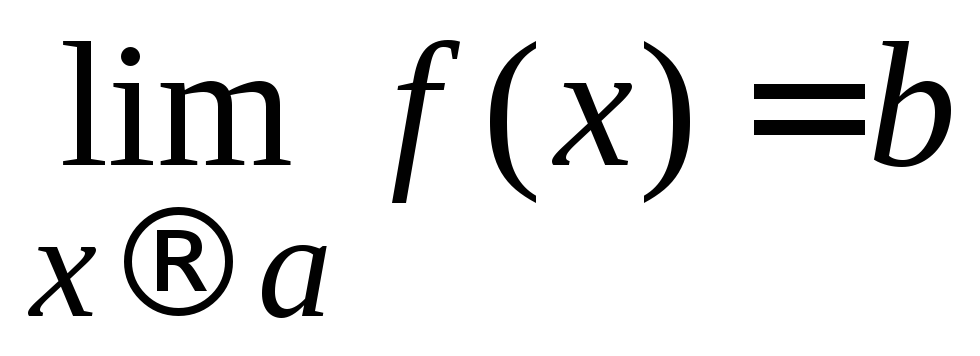 ,
, ,
гдеb
и
с
– конечные числа, тогда
,
гдеb
и
с
– конечные числа, тогда
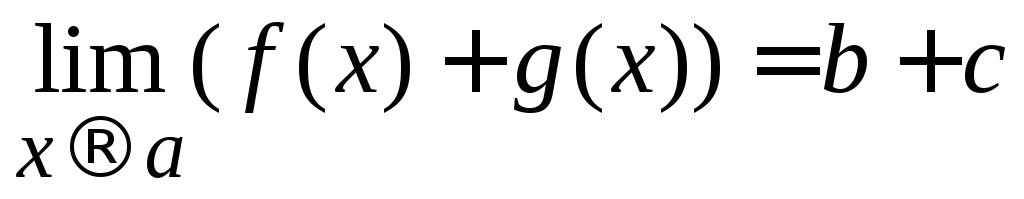 ,
,
 ,
,
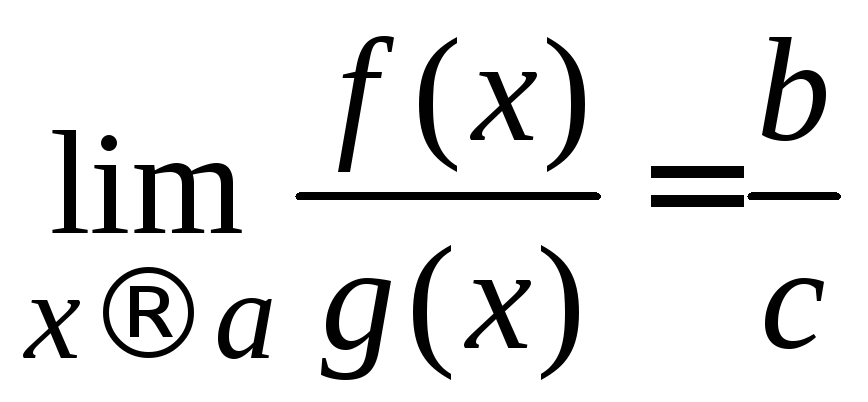 ,
если
c
0.
,
если
c
0.
Примеры решения задач
1.
Показать, используя определение предела
последовательности (9.1), что при n→![]() последовательность
последовательность![]() имеет
пределом число
имеет
пределом число![]() .
.
Решение:
Здесь х![]() –
–![]() =
=![]() –
–![]() =
=![]() .
Определим, при каком значенииn
выполняется равенство
.
Определим, при каком значенииn
выполняется равенство
![]() <
<![]() ;
так как
;
так как![]() >
>![]() ,
тоn
>
,
тоn
>
![]() .
Итак, если
.
Итак, если![]() ,
то приn
> N
выполняется неравенство
,
то приn
> N
выполняется неравенство
![]() <
<![]() ,
т. е.
,
т. е.![]() .
.
Так,
например, при
![]() = 0,1, заключаем, что неравенство
= 0,1, заключаем, что неравенство![]() < 0,1 выполняется приn
> N
= 13. Аналогично, неравенство
< 0,1 выполняется приn
> N
= 13. Аналогично, неравенство
![]() < 0,01 выполняется приn
> N
= 125.
< 0,01 выполняется приn
> N
= 125.
2.
Доказать, используя определение предела
последовательности (9.1), что
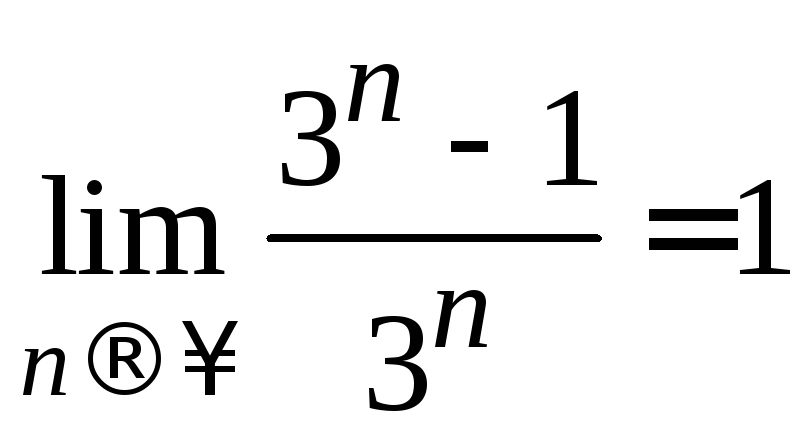 .
.
Решение:
Имеем для любого
![]()
0:
0:
![]() =
=![]() =
=![]()
![]() ,
следовательно,
,
следовательно,![]()
![]() или
или![]()
![]() ,
отсюда получаем
,
отсюда получаем![]()
![]() .
Таким образом, если выбрать
.
Таким образом, если выбрать ,
то при
,
то при![]() N
будет выполняться неравенство
N
будет выполняться неравенство
![]()
![]() .
Следовательно,
.
Следовательно, .
.
3.
Доказать, используя определение предела
функции (9.2), что функция f
(x)
= 3 x
– 2 в точке x
= 1
имеет предел равный 1, т.е.
![]() .
.
Решение:
Имеем для любого
![]()
0:
0:
![]() =
=![]() =
=![]()
![]() ,
отсюда получаем
,
отсюда получаем![]()
![]() ,
так что, если взять
,
так что, если взять![]() ,
то из того, что
,
то из того, что![]()
![]() будет следовать, что
будет следовать, что![]()
![]() .
.
4. Найти пределы:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Решение:
а)
На основании непрерывности функции в
точке
![]() искомый предел равен значению функции
в этой точке, т.е.
искомый предел равен значению функции
в этой точке, т.е.
![]()
б)
При
![]() числитель стремится к 20, т.е. является
ограниченной функцией, а знаменатель
стремится к 0, т.е. является бесконечно
малой величиной. Очевидно, что их
отношение есть величина бесконечно
большая, т.е.
числитель стремится к 20, т.е. является
ограниченной функцией, а знаменатель
стремится к 0, т.е. является бесконечно
малой величиной. Очевидно, что их
отношение есть величина бесконечно
большая, т.е.
![]() .
.
в)
![]() ,
так как отношение ограниченной функции
,
так как отношение ограниченной функции![]() к бесконечно большой величине
к бесконечно большой величине![]() есть величина бесконечно малая.
есть величина бесконечно малая.
5. Найти пределы:
а)
 ;
б)
;
б) .
.
Решение:
а)
Здесь
при
![]() числитель и знаменатель дроби стремятся
к нулю. В таком случае говорят, что имеет
место неопределенность
числитель и знаменатель дроби стремятся
к нулю. В таком случае говорят, что имеет
место неопределенность![]() .
Для того, чтобы избавится от неопределенности,
раскладываем
числитель и знаменатель на множители
и сокращаем дробь на одинаковый множитель
.
Для того, чтобы избавится от неопределенности,
раскладываем
числитель и знаменатель на множители
и сокращаем дробь на одинаковый множитель
![]() :
:

 .
.
б)
Здесь снова имеем неопределенность
![]() .
Для ее раскрытия умножим числитель и
знаменатель на выражение, сопряженное
числителю, получим
.
Для ее раскрытия умножим числитель и
знаменатель на выражение, сопряженное
числителю, получим


6. Найти:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)
 .
.
Решение:
а)
Числитель
и знаменатель дроби неограниченно
возрастают при
![]() .
В таком случае говорят, что имеет место
неопределенность вида
.
В таком случае говорят, что имеет место
неопределенность вида
![]() .
Вынесем
в числителе и знаменателе дроби х
в максимальной степени за скобки и
сократим, получим
.
Вынесем
в числителе и знаменателе дроби х
в максимальной степени за скобки и
сократим, получим
![]()
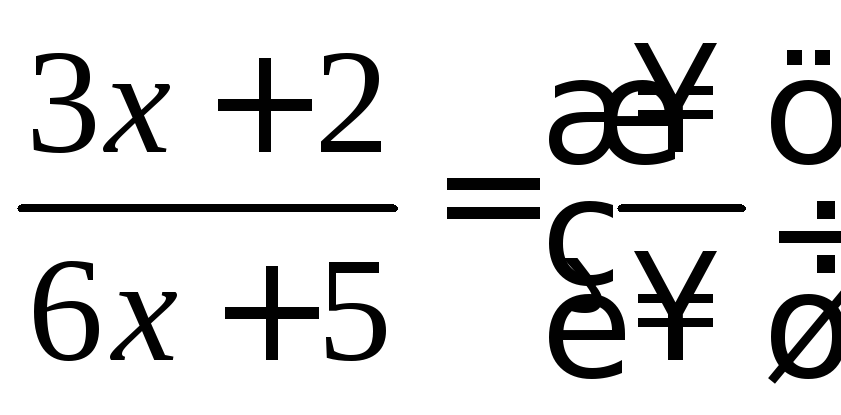 =
= .
.
б)
Имеем неопределенность вида
![]() .
Умножим и разделим выражение в скобках
на сопряженное ему выражение, получим
.
Умножим и разделим выражение в скобках
на сопряженное ему выражение, получим


в) Приведем дроби к общему знаменателю:
 =
=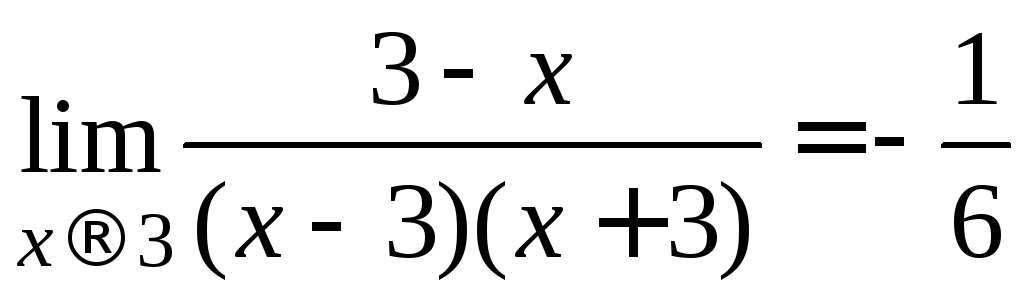 .
.
