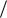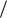учтем, что прогиб должен быть ограничен при
любых s. Однако первые 2 слагаемых не ограничены, т.к. |
|
e s при |
s . |
|
Отсюда вытекает, что должно быть |
С1 С2 0 . |
|
Хотя для анализа решения можно и не искать С3, С4, найдем их для |
иллюстрации того, как находится выражение для прогиба. |
|
В силу симметричности задачи под силой должно быть |
vmax v(0) . По |
теореме Ферма имеем соотношение: |
|
|
v (0) 0 .
Подставляя сюда (16.22) получаем:
v e s C3 sin s C4 cos s  s 0 e s C3 cos s C4 sin s
s 0 e s C3 cos s C4 sin s  s 0 0 . (16.23)
s 0 0 . (16.23)
Следующее уравнение относительно
соображений. Виду |
симметричности задачи |
рис 16.18) известна: |
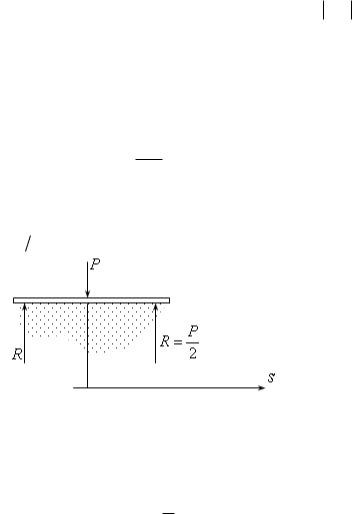
R P 2 . |
C3 |
получим из статических |
реакция основания справа (см.
Рис.16.18
Как видно из рис.16.18, в сечении под силой (при s = 0) согласно определению поперечной силы:
Из уравнения (16.18) получим:
|
|
|
|
M x |
|
|
|
|
|
|
3 |
v |
|
3 |
|
|
s |
|
|
Qy |
|
EJx |
|
|
|
|
|
cos( s) . |
|
|
s |
|
s |
3 |
4 C3e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя s = 0 находим из (16.24): |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3 |
C3 P / 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда: |
|
|
|
|
|
|
C3 |
C4 |
P / 8 |
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e s sin s e s cos s . |
v |
|
q |
, v |
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
част |
|
|
k |
одн |
|
|
8 3EJx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vmax
Анализ решения.
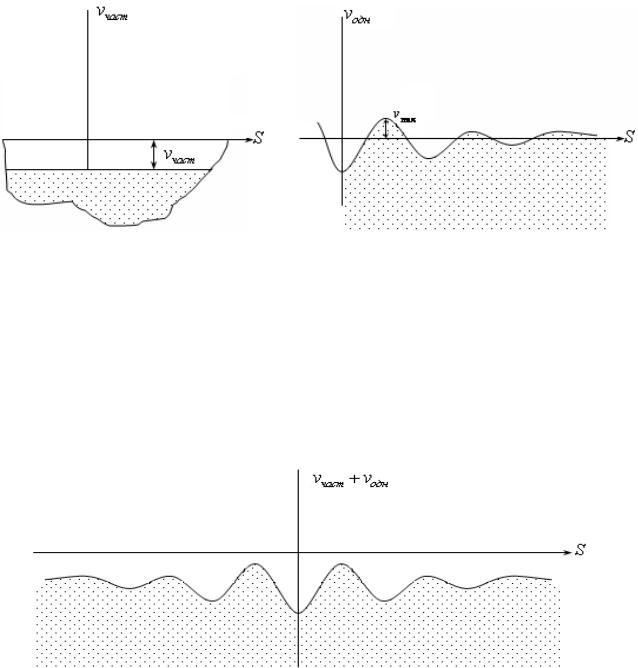
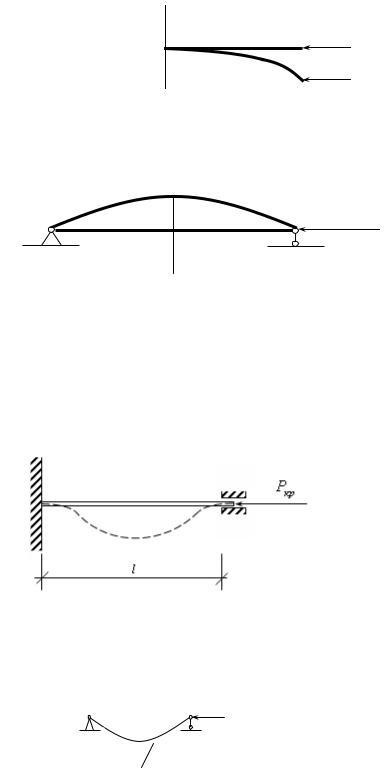
Изобразим графически полученные решения. Если нет силы Р, то согласно решению балка оседает как жесткое тело на величину vчаст (см.рис. 16.19).
Рис.16.19 |
Рис.16.20 |
Если есть только сила |
P , то осадка имеет волнообразный, но |
затухающий характер, как это изображено на рис. 16.20. Видно, что при отсутствии силы веса под действием только силы Р некоторые области балки приподнимаются над нулевым уровнем грунта.
Балка не будет приподниматься над первоначальным уровнем (т.е. будет отрицательным) только тогда, когда:
 vчаст
vчаст 
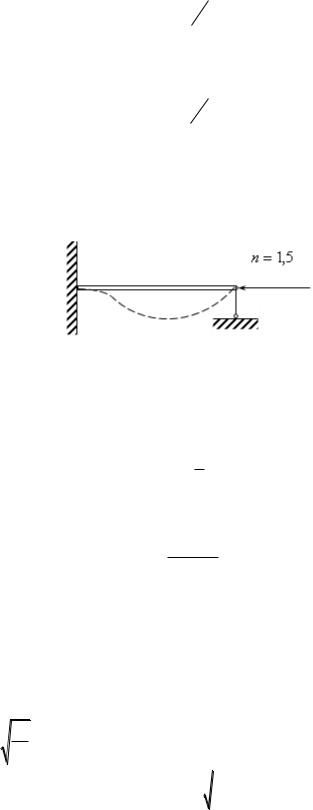
Суммарная осадка балки для этого случая изображена на рис.16.21.
Рис.16.21
Практические выводы из решения. Для того чтобы фундамент или дорожное полотно, не отрывались от грунта под действием сосредоточенной
силы необходимо, чтобы погонный вес фундамента или полотна был достаточно большой. Это означает, что толщина фундамента или дорожного полотна должна быть достаточно велика.
Рассмотрим сжатый стержень.
P
Рис.17.1
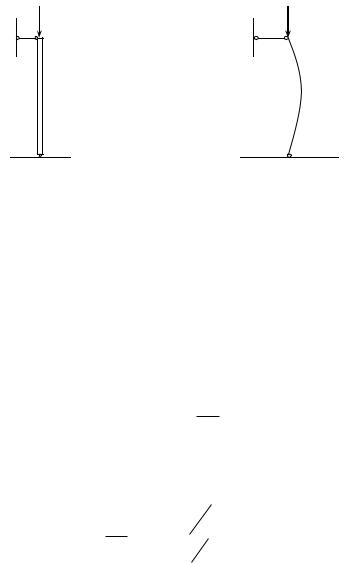
Пусть сила Р приложена в центре тяжести сечения стержня. На первый взгляд у силы Р нет плеча, значит M x 0 , значит, для изгиба нет причин.
Это справедливо при малых Р. Однако при некотором значении Р происходит резкая смена прямолинейной формы в криволинейную при малейшем поперечном воздействии (см.рис.17.2).
Это явление называется потерей устойчивости.
Сила Р, при которой это происходит, называется критической, а соответствующее ей напряжение называют критическим напряжением:
Опыт показывает, что для потери устойчивости стержня требуется меньшая сила, чем для разрушения сжатием, например, кубика из того же материала. Таким образом:
здесь Р* - разрушающая сила, σ* - предел прочности на сжатие.
Уменьшая критическое напряжение σкр на коэффициент запаса kуст получают допустимое напряжение [σ]уст , больше которого не должно быть рабочее напряжение:
|σ| ≤[σ]уст.
Для удобства расчетов часто пользуются таблицами, в которых приводится коэффициент υ, показывающий, насколько [σ]уст меньше основного допустимого напряжения [σ]:
υ=[σ]уст / [σ].
Если на растяжение и сжатие разрушающие напряжения различны, то под υ понимают величину:
υ=[σ]уст / [σ]сж.
Впервые формулу для вычисления Pкр |
вывел Л. Эйлер. |
Рис.17.3
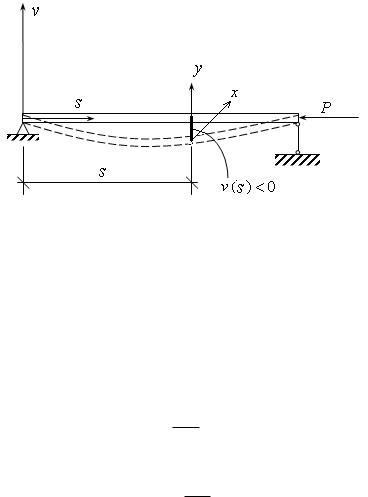
Рассмотрим балку, потерявшую устойчивость, т.е. |
P Pкр |
Изгиб здесь имеет место под действием момента
прогиб. Для отыскания |
Pкр |
используем уравнение изогнутой оси балки: |
|
|
|
EJxv M X |
Pкр v |
(17.1) |
Деля на EJ x находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
v |
|
кр |
v . |
|
|
|
|
|
|
|
|
|
EJ |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получили дифференциальное уравнение для |
v |
. Обозначим |
|
|
|
Тогда
Решение этого уравнения можно записать в виде:
v B Sin as C Cos as
Действительно, легко проверить, что после подстановки (17.3) в (17.2) слева получиться то же самое, что и справа.
Константы В и С отыскиваем из условий закрепления: (1): s 0, v 0 на левом краю
(2): s l, v 0 на правом краю
Sin 0 C Cos 0
Sin al C Cos al
на левом краю на правом краю
Отсюда |
|
|
|
(1): |
C 0 |
|
|
(2): |
или |
B 0, |
или |
Sin al 0 |
При |
B 0 : |
v 0 , значит |
прогиба нет, |
Поскольку |
это противоречит |
исходному |
уравнение |
|
|
|
|
|
Sin al 0 |
Оно имеет следующие решения:
т.е. нет потери устойчивости. предположению, то рассмотрим
.
1) al 0, |
2 ) al , |
3 ) al 2 ...... , |
(17.4) |
|
|
|
|
|
|
|
|
где |
a |
Pкр |
. |
|
|
|
|
|
|
|
|
EJ x |
|
|
Рассмотрим решения (17.4).
- это решение не подходит, т.к. стержень
не изогнется без нагрузки.
2) |
P |
|
l ; |
|
Pкр |
|
2 |
EJ |
|
. |
|
|
|
|
кр |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
EJ |
x |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
4 EJ |
|
|
3) |
|
l 2 ; |
|
|
Pкр |
2 |
|
. |
|
|
|
|
|
|
2 |
|
|
|
кр |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ |
x |
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Второе решение дает: |
v |
B Sin |
|
s |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Третье решение дает: |
v B Sin |
2 |
s |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(см. рис. 17.4)
(см. рис. 17.5)
Рис. 17.4 |
|
|
Рис. 17.5 |
Ясно, что при Pкр |
2 EJ |
x |
уже произойдет изгиб, и дальнейшее |
|
|
|
|
|
l |
|
|
повышение нагрузки невозможно, т.е. до величины
увеличиться не может. Аналогично и для других образом, получим что:
Pкр |
|
2 |
4 EJ |
|
нагрузка Р |
|
|
|
2 |
x |
|
|
|
|
|
|
|
|
|
l |
|
|
|
решений (17.4). Таким
Мы рассмотрели изгиб в плоскости листа, аналогично можно рассмотреть изгиб из листа, тогда получим:
|
|
|
2 EJ |
y |
. |
(17.7) |
кр |
|
Al |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, что изгиб произойдет в той плоскости, которая требует |
меньшее значение кр . Видно, что кр |
в (17.6) и (17.7) отличаются только |
моментом инерции. Таким образом, нужно взять тот случай, в котором момент инерции меньше:
Известно, что момент инерции достигает наименьшего значения относительно одной из главных центральных осей. Следовательно, для
вычисления |
кр |
необходимо найти главные центральные оси и главные |
моменты, а затем выбрать из них наименьшее.
Отметим особенности применения формулы (17.8)
1)Здесь предполагалось, что в обеих плоскостях опоры - шарнирные.
2)При выводе формулы предполагалось, что стержень упругий и
соблюдается закон Гука, поскольку уравнение изогнутой оси балки получено при условии, что стержень линейно упругий. Следовательно, формула верна только тогда, когда справедлив закон Гука.
Рис. 17.6
Таким образом, формула Эйлера справедлива только тогда, когда:
Примечание. Вывод формулы Эйлера можно провести соображений, а именно из закона сохранения энергии, полагая что W
(17.9)
и из другихЭ , где
|
|
1 |
|
|
1 |
|
|
|
M |
x |
|
|
1 |
|
|
M |
x |
|
|
|
Э |
|
|
dV |
|
|
|
|
|
y |
|
|
|
|
|
y dV , |
W |
|
2 V |
2 |
Jx |
E |
Jx |
|
|
|
|
|
|
|
|
|
|
|
где - перемещение точки приложения силы вдоль оси стержня.
17.2 Другие условия закрепления
Рассмотрим случай консольной балки:
l
Рис. 17.7
Будем пользоваться геометрической аналогией. Эта задача аналогична
приведенной ниже: 2l
Pкр
Рис. 17.8
Правая еѐ половина точно такая же, как балка, рассматриваемая на рис.17.7, следовательно:
Рассмотрим теперь случай защемления с двух концов:
Рис. 17.9
Здесь только половина балки (еѐ средняя часть) изгибается как шарнирная (см. рис.17.10):
l 2
Рис. 17.10
117
Введем параметр n – число волн, которые образуются при продольном изгибе балки, тогда получим:
Пользуясь этой аналогией, получим еще одну (приближенную) формулу для случая, изображенного на рис. 17.11:
Рис. 17.11
Врасчетной практике вместо n используют - коэффициент
Запишем формулу Эйлера с помощью нового обозначения:
|
|
|
|
|
|
|
|
|
2 |
EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
min |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кр |
|
(l) |
2 |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кроме того, в теории устойчивости вводят параметр: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
( l)2 |
A |
|
. |
|
|
|
|
|
|
|
|
|
|
|
Jmin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь |
|
- |
|
безразмерная |
величина, являющаяся |
длиной, называется гибкостью. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Для корня |
|
A |
вводят специальное обозначение: |
|
J |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ix |
|
|
|
J x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
Аналогично,
(17.10)
(17.11)
относительной
(17.12)
|
|
|
|
iy |
|
|
J |
y |
. |
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
Величины ix , iy |
- называются радиусами инерции сечения. |
В новых обозначениях получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
2 |
E |
|
|
|
|
|
|
|
|
|
. |
|
|
|
кр |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это наиболее употребительный вид формулы Эйлера.
17.3 Предельная гибкость. Длинный стержень
Рассмотрим условие применимости формулы Эйлера (17.9):
кр пц .
Подставим сюда (17.14):
Отсюда:
Обозначим правую часть через:
Таким образом, формула Эйлера применима, если:
*
То есть, если условная длина достаточно большая, то формула Эйлера применима. Поэтому такие стержни называют длинными.
17.4 Формула Ясинского
Он изучил более 2000 экспериментов и показал, что если можно вычислять по формуле:
y с
Это и есть формула Ясинского.
Здесь a и b константы материала. Например, для стали:
a2,66 T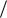 см2 26, 6 kH
см2 26, 6 kH см2
см2
b0,0066 T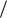 см2 0,066 kH
см2 0,066 kH см2
см2
Кроме того, для стали предел текучести
T |
2,4T см |
2 |
24 kH см |
2 |
. |
|
|
Из формулы Ясинского видно, что если |
очень мал, то |
|
кр 2,66T см2 T . |
|
|
Это означает, что для изгиба стержня-образца требуется больше усилий, чем для того, чтобы сплющить этот образец. Поэтому формула Ясинского справедлива только тогда, когда:
Это условие применимости формулы Ясинского.
то этот стержень называют стержнем средней
, то стержень называют коротким:
17.5 Продольный изгиб
Снова рассмотрим изгиб балки под действием продольной центральной силы Р, но предварительно изогнутой приложенными по концам сосредоточенными моментами m (см. рис. 17.12). Этот момент может быть вызван внецентренным нагружением продольной силой Р, если он имеет эксцентриситет е. Тогда m=Ре.