
15
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
_______________________________________________________________
КАЗАНСКАЯ ГОСУДАРСТВЕННАЯ АРХИТЕКТУРНО-СТРОИТЕЛЬНАЯ АКАДЕМИЯ
Кафедра физики
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ ПО ФИЗИКЕ
для студентов специальностей
290300, 290600, 290700, 290800, 291000, 291400, 291500
Часть 1.Механика и молекулярная физика Лабораторная работа № 15
Изучение деформации деревянного бруса
Казань
2003
Составитель: В. В. Алексеев
Под редакцией Л. И. Маклакова
УДК 531.781
Методические указания к лабораторным работам по физике для студентов спе-
циальностей 290300, 290600, 290700, 290800, 291000, 291400, 291500
Лабораторная работа № 15. ²Изучение деформации деревянного бруса."/ Казанская государственная архитектурно-строительная академия. Составитель В. В. Алексеев (под редакцией Л. И. Маклакова,). Казань, г.
В методических указаниях изложены вопросы, связанные с механическими свойствами твердого тела. Показана качественная связь механических свойств с атомным строением тел. Описывается экспериментальная установка, позво- ляющая изучать прогиб балок, изготовленных из различных материалов.
Стр. 15. Илл. 6. Табл.2.
Рецензент: доцент кафедры молекулярной физики Казанского госуниверси- тета Г. Г. Пименов
ÓКазанская государственная архитектурно-
строительная академия, |
г. |
2

Введение
При строительстве и конструировании различных сооружений, в том чис- ле и строительных, необходимо знать механические свойства используемых ма- териалов: бетона, железобетона, стали, пластмасс и т.д. Сведения о механиче- ских свойствах различных материалов получают экспериментально, изучая де- формацию твердых тел.
Деформацией называется изменение формы и размеров тела под дейст-
вием приложенных сил. Различают два вида деформации — упругую и пласти-
ческую. Упругой называется деформация, исчезающая после прекращения дей- ствия приложенных сил. Деформация, не исчезающая после снятия сил, назы-
вается пластической. Вид деформации зависит от материала тела и от величи- ны приложенного усилия. Усилием называется внешняя сила, отнесённая к единице площади, т.е.
Р = |
dF |
, |
(1) |
|
dS |
||||
|
|
|
где dF — сила, действующая на бесконечно малую площадку dS. При деформа- ции в теле возникают силы, противодействующие внешним силам. Их называют упругими силами. Упругая сила, отнесенная к единице площади, называется
напряжением:
σ = |
dFупр |
(2) |
dS |
где dFупр — упругая сила, действующая на бесконечно малую площадку dS. В общем случае напряжение составляет некоторый угол с площадкой. Поэтому его можно разложить на две составляющие: σn, перпендикулярную к площадке, и στ касательную к ней (рис. 1). Их соответственно называют нормальным и ка- сательным напряжением.
Деформацию тел оценивают абсолютной и относительной деформацией.
Абсолютной деформацией x называют разность конечного x и начального x0 размера тела, т.е.
x = x – x0 |
(3 |
3
σn
στ σ
Рис. 1
Абсолютная деформация при растяжении положительная, а при сжатии — от- рицательная. Относительной деформацией ε называется отношение абсолют- ной деформации к первоначальному размеру тела, т.е.
ε = x / x0 |
(4) |
Относительная деформация показывает, на какую часть изменились пер- воначальные размеры тела. Существуют различные виды деформации: про- дольное растяжение (или сжатие), сдвиг, кручение, изгиб. Рассмотрим некото- рые из них.
1. Продольное растяжение или сжатие.
Простейшим видом деформации твёрдого тела является продольное рас- тяжение (сжатие). Оно возникает в тонком стержне (рис. 2), один конец которо- го закреплён, а к другому вдоль его оси приложена сила F, равномерно распре- делённая по сечению. В результате этого длина стержня изменяется от l0 до l.
Тогда абсолютная и относительная деформация стержня, согласно (3) и (4), равны:
l = l – l0, ε = l /l0. |
(5) |
Предположим, что площадь поперечного сечения стержня одинакова по всей длине и равна S. Тогда, согласно (1), усилие, действующее на стержень,
будет равно
Р = |
F |
. |
(6) |
|
|||
|
S |
|
|
так как сила равномерно распределена по сечению. Эти усилия одинаковы в любом поперечном сечении стержня. Они вызывают появление внутри стержня напряжений, которые будут также одинаковы вдоль всей длины стержня. При упругой деформации напряжение равно усилию, но направлено в противопо- ложную сторону, т.е.
4
|
0 |
0 |
r |
l |
l |
l |
l |
F |
|
|
r |
|
|
|
|
F |
|
|
|
|
|
Рис.2. |
|
|
σ = Р = |
F |
. |
(6 а) |
|
|||
|
S |
|
|
Опытным путем английский физик Р. Гук установил закон, названный его именем: в пределах упругости относительная деформация пропорциональна усилию, приложенному к телу, т.е.
ε = |
Р |
. |
(7) |
|
|||
|
Е |
|
|
или напряжение упруго деформированного тела пропорционально его относительной деформации:
σ = Е × e, |
(7 а) |
где Е — модуль Юнга, зависящий от свойств материала, из которого изготовле- но тело.
Выясним физический смысл модули Юнга. Из формулы (7) следует, что если ε = 1, т.е. когда l = l0 (см. (5)), то Е = Р, т.е. модуль Юнга равен усилию, которое надо приложить к телу, чтобы изменить его длину вдвое при сохра-
нении упругой деформации. В действительности же подавляющее число мате- риалов разрушается значительно раньше, чем это произойдёт.
Наряду с продольной деформацией стержня наблюдается и изменение его поперечных размеров. Причём при растяжении поперечные размеры стержня уменьшаются, а при сжатии — увеличиваются. Пусть b0 — толщина стержня до деформации, b — после деформации. За толщину для круглого стержня прини- мают его диаметр, для прямоугольного стержня — одну из сторон его прямо- угольного основания и т.д. Тогда относительная поперечная деформация εn бу-
дет равна εn = b /b0, где b =b – b0.
Как следует из опытов, относительное изменение поперечных размеров стержня пропорционально тому же усилию, приложенному стержню. Поэтому оно пропорционально и величине относительного изменения длины стержня.
5
Отношение относительной поперечной деформации к соответствующей относи-
тельной продольной деформации называется коэффициентом Пуассона
μ = |
ε n |
= |
b / b0 . |
|
ε |
||||
|
|
l / l0 |
Коэффициент Пуассона зависит только от материала. Его значение находится в ин- тервале от 0 до 0.5. Для пористых материалов (например, пенопластов) μ = 0, так как при деформации тел из таких материалов их поперечные размеры не изменя- ются, для резины и других высокоэластичных материалов он близок к 0.5.
Таким образом, упругие свойства изотропного твёрдого тела характери- зуются модулем Юнга и коэффициентом Пуассона. Все другие упругие посто- янные, применяемые для описания других видов деформации, могут быть вы- ражены через них.
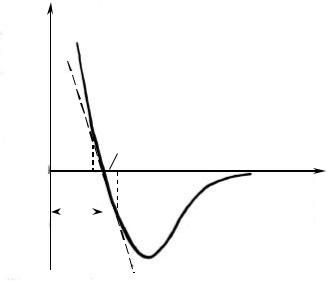
Детальное изучение деформаций. Возникающих в твёрдых телах под дей- ствием внешних сил, требует учёта их внутренней структуры. Твёрдые тела имеют кристаллическое строение, т.е. частицы (атомы, ионы), составляющие тело, расположены в определённом порядке. Каждая частица испытывает воз- действия со стороны соседних частиц. Общий вид зависимости силы f взаимо- действия частиц от расстояния r между ними приведён на рис. 3. Значения f <0 соответствуют силам притяжения, а значения f > 0 — силам отталкивания. При некотором расстоянии r0 силы притяжения и отталкивания уравновешивают друг друга и равнодействующая сила взаимодействия равна нулю. Расстояние r0 соответствует расстоянию между положениями равновесия частиц. Тепловое движение частиц будет проявляться в виде малых колебаний частиц около сво- их положений равновесия. В отсутствии внешних сил частицы в твёрдом теле
|
|
|
|
|
располагаются на расстояниях r0 |
|||
f |
|
|
|
друг от друга. |
|
|
||
|
|
|
|
|
Рассмотрим продольное |
рас- |
||
|
|
|
|
|
тяжение (или сжатие) стержня дли- |
|||
|
|
|
|
|
ной l0 и площадью поперечного се- |
|||
|
|
|
|
|
чения S под действием силы F, рав- |
|||
|
|
|
r |
|
номерно распределённой по сече- |
|||
0 |
|
|
|
нию (рис.2). Пусть длина стержня |
||||
r0 |
|
f |
r |
изменилась на некоторую величину |
||||
|
||||||||
|
|
l. При этом расстояния между со- |
||||||
|
|
|
|
|
||||
|
|
|
|
|
седними |
частицами |
вдоль |
оси |
|
|
|
|
|
||||
|
|
|
|
|
стержня |
изменяется на |
некоторую |
|
|
|
|
Рис. 3 |
|
величину r. Очевидно, |
что относи- |
||
|
|
|
|
тельная деформация стержня будет |
||||
равна относительному изменению расстояния между атомами, т. е.
l = r . l0 r0
6

Отсюда |
Dr = |
r0 |
Dl. |
(8) |
|
l0 |
|||||
|
|
|
|
При смещении частиц из своих положений равновесия между ними воз- никают силы притяжения Df при растяжении стержня или отталкивания при его сжатии, причем |Df| возрастает с увеличением Dr. Эти силы называются упруги- ми. При малых деформациях, пока Dr << Dr0 (а следовательно и Dl << Dl0), кри- волинейную зависимость Df от Dr можно практически заменить прямой линией (пунктир на рис. 3). Тогда Df будет пропорциональна Dr
Df = –k Dr |
(9) |
где k — коэффициент пропорциональности, зависящий от конкретного вида кривой взаимодействия для частиц данного твёрдого тела. Знак "–" отражает тот факт, что направление силы Df противоположно направлению внешней силы F.
Рассматриваемый стержень можно считать состоящим из ряда параллель- ных цепочек частиц. Обозначим через n0 число этих цепочек, приходящихся на единицу поперечного сечения стержня. Тогда во всем поперечном сечении бу- дет действовать суммарная сила притяжения (или отталкивания):
S Df = – N×Df = – k Dr n0 S, |
(10) |
где N = n0S — число цепочек частиц на всем поперечном сечении S.
Величина Dr будет возрастать до тех пор, пока эта сила не уравновесит внеш- нюю силу F, т.е. F = S Df. Отсюда, учитывая (8), получаем:
F = k Dr n0S = k n0 r0 S Dl / l0. |
(11) |
Обозначим k n0 r0 = E. Тогда из (11) следует, что
l = 1 × F . l0 E S
Но Dl /l0 = e — относительная деформация и F/S = P — усилие.
Итак |
ε = |
Р |
. |
(12) |
|
||||
|
|
E |
|
|
т.е. получен закон Гука.
Наиболее удобным способом исследования механических свойств твёрдого тела являются испытания тела на растяжение и построение диаграмм растяжения, т.е. зависимости между относительным удлинением e = Dl/l0 и усилием P.
7
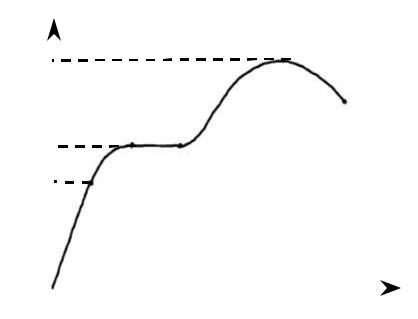
Типичная кривая такой зависимости приведена на рис.4. Пока относи- тельное удлинение мало имеется пропорциональность между ε и Р, т.е. справед-
Р
Рпр |
|
C |
|
|
|||
|
|
|
|
Рт |
|
Д |
|
|
В В' |
||
Рп |
|
||
|
А |
||
0 |
|
ε |
|
|
|
|
|
Рис.4
лив закон Гука. Наибольшее усилие Рп, до которого еще выполняется закон Гу-
ка, называется пределом пропорциональности. Дальнейшее увеличение уси- лия приводит к более быстрому возрастанию относительного удлинения. При усилии Рт, называемого пределом текучести, относительная деформация про- должает возрастать без увеличения усилия (горизонтальная прямая ВВ′). Ино- гда этот участок отсутствует. Затем для продолжения деформации необходимо снова увеличивать усилие. Возрастание усилия происходит до тех пор, пока на образце не появится местное сужение. Это усилие Рпр называется пределом прочности. Далее образец удлиняется даже при уменьшающемся усилии и, на- конец, разрывается (точка Д).
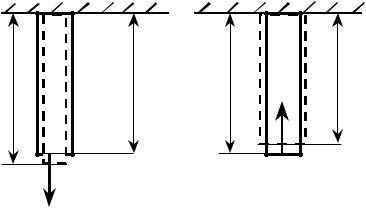
2. Изгиб. Рассмотрим однородный прямолинейный брус с одинаковым по всей длине прямоугольным поперечным сечением, лежащим на двух опорах. Выделим в нём средний слой, называемый нейтральным. Проведём вертикаль- ное продольное сечение А1А2В1В2 бруса (рис. 5а). Пусть длина бруса равна l0.
Линия N1N2 называется нейтральной линией. Под действием силы F, при- ложенной к середине бруса, возникает деформация изгиба. В результате этого прямые А1А2, N1N2, В1В2 и все прямые, параллельные им, превращаются в дуги концентрических окружностей с центром в точке 0 (рис.5 б). При этом длина линии N1N2 не меняется. Волокна же, лежащие ниже этой линии, растягивают- ся, а лежащие выше укорачиваются. Таким образом, продольные слои, распо- ложенные со стороны выпуклости от нейтрального слоя, растянуты, а слои, расположенные по другую сторону от него — сжаты. Пусть R — радиус ней- тральной линии N1N2. Тогда l0 = αR, где α — центральный угол, опирающийся на дугу N1N2 (угол надо измерять в радианах). Рассмотрим волокно бруса, находящее- ся на расстоянии ξ от нейтральной линии. Величина ξ положительна, если волок- но находится ниже нейтральной линии, а отрицательна, если оно находится выше.
8
|
|
l0 |
|
R |
||
A1 |
|
N2 A2 |
A1 |
|||
N1 |
|
N1 |
||||
B1 |
|
B2 |
B1 |
|||
|
|
|
|
|||
|
а |
|
|
|
F |
|
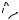
 α
α
λ  l0/2
l0/2  A2
A2
 N2
N2
 B2
B2
б
Рис. 5
Очевидно, что длина рассматриваемого волокна будет l0 = α(R + ξ), а удлинение l = ( R+ ξ) α – Rα.
|
Согласно закону Гука, напряжение, действующее вдоль рассматриваемо- |
|||||||
го волокна, равно |
l |
|
αξ |
|
|
|||
|
|
|
σ = Е × ε = Е × |
= E × |
. |
|
||
|
|
|
|
|
||||
|
|
|
|
l0 |
l0 |
|
||
Но |
α = |
1 |
. Тогда |
|
σ = |
Е × ξ. |
(13) |
|
|
|
|||||||
|
l0 |
R |
|
|
R |
|
||
Итак, напряжение пропорционально расстоянию от нейтрального слоя. За меру деформации при изгибе принимается стрела прогиба, т.е. рас-
стояние, на которое опускается точка приложения силы, действующей на брус
(рис. 5 б).
Можно показать, что для бруса с прямоугольным сечением при малых деформациях, т.е. когда справедлив закон Гука, стрела прогиба равна
λ = Fl03 4ab3 E
где F — сила, приложенная в середине бруса, l0 — начальная длина, a — шири- на, b — высота бруса (толщина), Е — модуль Юнга. Эта формула может быть
использована для расчёта модуля Юнга
E = |
Fl0 |
3 |
. |
(14) |
|
|
|||
|
4ab3λ |
|
||
Цель работы
Ознакомиться с механическими свойствами твердого тела, определить модуль Юнга исследуемого материала и распределение напряжений по попе- речному сечению бруса.
9
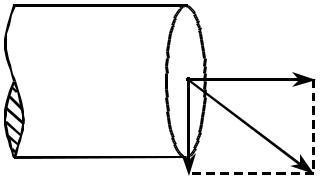
Описание установки
Исследуемый брус (1) лежит на двух опорах (2), расстояние между кото- рыми равно l0 (рис.6). Опоры крепятся к массивному основанию (3). Над иссле- дуемым брусом посредине расположен микровинт с рукояткой (4). Вращением этой рукоятки по часовой стрелке осуществляется прогиб бруса. Стрела проги- ба λ измеряется индикатором (5) (отсчёты проводятся по чёрной шкале), а дей- ствующая сила F механическим динамометром (6), расположенными под бру- сом. Относительная деформация различных слоёв бруса определяется измери- телем деформации ИДЦ-1. Датчиками являются тензорезисторы (7), сопротив-
ление которых зависит от степени их деформа- |
|
Таблица 1 |
|
ции. Они наклеены на боковую грань бруса. Рас- |
|
||
№ датчика |
ξ , мм |
||
стояние ξ от датчиков до нейтрального слоя ука- |
|||
1 |
-20,4 |
||
заны в табл. 1. Знак «–» означает, что тензорези- |
|||
2 |
-9,6 |
||
сторы находятся выше нейтрального слоя, а «+» |
|||
3 |
+1,6 |
||
— ниже. К измерителю деформации подключает- |
|||
4 |
+10 |
||
ся магазин сопротивлений. Питание прибора |
|||
5 |
+20 |
||
осуществляется от сети напряжением 220 В через |
|||
|
|
||
понижающий трансформатор. |
|
|
Порядок выполнения работы
1.Включите установку в сеть
2.Установите на магазине сопротивлений сопротивление 400 — 405 Ом.
3.Поставьте переключатель каналов на измерителе деформации в поло- жение 1.
4.Проведите измерения при ненагруженном брусе на каналах 1 — 5 пу- тём кратковременного нажатия кнопки «ПУСК» и переключения кана- лов. После каждого нажатия зажигается цифровое табло. Переключение каналов производить после погасания табло. Показания табло заносите в таблицу 2.
Таблица 2
№ канала |
ξ, мм |
O, H |
F, H |
ε |
σ, 105 |
Па |
|
|
n1 |
n2 |
|
|
|
|
|
|
|
|
||
1 |
–20,4 |
|
|
|
|
|
2 |
–9,4 |
|
|
|
|
|
3 |
+1,6 |
|
|
|
|
|
4 |
+10 |
|
|
|
|
|
5 |
+20 |
|
|
|
|
|
5. Поворотом рукоятки (4) по часовой стрелке (см. рис. 6) осуществите прогиб бруса. Сила F = 200 Н соответствует стрела прогиба λ=0,55 мм, 400 Н —
1,10 мм, 600 Н — 1,65 мм.
10
