Ток смещения

Как указывалось, Максвелл высказал гипотезу, что переменное магнитное поле создаёт вихревое электрическое поле. Он сделал и обратное предположение: переменное электрическое поле должно вызывать возникновение магнитного поля. В дальнейшем эти обе гипотезы получили экспериментальное подтверждение в опытах Герца. Появление магнитного поля при изменении электрического поля можно трактовать так, как будто бы в пространстве возникает электрический ток. Этот ток был назван Максвеллом током смещения. Ток смещения в отличие от тока проводимости в металлах не связан с движением электрических зарядов, а обусловлен переменным электрическим полем. В действительности никакого тока нет, а есть лишь изменяющееся со временем электрическое поле, которое и создаёт магнитное поле. Однако использование этого термина удобно.

Выясним, от чего зависит ток смещения на простом примере. Рассмотрим плоский конденсатор, на обкладках которого имеются заряды q противоположного знака, равномерно распределённые по обкладкам с поверхностной плотностью, равной = q/S, где S — площадь обкладки. Внутри конденсатора возникает электрическое поле. Напряжённость этого поля равна

. (11)

Рис. 2

Замкнём обкладки конденсатора проводником (рис. 2). Это приводит к возникновению тока проводимости в проводнике, приводящего к уменьшению заряда на обкладках конденсатора, следовательно, и к ослаблению электрического поля внутри конденсатора. Изменение электрического поля вызывает появление магнитного поля между пластинами конденсатора, обусловленного как бы током смещения силой I_cм, текущего внутри конденсатора. Сила этого тока должна равняться силе тока проводимости I_пр, поскольку электрическая цепь не имеет разветвлений. Поэтому I_cм = I_пр. Силу тока проводимости находим по формуле Подставляя в это выражениеq, найденное из (11), и вынося постоянные за знак производной, получаем силу тока смещения: Плотность тока смещения будет равна

(12)

В общем случае напряжённость электрического поля может зависеть от координат и времени. Поэтому в выражении (36.2) производную надо заменить частной производной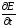. Тогда

(13)

и сила тока смещения через площадку S, перпендикулярную к направлению этого тока, равна

. (14)

Ток смещения может возникать не только в вакууме или диэлектрике, но и в проводниках, по которым течёт переменный ток. Однако в этом случае он пренебрежимо мал по сравнению с током проводимости.

Максвелл ввёл понятие полного тока. Сила I полного тока равна сумме сил I_пр и I_см токов проводимости и смещения, т.е. I = I_пр + I_см. Используя (14), получаем:

(15)

где S  площадь поперечного сечения проводника.

Уравнения максвелла

Введение двух гипотез о существовании вихревого электрического поля и тока смещения позволили Максвеллу создать единую теорию электромагнетизма. В основе этой теории находятся четыре уравнения, названные уравнениями Максвелла, которые играют в учении об электромагнетизме такую же роль, как законы Ньютона в классической механике. Рассмотрим эти уравнения.

1. Первое уравнение. Согласно (10), циркуляция напряжённости вихревого электрического поля равна

(16)

Но Тогдагде (— проекция производной по времени индукции магнитного поля на направление нормалик площади контура. Поскольку в общем случае индукция магнитного поля зависит от координат и времени, тонадо заменить частной производной. С учётом этого уравнение (16) запишется

(17)

Из этого уравнения следует, что источником электрического поля является изменяющееся со временем магнитное поле.

2. Второе уравнение. Максвелл обобщил закон полного тока, введя в её правую часть полный ток , гдеS  площадь замкнутого контура длиною l. Учитывая это, закон полного тока запишется

(18)

поскольку Это уравнение показывает, что магнитное поле может создаваться как движущимися зарядами (электрическим током), так и переменным электрическим полем.

3. В качестве третьего и четвертого уравнений Максвелл взял теорему Гаусса для электростатического и магнитного полей

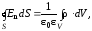(19) (20)

Соотношение (19) свидетельствует о том, что линии напряжённости электростатического поля начинаются и кончаются на электрических зарядах, а из (20) следует, что линии магнитной индукции всегда замкнуты, т.е. в природе не существует магнитных зарядов. Необходимо отметить, что нумерация уравнений Максвелла произвольная.

Из уравнений (17) и (18) вытекает, что переменное магнитное поле всегда связано с создаваемым им электрическим полем, и наоборот, переменное электрическое поле связано с создаваемым им магнитным полем. Таким образом, эти поля взаимосвязаны и образуют единое электромагнитное поле. Поэтому отдельное рассмотрение электрических и магнитных полей носит относительный характер. Так, например, если электрическое поле создаётся неподвижными зарядами в одной системе отсчёта, то относительно другой они могут двигаться и, следовательно, порождают одновременно и электрическое и магнитное поля. Уравнения Максвелла являются основой единой теории электрических и магнитных явлений.