Явление и закон самоиндукции

Явление возникновения э.д.с. в том же проводнике, по которому течёт переменный ток, называют самоиндукцией, а саму э.д.с.  э.д.с. самоиндукции. Возникновение э.д.с. самоиндукции объясняется следующим. Переменный ток, проходящий по проводнику, порождает вокруг себя переменное магнитное поле, которое, в свою очередь, создаёт магнитный поток, изменяющийся со временем, через площадь, ограниченную проводником.

Согласно явлению электромагнитной индукции, это изменение магнитного потока и приводит к появлению э.д.с. Значение э.д.с. самоиндукции найдём, подставляя выражение (1) в закон электромагнитной индукции (см. (14) лекцию №9) и полагая, что L = const: Итак,

(4)

Итак, э.д.с. самоиндукции в проводнике пропорциональна скорости изменения силы тока, текущего по нему.

Под действием э.д.с. самоиндукции создаётся индукционный ток, называемый током самоиндукции.

Энергия магнитного поля

Рис. 1

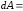
Пусть в электрической цепи (рис. 1) протекает постоянный ток силой I. Если отключить источник тока и замкнуть цепь (переключатель П перевести в положение 2), то в ней некоторое время будет течь убывающий ток, обусловленный э.д.с. самоиндукции _s, равной . Элементарная работа, совершаемая э.д.с. самоиндукции по переносу по цепи элементарного зарядаdq = I·dt, равна Сила тока изменяется от I до 0. Поэтому, интегрируя это выражение в указанных пределах, получаем работу, совершаемую э.д.с. самоиндукции за время, в течение которого происходит исчезновение магнитного поля: Совершение этой работы сопровождается нагреванием проводника и окружающей среды и исчезновением магнитного поля, которое первоначально существовало вокруг проводника. Поскольку никаких других изменений в окружающей среде не происходит, то можно заключить, что магнитное поле обладает энергией, за счёт которой и совершается работа. Итак, энергия магнитного поля, существующего вокруг проводников с током, равна

W_B = LI²/ 2. (5)

Выразим энергию магнитного поля через величины, характеризующие само поле. Проделаем это на примере соленоида. Из формул (2) и (3) I = B/(₀n) и L =₀ n²V. Подставляя эти выражения в (5), получаем, что

(6)

Магнитное поле внутри соленоида однородное (= const). Поэтому объёмная плотность энергииw_B магнитного поля, т.е. энергия единицы объёма поля, внутри соленоида равна

w_B = W_B/V = B² /(2₀). (7)

Эта формула справедлива и в случае неоднородных статических и переменных магнитных полей.

Электромагнитное поле вихревое электрическое поле

Из закона Фарадея для электромагнитной индукции

(8)

следует, что при всяком изменении магнитного потока, пронизывающего площадь, охватываемую проводником, в нём возникает э.д.с. индукции, под действием которой в проводнике появляется индукционный ток, если проводник замкнутый.

Для объяснения э.д.с. индукции Максвелл выдвинул гипотезу, что переменное магнитное поле создаёт в окружающем пространстве электрическое поле. Это поле действует на свободные заряды проводника, приводя их в упорядоченное движение, т.е. создавая индукционный ток. Таким образом, замкнутый проводящий контур является своеобразным индикатором, с помощью которого и обнаруживается данное электрическое поле. Обозначим напряжённость этого поля через . Тогда э.д.с. индукции

. (9)

(см. понятие э.д.с. источника). Объединяя соотношения (8) и (9), получаем

(10)

Из электростатики известно, что циркуляция напряжённости электростатического поля равна нулю, т.е.где— напряжённость электростатического поля. Это соотношение является условием потенциальности электростатического поля. Однако из (10) следует, что, т.е.электрическое поле, возбуждаемое изменяющимся со временем магнитным полем, является вихревым (не потенциальным).

Следует отметить, что линии напряжённости электростатического поля начинаются и заканчиваются на зарядах, создающих поле, а линии напряжённости вихревого электрического поля всегда замкнутые.