Магнитный поток.

По аналогии с потоком напряжённости электрического поля вводится поток индукции магнитного поля или магнитный поток. Магнитным потоком через некоторую поверхность называют число линий магнитной индукции, пронизывающих её. Пусть в неоднородном магнитном поле находится поверхность площадью S. Для нахождения магнитного потока через неё мысленно разделим поверхность на элементарные участки площадью dS, которые можно считать плоскими, а поле в их пределах однородным (рис. 4). Тогда элементарный магнитный поток dФ_B через эту поверхность равен: dФ_B = B·dS·cos  = B_n dS, где B — модуль индукции магнитного поля в месте расположения площадки, — угол между вектором 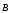и нормалью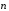к площадке,B_n = B·cos  — проекция индукции магнитного поля на направление нормали. Магнитный поток Ф_B через всю поверхность равен сумме этих потоков dФ_B, т.е.

Рис. 4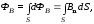

(6)

поскольку суммирование бесконечно малых величин — это интегрирование.

В системе единиц СИ магнитный поток измеряется в веберах (Вб). 1 Вб = 1 Тл·1 м².

Теорема гаусса для магнитного поля

В электродинамике доказывается следующая теорема: магнитный поток, пронизывающий произвольную замкнутую поверхность, равен нулю, т.е.

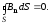(7)

Это соотношение получило название теоремы Гаусса для магнитного поля. Эта теорема является следствием того, что в природе не существует "магнитных зарядов" (в отличие от электрических) и линии магнитной индукции всегда замкнуты (в отличие от линий напряжённости электростатического поля, которые начинаются и заканчиваются на электрических зарядах).

Работа по перемещению проводника с током в магнитном поле

Рис. 5

Известно, что на проводник с током в магнитном поле действует сила Ампера. Если проводник перемещается, то при его движении эта сила совершает работу. Определим её для частного случая. Рассмотрим электрическую цепь, один из участков DC которой может скользить (без трения) по контактам. При этом цепь образует плоский контур. Этот контур находится в однородном магнитном поле с индукцией перпендикулярной к плоскости контура, направленном на нас (рис. 5). На участок DC действует сила Ампера,

F = BIl·sin =BIl, (8)

где l — длина участка, I — сила тока, текущего по проводнику. — угол между направлениями тока и магнитного поля. (В данном случае = 90 и sin  = 1). Направление силы находим по правилу левой руки. При перемещении участка DC на элементарное расстояние dx совершается элементарная работа dA, равная dA = F·dx. Учитывая (8), получаем:

dA = BIl·dx = IB·dS = I·dФ_B, (9)

поскольку dS = l·dx — площадь, описываемая проводником при своём движении, dФ_B=B·dS — магнитный поток через эту площадь или изменение магнитного потока через площадь плоского замкнутого контура. Выражение (9) справедливо и для неоднородного магнитного поля. Таким образом, работа по перемещению замкнутого контура с постоянным током в магнитном поле равна произведению силы тока на изменение магнитного потока через площадь этого контура.

Явление электромагнитной индукции

Явление электромагнитной индукции заключается в следующем: при всяком изменении магнитного потока, пронизывающего площадь, охватываемую проводящим контуром, в нём возникает электродвижущая сила. Её называют э.д.с. индукции. Если контур замкнут, то под действием э.д.с. появляется электрический ток, названный индукционным.

Рассмотрим один из опытов, проведённых Фарадеем, по обнаружению индукционного тока, следовательно, и э.д.с. индукции. Если в соленоид, замкнутый на очень чувствительный электроизмерительный прибор (гальванометр) (рис. 6), вдвигать или выдвигать магнит, то при движении магнита наблюдается отклонение стрелки гальванометра, свидетельствующее о возникновении индукционного тока. То же самое наблюдается при движении соленоида относительно магнита. Если же магнит и соленоид неподвижны относительно друг друга, то и индукционный ток не возникает. Таким образом, при взаимном движении указанных тел происходит изменение магнитного потока, создаваемого магнитным полем магнита, через витки соленоида, что и приводит к появлению индукционного тока, вызванного возникающей э.д.с. индукции.

Рис. 6

ПРАВИЛО ЛЕНЦА

Направление индукционного тока определяется правилом Ленца: индукционный ток всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, которое вызывает этот ток. Из этого следует, что при возрастании магнитного потока возникающий индукционный ток будет иметь такое направление, чтобы порождаемое им магнитное поле было направлено против внешнего поля, противодействуя увеличению магнитного потока. Уменьшение магнитного потока, наоборот, приводит к появлению индукционного тока, создающего магнитное поле, совпадающее по направлению с внешним полем.

Рис . 7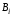

Пусть, например, в однородном магнитном поле находится квадратная рамка, изготовленная из металла и пронизываемая магнитным полем (рис.7). Предположим, что магнитное поле возрастает. Это приводит к увеличению магнитного потока через площадь рамки. Согласно правилу Ленца, магнитное поле, возникающего индукционного тока будет направлено против внешнего поля, т.е. вектор этого поля противоположен вектору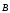. Применяя правило правого винта (если винт вращать так, чтобы его поступательное движение совпадало с направлением магнитного поля, то его вращательное движение даёт направление тока), находим направление индукционного токаI_i.