
- •КазанСкий государственный архитектурНо-строительный университет
- •Часть I. Расчет ломаного стержня
- •ЧастЬ II. Расчет внецентренно сжатого стержня
- •Пример выполнения расчетно-графической работы пример к части I. Расчет ломаного стержня Правила построения эпюр внутренних силовых факторов (всф) в стержне (брусе) при сложном сопротивлении
- •Пример построения эпюр всф
- •Подбор размеров сечений для участков бруса при сложном сопротивлении
- •Пример к части II
- •Решение
- •1. Найдем центр тяжести сечения (т.С) и главные центральные моменты инерции и.
- •Построение ядра сечения
- •Литература
- •Геометрические характеристики некоторых сечений
- •МЕтодиЧЕские указаниЯ
- •420043, Казань, ул.Зеленая, 1
Пример к части II
|
Исходные данные:
Рис.6 |
Рассмотрим стержень с поперечным сечением, показанным на рис.6. Сечение сложное, его надо разбить на прямоугольные части: 1 фигура а х ; 2 фигура с х ; 3 фигура 0,5а х . Размеры а, с, надо определять через заданный размер «b» в табл.1. Пусть получилось а = 24 см, с = 26,8см, = 2,6 см.
|
Решение
1. Найдем центр тяжести сечения (т.С) и главные центральные моменты инерции и.
Сечение имеет одну ось симметрии «Y» - она является главной осью, вторая главная ось Х перпендикулярна первой и проходит через т.С.
Введем
произвольные оси
 и
и (рис.6) с учетом симметрии фигуры. Положение
т.С
можно определить так:
(рис.6) с учетом симметрии фигуры. Положение
т.С
можно определить так:
 13,19
см, где:
13,19
см, где:
 -
суммарная площадь сечения;
-
суммарная площадь сечения;
 -
статический момент сечения относительно
оси
-
статический момент сечения относительно
оси
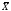 .
.
Примечание:если сечение включает прямоугольное отверстие, то при суммировании эта площадь и статический момент считаютсяотрицательными.
 см2;
см2;
 см2;
см2;
 см2;
А =
62,4+69,68+31,2 = 163,28
см.
см2;
А =
62,4+69,68+31,2 = 163,28
см.
 -
координаты центров тяжести
-
координаты центров тяжести
 каждого прямоугольника вдоль оси
каждого прямоугольника вдоль оси :
:
 1,3
см;
1,3
см;
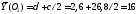 см;
см;
 см
см
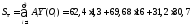 =2153,84
см3
=2153,84
см3
Определив
 находим
положение т.С
и проводим главные центральные оси ХСY.
находим
положение т.С
и проводим главные центральные оси ХСY.
Для вычисления моментов инерции используем формулу изменения моментов инерции при параллельном переносе осей (верхний индекс в скобках при J определяет номер фигуры, а нижний определяет ось):
 отсюда
отсюда

 см4
см4
 см4
см4
 см4
см4
 см4
см4
Jx
= 23165,8
см4
23165,8
см4
Все
оси
 и
и совпадают (ввиду симметрии сечения),
поэтому
совпадают (ввиду симметрии сечения),
поэтому
 3408,9
см4
3408,9
см4
 см4;
см4;
 см4;
см4;
 см4
см4
Найдем радиус инерции сечения:
 11,91
см;
11,91
см;
 4,57
см
4,57
см
Вычислим координаты точки Р приложения сжимающей силы F в главных центральных осях (см.рис.7):
 6
см;
6
см;
 16,21
см
16,21
см
Определим
положение нейтральной оси (Н.О) сечения.
Для этого вычислим отрезки
 и
и ,
которые Н.О отсекает на осях координат:
,
которые Н.О отсекает на осях координат:
 см;
см;
 см
см
Рисуем
сечение стержня в масштабе и, откладывая
на этом чертеже отрезки
 и
и с учетом знаков, найдем положение Н.О
(рис.7).
с учетом знаков, найдем положение Н.О
(рис.7).
Пронумеруем все угловые точки сечения т.1.12. Нейтральная ось делит сечение на две зоны: сжатую (где расположена т.Р, в которой действует сжимающая сила F) и растянутую. Из рис.7 видно, что в растянутой зоне максимально удаленной от Н.О будет т.6, в в сжатой зоне – т.12.
Если Н.О не пересекает сечение, то все сечение работает на сжатие (растянутой зоны нет).
|
Рис.7 |
В
любой i-той
точке сечения (с координатами
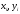 )
при внецентренном нагружении нормальные
напряжения
)
при внецентренном нагружении нормальные
напряжения можно найти по формуле:
можно найти по формуле:
 . (6)
. (6)
Условие
прочности в т.6 (х6
=
12 см, у6
=  =
13,19 см).
=
13,19 см).

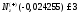 .
Отсюда найдем
.
Отсюда найдем
 - допускаемую нагрузку из условия
прочности в растянутой зоне сечения:
- допускаемую нагрузку из условия
прочности в растянутой зоне сечения:
 =
123,70 кН.
=
123,70 кН.
Условие прочности в т.12 (х12 = 6 см, у12 = Yр + = 16,21+2,6=18,81 см).

 .
Отсюда найдем
.
Отсюда найдем
 - допускаемую нагрузку из условия
прочности в сжатой зоне сечения:
- допускаемую нагрузку из условия
прочности в сжатой зоне сечения:
 =
301,8 кН.
=
301,8 кН.
Из
этих двух
 и
и за общую допускаемую нагрузку [F]
необходимо принять min
(по модулю)
за общую допускаемую нагрузку [F]
необходимо принять min
(по модулю)
Итак [F] = -123,7 кН.
Построим эпюру z в сечении колонны.
Согласно
(6)
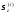 - линейно меняются по координатам точекxi
и yi
сечения. Поэтому эпюру z
можно построить по двум значениям
- линейно меняются по координатам точекxi
и yi
сечения. Поэтому эпюру z
можно построить по двум значениям
 от [F]:
от [F]:
1)
в т.6 от [F]
=
 = -123,7 кН
= -123,7 кН = 3 кН/см2.
= 3 кН/см2.
2)
в т.12 от [F]
 = [F]
(0,02982) =
3,69 кН/см2
= [F]
(0,02982) =
3,69 кН/см2
Строим
эпюру z.
Из т.6 проводим перпендикуляр к Н.О,
отрезок (6m).
В т.6 под углом 90
к (6m)
отложим
 = 3 кН/см2,
получим точку n.
Из т.12 проводим отрезок (12mL),
параллельно Н.О. Отложим
= 3 кН/см2,
получим точку n.
Из т.12 проводим отрезок (12mL),
параллельно Н.О. Отложим
 = 3,69 кН/см2,
равное отрезку (mL).
= 3,69 кН/см2,
равное отрезку (mL).
Напряжения откладывать в масштабе, смена знаков на эпюре z происходит в точке, где отрезок (Ln) пересекается с Н.О. Эпюра z показана на рис.7.


