контрольная работа №2

15

Задание 2.1.

Вычислить пределы:

а). ;

б). ;

в). .

Решение.

а). Подставляя вместо нулевое значение, получим:

.

б). Подставляя вместо нулевое значение, получаем неопределенность . Используя тригонометрические тождества преобразуем числитель: . При дальнейшем вычислении предела используем эквивалентность синуса, а именно . Тогда, получим:

.

в). Сводим указанный предел ко второму замечательному пределу, а именно к пределу вида , который равен числу Непера . Тогда, получим:

.

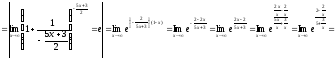
Задание 2.2.

Найти производные 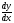данных функций:

а). ;

б). ;

в). ;

г). 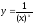; д). .

Решение.

а).

.

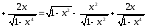б).

.

в).

.

г). .

Применяем логарифмическое дифференцирование. Прологарифмуем обе части уравнения:

.

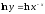Используя свойства логарифма, получим:

.

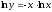Продифференцируем обе части полученного выражения:

;

; .

Тогда, получим:

; .

д). .

Имеем неявно заданную функцию двух переменных: .

Находим частные производные:

; .

Используем соответствующую формулу для нахождения производной неявно заданной функции двух переменных:

.

Задание 2.3.

Найти наибольшее и наименьшее значения функции на отрезке .

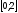Решение.

Находим производную первого порядка:

.

Приравнивая найденную производную к нулю, находим критические точки:

; ;

, , .

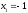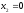Точка не принадлежит отрезку , поэтому в дальнейших расчетах ее не рассматриваем. Другие две критические точки принадлежат отрезку . Находим значения функции в этих точках, а также на концах отрезка:

;

;

.

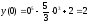Сравнивая найденные значения, делаем вывод о том, что наибольшее значение функции на указанном отрезке равно 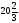, а наименьшее – .

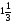Задание 2.4.

Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.

а). ;

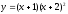б). .

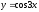Решение.

а). .

1). Область определения функции: .

2). Исследуем функцию на четность и нечетность.

, поэтому функция ни четная ни нечетная. Следовательно, ее график не будет симметричным ни относительно оси ординат, ни относительно начала координат.

3). Функция непериодическая.

4). Находим точки пересечения графика функции с осями координат.

При получим: . Следовательно, – точка пересечения графика функции с осью ординат.

При получим: ; , . Следовательно, и – точки пересечения графика функции с осью абсцисс.

5). Находим производную первого порядка и определяем критические точки.

;

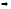
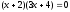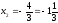; ; – критические точки.

Находим значения функции в критических точках:

; .

Разбиваем критической точкой область определения на интервалы. Строим дополнительную расчетную таблицу для определения промежутков роста и убывания функции, а также для нахождения экстремумов (при помощи определения знака производной на каждом из интервалов):

	+	0	–	0	+
		0			
		максимум		минимум

6). Находим производную второго порядка и определяем возможные точки перегиба.

;

; .

Находим значение функции в найденной точке:

Разбиваем найденными точками область определения на интервалы. Строим дополнительную расчетную таблицу для определения промежутков вогнутости и выпуклости функции, а также для нахождения точек перегиба (при помощи определения знака производной второго порядка на каждом из интервалов):

	–	0	+
	выпуклая		вогнутая
		перегиб

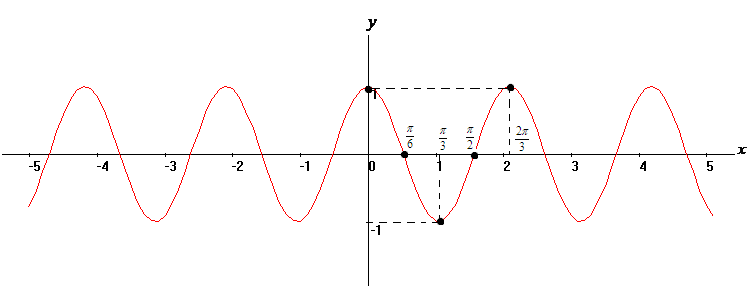
7). По результатам исследования строим график функции.

б). .

1). Область определения функции: .

2). Исследуем функцию на четность и нечетность.

, поэтому функция четная. Следовательно, ее график будет симметричным относительно оси ординат.

3). Пусть – произвольное фиксированное число. Тогда

.

Поскольку косинус является периодической функцией с основным периодом 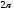, то в нашем случае получим:

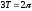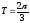; – основной период указанной функции.

Следовательно, функция – периодическая.

В дальнейшем будем исследовать функцию на отрезке (в остальных точках график функции будет повторятся).

4). Находим точки пересечения графика функции с осями координат.

При получим: . Следовательно, – точка пересечения графика функции с осью ординат.

При получим: ; ;

Для отрезка 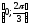получим: и .

Следовательно, 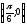и – точки пересечения графика функции с осью абсцисс.

5). Находим производную первого порядка и определяем критические точки.

;

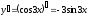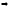
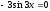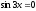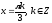; ; ; – критические точки.

Для отрезка получим две критические точки: и .

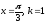Находим значения функции в критических точках:

; .

Строим дополнительную расчетную таблицу для определения промежутков роста и убывания функции, а также для нахождения экстремумов (при помощи определения знака производной на каждом из интервалов):

	+	0	–	0	+
		1		-1	
		максимум		минимум

6). Находим производную второго порядка и определяем 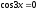возможные точки перегиба.

;

; ; – возможные точки перегиба.

Для отрезка 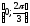получим: и .

Строим дополнительную расчетную таблицу для определения промежутков вогнутости и выпуклости функции, а также для нахождения точек перегиба (при помощи определения знака производной второго порядка на каждом из интервалов):

	–	0	+	0	–
	выпуклая	0	вогнутая	0	выпуклая
		перегиб		перегиб

7). По результатам исследования строим график функции.