контролая работа №3

4

Задание 3.1.

Дана функция . Показать, что .

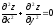Решение.

Находим частные производные первого порядка:

;

.

Находим частные производные второго порядка:

;

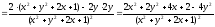
Следовательно,

, что и требовалось показать.

Задание 3.2.

Дана функция и точка . Найти grad 𝑧 в точке .

Решение.

Сначала находим частные производные первого порядка в точке :

, ;

, .

Градиент функции в точке находим, используя соответствующую формулу:

.

Следовательно, .

Ответ:

Задание 3.3.

Дана функция и вектор . Найти производную в точке по направлению вектора .

Решение.

Сначала находим частные производные первого порядка в точке :

, ;

, .

Находим косинусы углов между направлением вектора и положительными направлениями двух координатных осей:

, .

Производная в точке по направлению:

.