
- •Министерство образования и науки рф фгбоу впо «Казанский государственный архитектурно-строительный университет»
- •Введение
- •1. Указания к оформлению работы
- •2. Задания к выполнению задач
- •3. Методические указания к выполнению работы. Примеры расчета
- •3.1. Задача №1. Определение напряжений в грунте от действия сосредоточенных сил
- •3.2. Задача №2. Определение напряжений в грунте методом угловых точек
- •3.3. Задача №3. Определение напряжений в грунте от действия равномерно распределенной нагрузки
- •Пример расчета
- •3.4. Задача №4. Определение давления грунта на подпорную стенку
- •3.4.1. Определение давления на подпорную стенку от идеально сыпучего грунта
- •Пример расчета
- •Пример расчета
- •3.6. Задача №6. Расчет осадки методом эквивалентного слоя (метод н.А. Цытовича)
- •Определение затухания осадки во времени
- •Литература
- •Приложения Приложение 1
- •Приложение 2
- •Глубина заложения фундаментов по условиям морозного пучения грунтов
- •Приложение 5 Классификация пылевато-глинистых грунтов по показателю текучести, jl
- •Расчетные сопротивления r0 пылевато-глинистых (непросадочных) грунтов
- •Нормативные значения модуля деформации е (мПа) пылевато-глинистых грунтов
- •Предельные деформации основания
- •420043, Казань, Зеленая, 1
3. Методические указания к выполнению работы. Примеры расчета
3.1. Задача №1. Определение напряжений в грунте от действия сосредоточенных сил
Для
случая, когда к горизонтальной поверхности
массива грунта приложено несколько
сосредоточенных сил
![]() ,
величины вертикальных составляющих
напряжений
,
величины вертикальных составляющих
напряжений![]() в любой точке массива грунта можно
определить суммированием составляющих
напряжений от действия каждой силы в
отдельности с использованием зависимости
в любой точке массива грунта можно
определить суммированием составляющих
напряжений от действия каждой силы в
отдельности с использованием зависимости
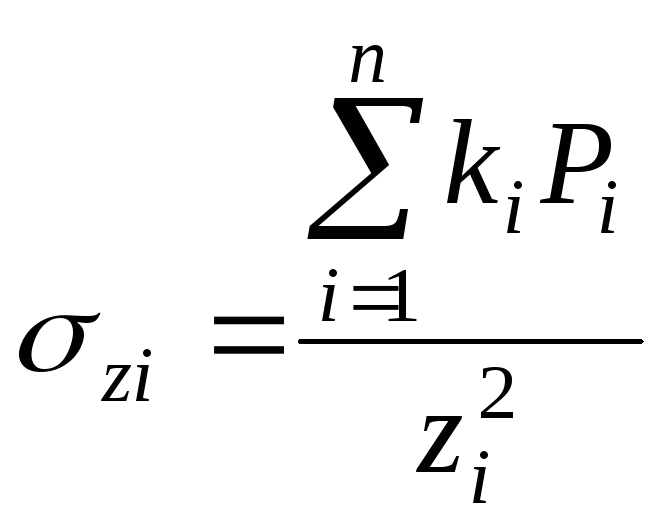 , (3.1.1)
, (3.1.1)
где
![]() -
коэффициент, являющийся функцией
отношения
-
коэффициент, являющийся функцией
отношения![]() ;
;
![]() -
расстояние по горизонтальной оси от
рассматриваемой точки до оси
-
расстояние по горизонтальной оси от
рассматриваемой точки до оси
![]() ,
проходящей через точку приложения
сосредоточенной силы
,
проходящей через точку приложения
сосредоточенной силы![]() ;
;
![]() -
глубина рассматриваемой точки от
плоскости приложения сосредоточенной
силы
-
глубина рассматриваемой точки от
плоскости приложения сосредоточенной
силы
![]() .
.
Значения
коэффициента
![]() приведены
в табл.4.1 [2], табл.3.1 [5] или в таблице 1.1
приложения настоящих методических
указаний.
приведены
в табл.4.1 [2], табл.3.1 [5] или в таблице 1.1
приложения настоящих методических
указаний.
При построении расчетной схемы и эпюр напряжений следует принимать масштаб расстояний 1:50, масштаб напряжений 0,05 МПа в 1 см.
Пример расчета
Дано:
![]()
Решение. Определяем напряжения в точках, расположенных по вертикали I-I.
Точка 1 z=1 м.
r1 =2 м r1/z=2/1=2 k1=0,0085
r2=0 r2/z=0/1=0 k2=0,4775
r3=3 м r3/z=3/1=3 k3=0,0015
![]()
Точка 2 z=2 м.
r1 =2 м r1/z=2/2=1 k1=0,0844
r2=0 r2/z=0/2=0 k2=0,4775
r3=3 м r3/z=3/2=1,5 k3=0,0251
![]()
Точка 3 z=3 м.
r1 =2 м r1/z=2/3=0,6667 k1=0,1889
r2=0 r2/z=0/3=0 k2=0,4775
r3=3 м r3/z=3/3=1 k3=0,0844
![]()
Точка 4 z=4 м.
r1 =2 м r1/z=2/4=0,5 k1=0,2733
r2=0 r2/z=0/4=0 k2=0,4775
r3=3 м r3/z=3/4=0,75 k3=0,1565
![]()
Точка 5 z=6 м.
r1 =2 м r1/z=2/6=0,33 k1=0,3687
r2=0 r2/z=0/6=0 k2=0,4775
r3=3 м r3/z=3/6=0,5 k3=0,2733
![]()
Определяем напряжения в точках расположенных по горизонтали II-II.
Точка 6 z=3 м.
r1 =1 м r1/z=1/3=0,33 k1=0,3687
r2=3 м r2/z=3/3=1 k2=0,0844
r3=6 м r3/z=6/3=2 k3=0,0085
![]()
Точка 7 z=3 м.
r1 =1 м r1/z=1/3=0,33 k1=0,3687
r2=1 м r2/z=1/3=0,33 k2=0,3687
r3=4 м r3/z=4/3=1,33 k3=0,0374
![]()
Точка 8 z=3 м.
r1 =3 м r1/z=3/3=1 k1=0,0844
r2=1 м r2/z=1/3=0,33 k2=0,3687
r3=2 м r3/z=2/3=0,67 k3=0,1889
![]()
Точка 9 z=3 м.
r1 =5 м r1/z=5/3=1,67 k1=0,0171
r2=3 м r2/z=3/3=1 k2=0,0844
r3=0 r3/z=0/3=0 k3=0,4775
![]()
По полученным значениям напряжений строим эпюры распределения напряжений по соответствующим точкам (рис.3.1).
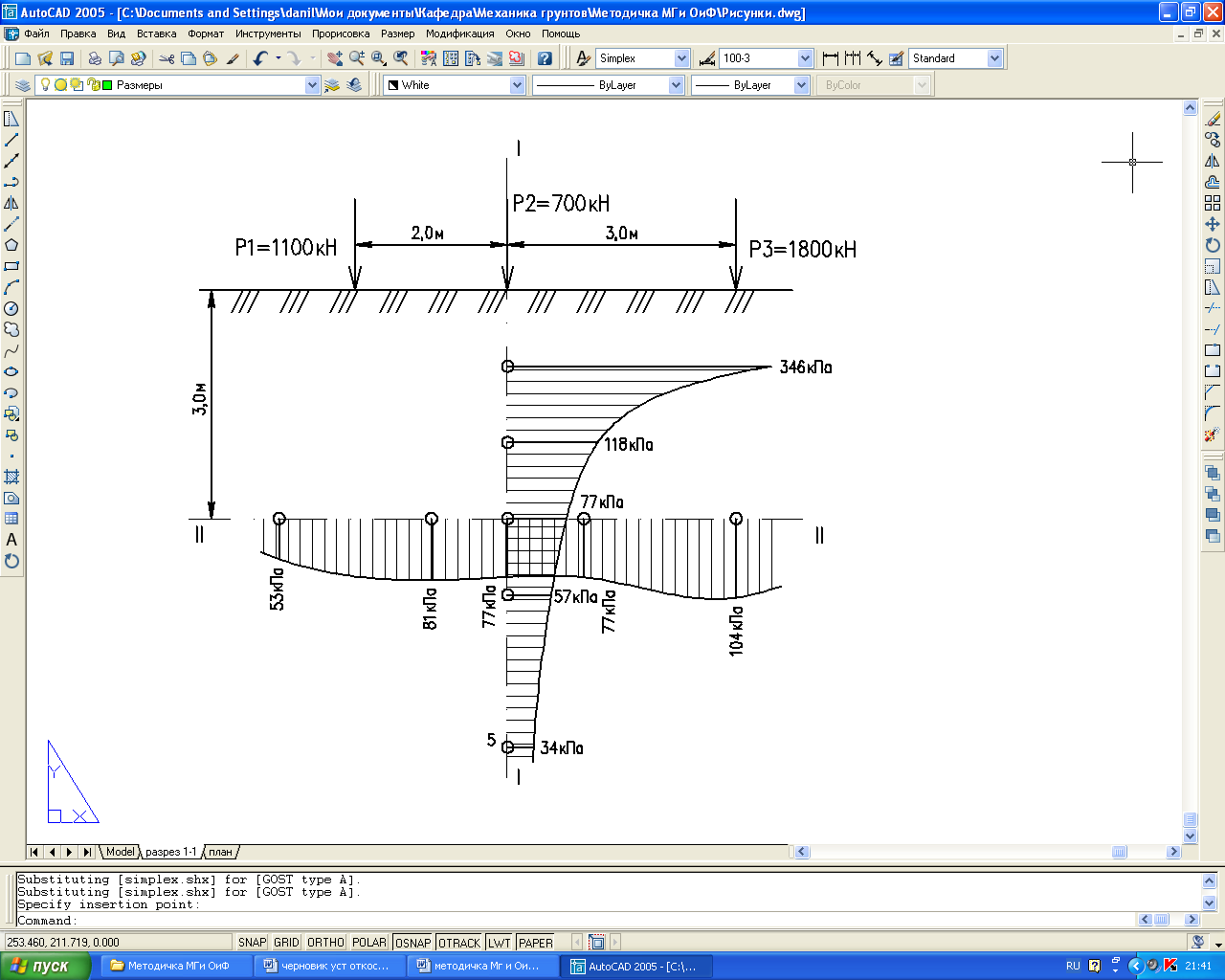
Рис. 3.1. Эпюры напряжений
3.2. Задача №2. Определение напряжений в грунте методом угловых точек
Распределение
по глубине вертикальных составляющих
напряжений
![]() в любой точке массива грунта от действия
равномерно распределенной нагрузки в
пределах или за пределами плит нагружения
может быть определено по методу угловых
точек по формуле
в любой точке массива грунта от действия
равномерно распределенной нагрузки в
пределах или за пределами плит нагружения
может быть определено по методу угловых
точек по формуле
![]() , (3.2)
, (3.2)
где
![]() - коэффициент, определяемый в зависимости
от отношения сторон прямоугольной
площади загружения
- коэффициент, определяемый в зависимости
от отношения сторон прямоугольной
площади загружения![]() (
(![]() – длинная ее сторона,
– длинная ее сторона,![]() – ее ширина) и отношения
– ее ширина) и отношения![]() (
(![]() -
глубина, на которой определяется
напряжение
-
глубина, на которой определяется
напряжение![]() );
);
![]() -
интенсивность равномерно распределенной
нагрузки.
-
интенсивность равномерно распределенной
нагрузки.
В
соответствии с этим заданные плиты
нагружения разбивают на прямоугольники
таким образом, чтобы они имели общую
угловую точку, через которую проходит
расчетная вертикаль
![]() .
Для каждого из этих прямоугольников со
сторонами
.
Для каждого из этих прямоугольников со
сторонами![]() с помощью таблиц определяют значения
коэффициента
с помощью таблиц определяют значения
коэффициента![]() и, пользуясь принципом независимости
действия сил, находят алгебраическим
суммированием напряжения в заданных
точках массива. Значения коэффициента
и, пользуясь принципом независимости
действия сил, находят алгебраическим
суммированием напряжения в заданных
точках массива. Значения коэффициента![]() приведены в табл.3.5 [5] и в табл.1.2 приложения
настоящих методических указаний.
приведены в табл.3.5 [5] и в табл.1.2 приложения
настоящих методических указаний.
Масштаб расстояний 1:50, масштаб напряжений 0,05 МПа в 1 см.
Пример расчета
Дано:
![]() расчетная
вертикаль М3.
расчетная
вертикаль М3.
Решение. Заданные плиты нагружения разбиваем на прямоугольники таким образом, чтобы они имели общую угловую точку, через которую проходит расчетная вертикаль М3 (рис. 2.2). Таким образом, имеем 5 прямоугольников:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
Искомые напряжения найдем, суммируя напряжения от действия нагрузки по прямоугольникам 1, 2, 3 взятым со знаком «плюс» и напряжения от действия нагрузки по прямоугольникам 4, 5 со знаком «минус».
z=1 м
1.
![]() 2,5/1,9=1,32,
2,5/1,9=1,32,![]() 1/1,9=0,53,
1/1,9=0,53,![]() 0,2352.
0,2352.
2.
![]() 1,31,
1,31,![]() 0,31,
0,31,![]() 0,2457.
0,2457.
3.
![]() 1,86,
1,86,![]() 0,57,
0,57,![]() 0,232.
0,232.
4.
![]() 9,44,
9,44,![]() 2,22,
2,22,![]() 0,128.
0,128.
5.
![]() 3,89,
3,89,![]() 2,22,
2,22,![]() 0,1251.
0,1251.
![]()
z=2 м
1.
![]() 1,32,
1,32,![]() 1,06,
1,06,![]() 0,1782.
0,1782.
2.
![]() 1,31,
1,31,![]() 0,62,
0,62,![]() 0,2286.
0,2286.
3.
![]() 1,86,
1,86,![]() 1,14,
1,14,![]() 0,1983.
0,1983.
4.
![]() 9,44,
9,44,![]() 4,4,
4,4,![]() 0,069.
0,069.
5.
![]() 3,89,
3,89,![]() 4,4,
4,4,![]() 0,0597.
0,0597.
![]()
z=4 м
1.
![]() 1,32,
1,32,![]() 2,11,
2,11,![]() 0,0933.
0,0933.
2.
![]() 1,31,
1,31,![]() 1,23,
1,23,![]() 0,1654.
0,1654.
3.
![]() 1,86,
1,86,![]() 2,28,
2,28,![]() 0,1009.
0,1009.
4.
![]() 9,44,
9,44,![]() 8,89,
8,89,![]() 0,0316.
0,0316.
5.
![]() 3,89,
3,89,![]() 8,89,
8,89,![]() 0,0199.
0,0199.
![]()
z=6 м
1.
![]() 1,32,
1,32,![]() 3,16,
3,16,![]() 0,0508.
0,0508.
2.
![]() 1,31,
1,31,![]() 1,85,
1,85,![]() 0,1013.
0,1013.
3.
![]() 1,86,
1,86,![]() 3,43,
3,43,![]() 0,0571.
0,0571.
4.
![]() 9,44,
9,44,![]() 13,3,
13,3,![]() 0,0155.
0,0155.
5.
![]() 3,89,
3,89,![]() 13,3,
13,3,![]() 0,0084.
0,0084.
![]()
По
полученным значениям напряжений строим
эпюру распределения напряжений
![]() (рис.3.2).
(рис.3.2).
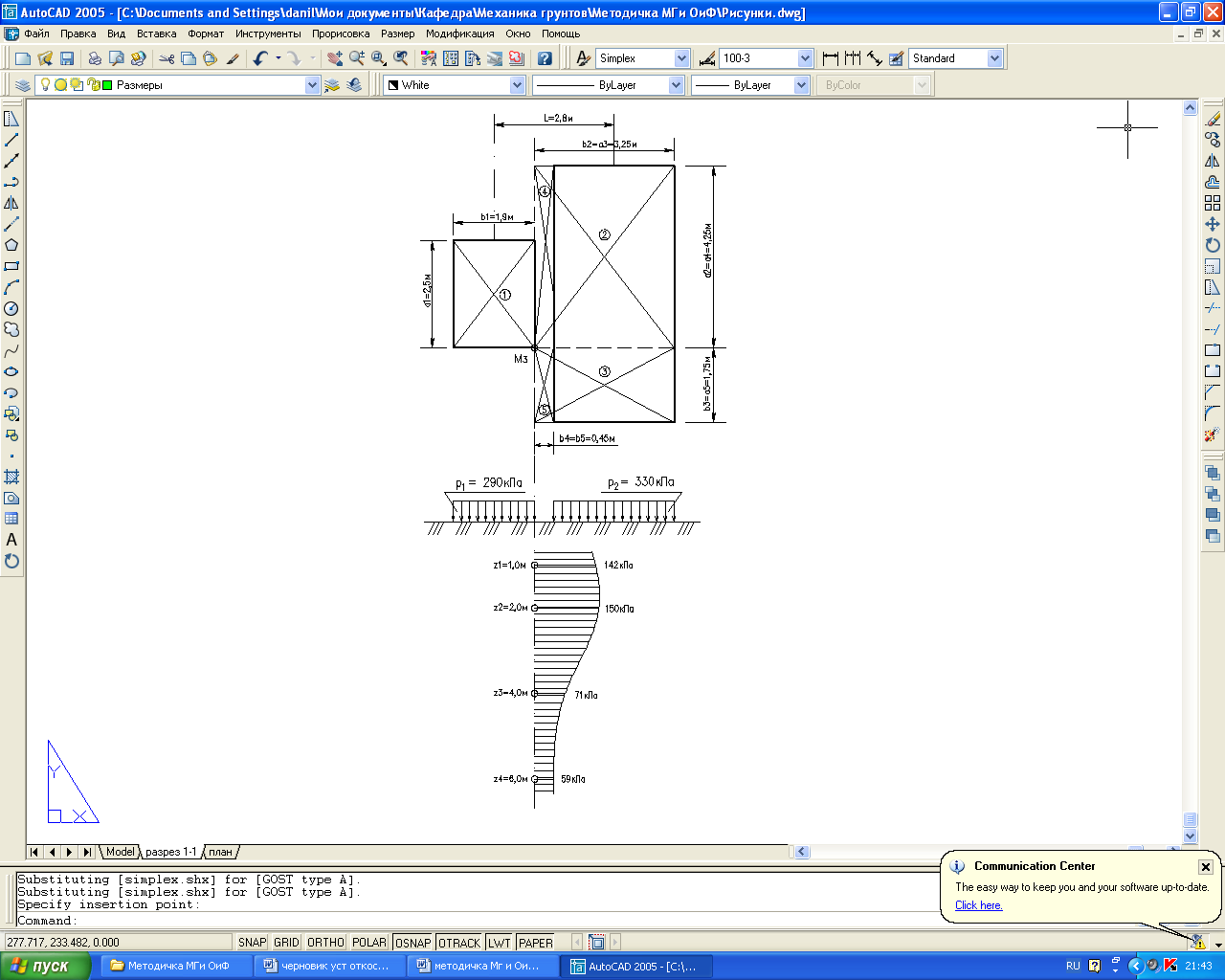
Рис.3.2. Эпюра напряжений
