
- •Федеральное агенство по образованию
- •270114, 270115, 270201, 240400, 290600, 291000
- •2009 Основные понятия и формулы
- •Изменение геметрических характеристик при преобразовании прямоугольных координат
- •Порядок вычислеия геометрических характеристик сложных поперечных сечений
- •Пример определения геометрических характеристик сложного поперечного сечения
- •Исходные данные:
- •Решение
- •Контрольные вопросы по теме «геометрические характеристики поперечного сечения»
- •Решение некоторых типовых задач
- •Решение
- •Решение
- •Геометрические характеристики простейших поперечных сечений
Пример определения геометрических характеристик сложного поперечного сечения

Исходные данные:
Двутавр №16 (ГОСТ 8239-72)
Равнобокий уголок 80 x 80x 6 (ГОСТ 9509-72)
Прямоугольник 200 x 20
Решение
1)
Расположим составное сечение (рис.6) в
первой четверти координатной плоскости
![]() (чтобы в дальнейшем не ошибиться со
знаками вычисляемых геометрических
характеристик).
(чтобы в дальнейшем не ошибиться со
знаками вычисляемых геометрических
характеристик).
2) Пронумеруем фигуры:
прямоугольник - (фигура 1), двутавр - (фигура 2), равнобокий уголок - ( фигура 3).
Проведем для каждой
фигуры собственные центральные оси
![]() ( рис.6, рис.11).
( рис.6, рис.11).
Д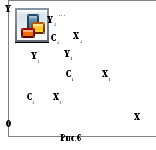 ля
прямоугольника и двутавра эти оси будут
и главными осями, так как у каждой из
этих фигур есть оси симметрии.
ля
прямоугольника и двутавра эти оси будут
и главными осями, так как у каждой из
этих фигур есть оси симметрии.
Для каждой фигуры
найдем все необходимые геометрические
характеристики и координаты центра
тяжести относительно первоначальных
осей
![]() .
.
а) Прямоугольник (фигура1)
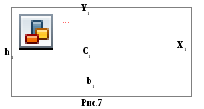
![]() =200мм=20см,
=200мм=20см,
![]() =20мм=2см,
=20мм=2см,
![]() ,
,
![]() ,
,![]()
![]() (т.к. оси
(т.к. оси![]() являются главными центральными).
являются главными центральными).
б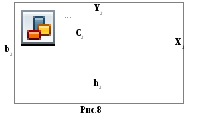 )
Двутавр № 16 (фигура 2)
)
Двутавр № 16 (фигура 2)
![]()
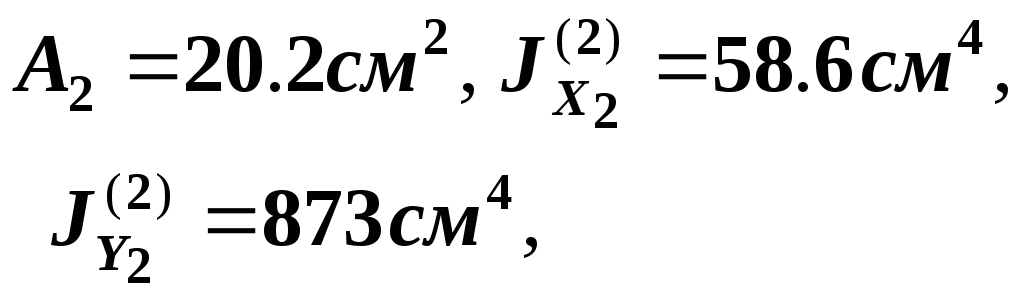
![]() (т.к. оси
(т.к. оси
![]() являются главными центральными).
являются главными центральными).
Замечание: при
выборе
![]() для двутавра и швеллера необходимо
учитывать, что их табличное расположение
может отличаться от рассматриваемого.
В частности если имеем:
для двутавра и швеллера необходимо
учитывать, что их табличное расположение
может отличаться от рассматриваемого.
В частности если имеем:
а) вертикальное расположение швеллера(двутавра), то:
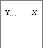
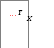
![]()
б) горизонтальное расположение швеллера (двутавра),то:
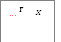
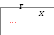
![]()
в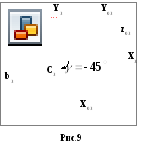 )Равнобокий
уголок 80x80x6
(фигура 3)
)Равнобокий
уголок 80x80x6
(фигура 3)
![]()
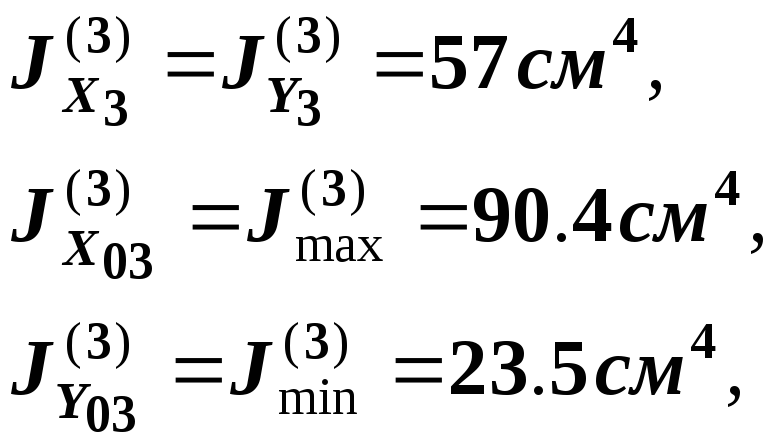
![]() (т.к. оси
(т.к. оси
![]() являются главными центральными для
равнобокого уголка).
являются главными центральными для
равнобокого уголка).
Определим
центробежный момент
![]() .
Для этого воспользуемся первым (или
вторым) соотношением из (14). Знак угла
.
Для этого воспользуемся первым (или
вторым) соотношением из (14). Знак угла![]() определяется направлением поворота от
центральной оси к главной.
определяется направлением поворота от
центральной оси к главной.
![]() ,
если поворот от оси
,
если поворот от оси
![]() к оси
к оси![]() происходит по часовой стрелке;
происходит по часовой стрелке;
![]() ,
если поворот от оси
,
если поворот от оси
![]() к оси
к оси![]() происходит против часовой стрелки;
происходит против часовой стрелки;
Подставляя в первое соотношение из (14), получим:
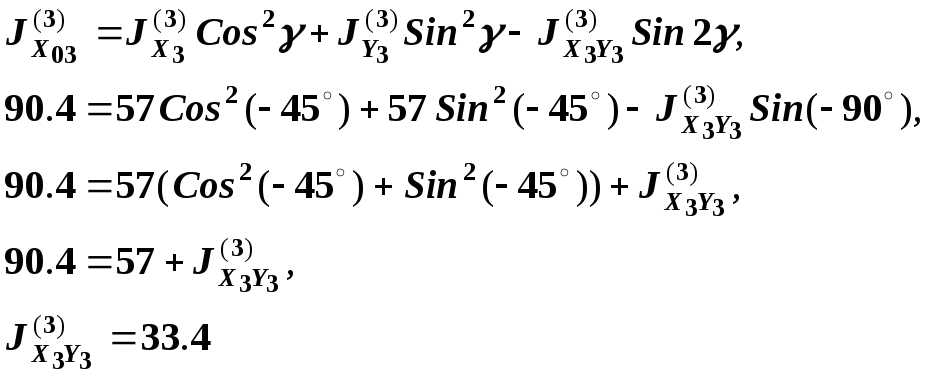
Таким образом,
центробежный момент относительно
центральных осей
![]() равен
равен![]() .
.
Замечание:
знак
центробежного момента относительно
осей
![]() (см.рис.10) определяется в зависимости
от расположения уголка относительно
этих осей.
(см.рис.10) определяется в зависимости
от расположения уголка относительно
этих осей.
Для уголка в
нашем примере (см на рис.10а)), большая
часть сечения (заштрихованная) расположена
в 1-oй
четверти где
![]() и в 3-ей четверти, где
и в 3-ей четверти, где![]() .
.
Т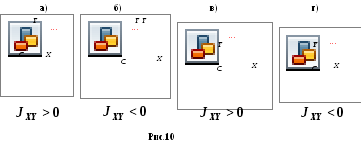 аким
образом, по определению (
аким
образом, по определению (![]() )
для всего сечения центробежный момент
)
для всего сечения центробежный момент![]() .
.
г)
Определим координаты центров тяжести
![]() ,
,![]() у каждой фигуры относительно первоначальных
осей
у каждой фигуры относительно первоначальных
осей![]() :
:
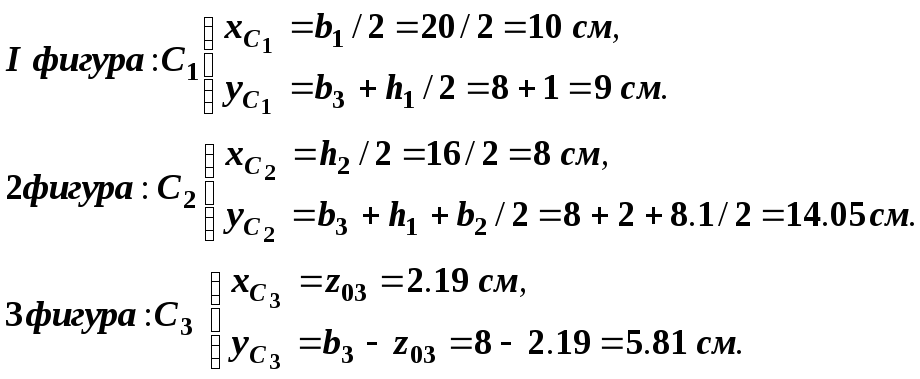
3)
Вычислим координаты центра тяжести
всей фигуры относительно первоначальных
осей
![]() ,
т.е. координаты
,
т.е. координаты![]() :
:
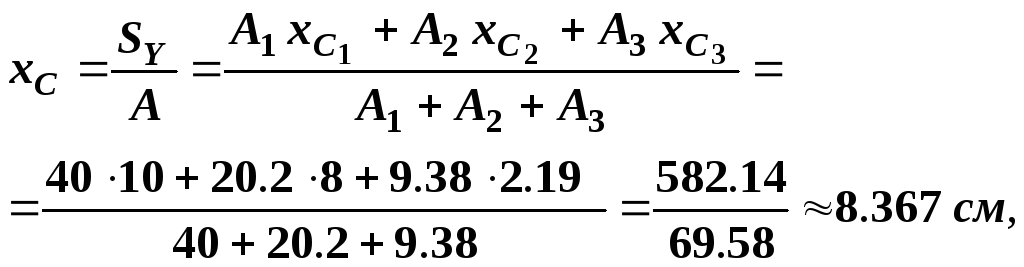
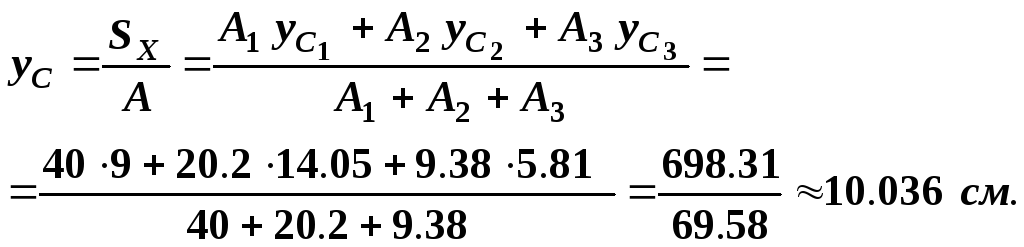
По координатам
![]() находим точку
находим точку![]() относительно
относительно![]() и
через нее проводим центральные оси
и
через нее проводим центральные оси![]() ,
параллельно первоначальным осям
(рис.11).
,
параллельно первоначальным осям
(рис.11).
4)
Вычислим моменты инерции каждой простой
фигуры относительно первоначальных
осей
![]() по формулам параллельного переноса
(10) и просуммируем моменты инерции
согласно (11).Таким образом:
по формулам параллельного переноса
(10) и просуммируем моменты инерции
согласно (11).Таким образом:
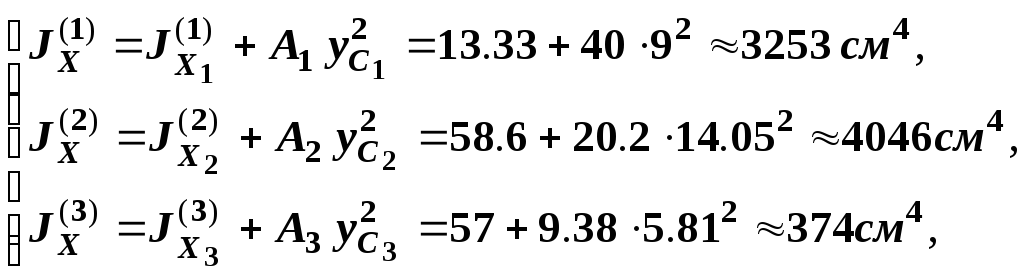
Таким образом,
![]()
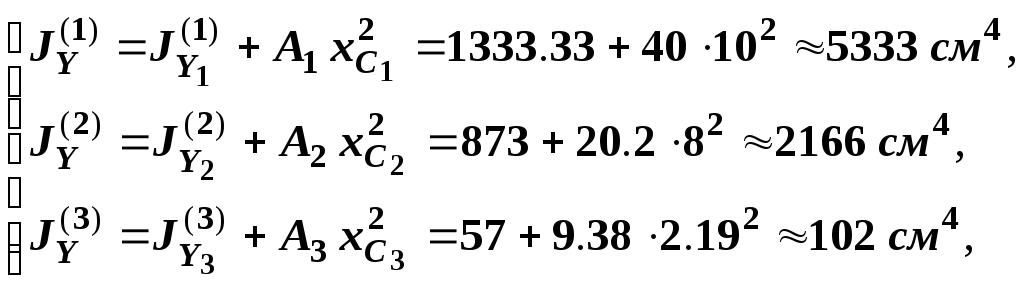
Так,
![]()
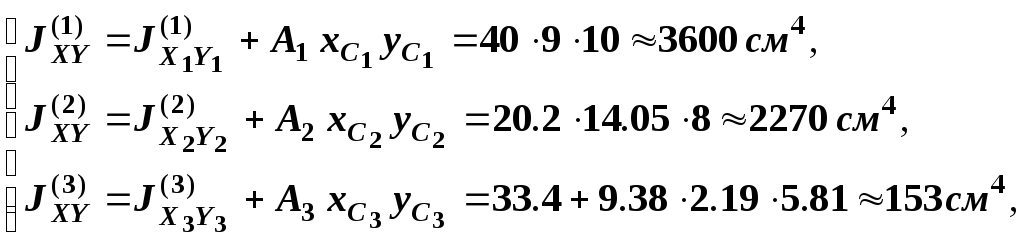
Просуммируем,
![]()
5)
Вычислим моменты инерции всего сечения
относительно центральных осей
![]() и
и![]() по формулам (12):
по формулам (12):

6)
Определим положение главных центральных
осей сечения
![]() .
Главная центральная ось сечения
.
Главная центральная ось сечения![]() расположена под углом
расположена под углом![]() к центральной оси
к центральной оси![]() согласно (13):
согласно (13):
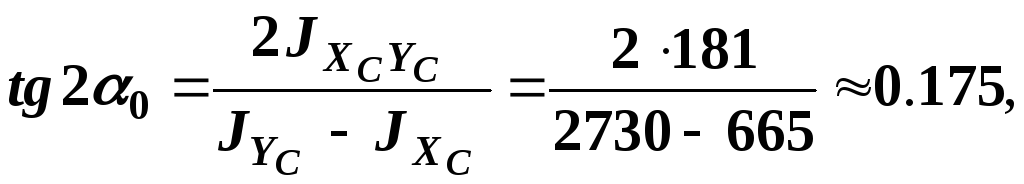
![]() (17)
(17)
Таким образом,
главные центральные оси
![]() повернуты относительно центральных
осей
повернуты относительно центральных
осей![]() на угол
на угол![]() (см. рис.11) против хода часовой стрелки
(так как угол положителен).
(см. рис.11) против хода часовой стрелки
(так как угол положителен).
7) Вычислить главные моменты инерции сложного сечения по (14):
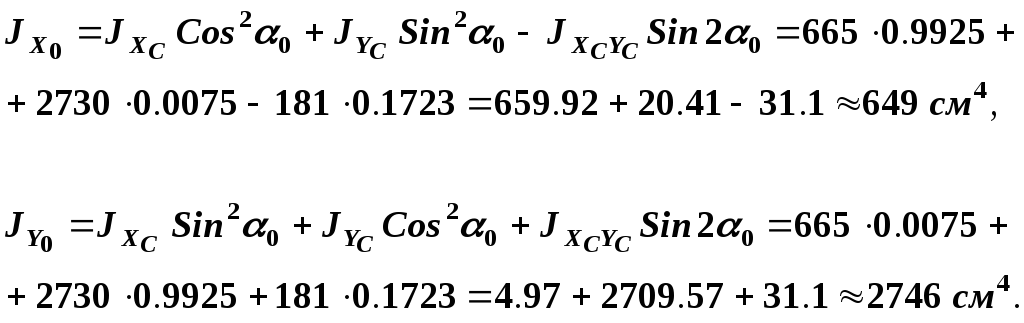 (18)
(18)
Проверка арифметических вычислений в (17) и (18).
а) Из последнего соотношения (14):
![]()
б) Согласно соотношениям (16):
![]() ,
,
![]()
Таким образом, имеет место равенство:
![]()
Итак,
![]()
8).
Определим моменты инерции относительно
центральных осей
![]() ,
расположенных под углом
,
расположенных под углом![]() (
(![]() )
к главным центральным осям
)
к главным центральным осям![]() .
.
Согласно соотношениям (15):
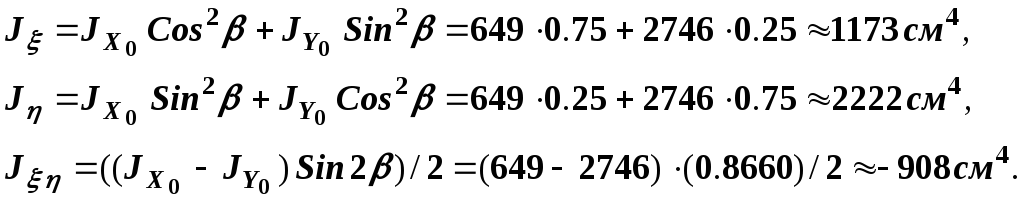
Произведем проверку последних вычислений:
![]()
![]()
Вычислим радиусы инерции сечения относительно главных осей.
![]() -
откладываем на оси
-
откладываем на оси
![]() от точки
от точки![]()
![]() - откладываем на
оси
- откладываем на
оси
![]() от точки
от точки![]()
На этих осях строим эллипс инерции (рис.11)
Заключение
Положение главных центральных осей
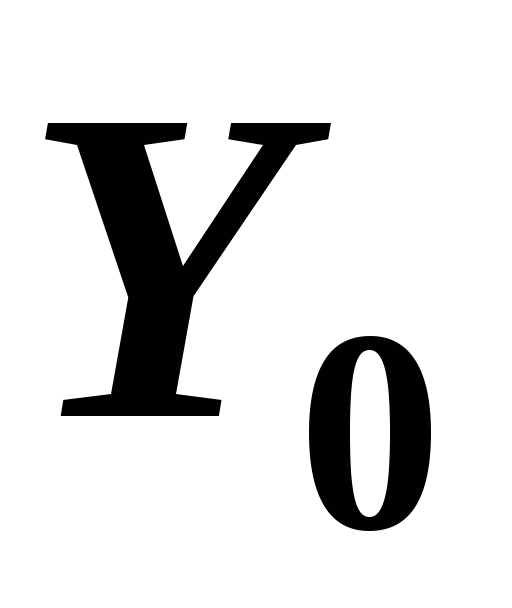 ,
,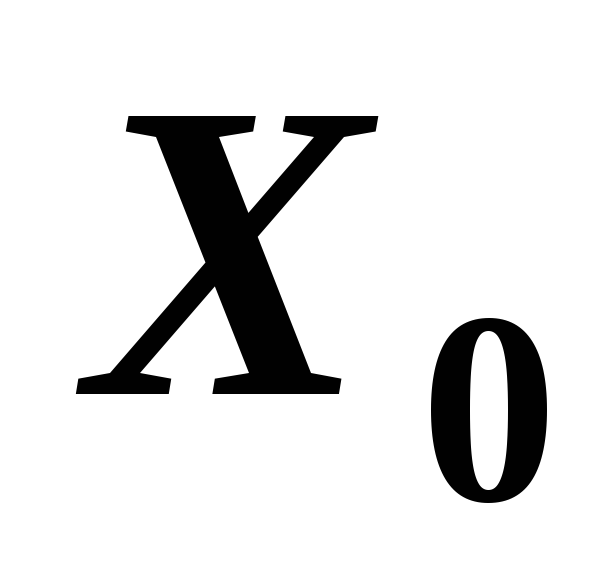 показано на рис.11. Главные моменты
инерции сечения равны
показано на рис.11. Главные моменты
инерции сечения равны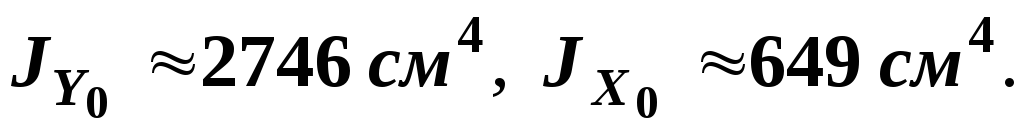
Положение эллипса инерции сечения говорит о том, что при изгибе балки в направлении оси
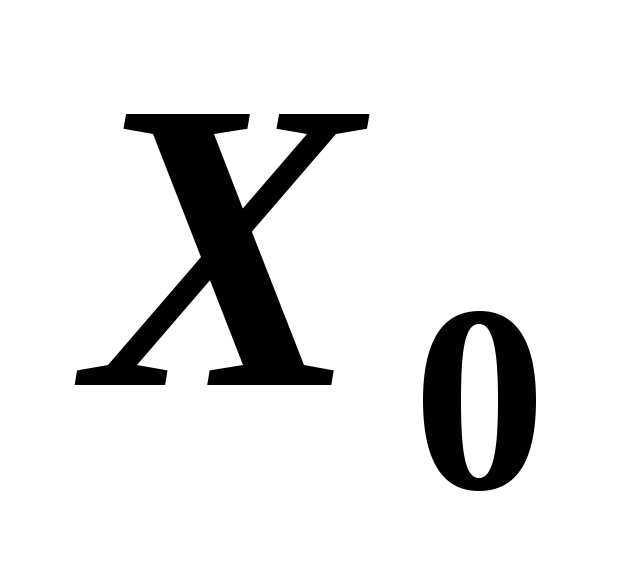 ее жесткость и прочность будут
наибольшими, а при изгибе в направлении
оси
ее жесткость и прочность будут
наибольшими, а при изгибе в направлении
оси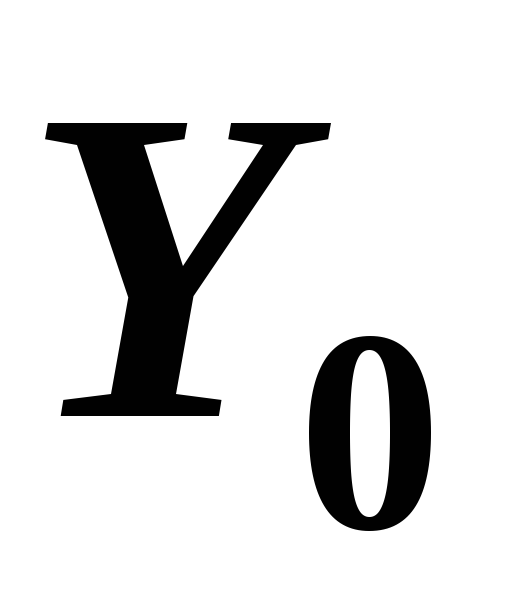 - наименьшими.
- наименьшими.
Примечание
Данная задача может быть легко алгоритмизирована и записана в виде программы для ЭВМ. Этот пример был проcчитан с помощью пакета Mathematica 5 (см. Приложение 2

