
Лекция 11. Функция и плотность распределения
.pdf1
Лекция 11. Функция и плотность распределения
11.1. Функция распределения
Непрерывную случайную величину нельзя задать законом распределения. Поэтому вводят понятие функции распределения.
Функцией распределения случайной величины X называют функцию
F (x) , определяющую вероятность того, что случайная величина X примет значение, меньшее x , то есть, F(x) P(X x) .
Геометрически это означает, что случайная величина X изображается на числовой оси точкой, которая лежит левее точки изображающей x .
Теперь определение непрерывной функции можно сформулировать так: Случайную величину называют непрерывной, если ее функция распределения есть непрерывная функция.
Функция распределения обладает свойствами:
Свойство 1. Значение функции распределения принадлежит отрезку от
нуля до единицы, то есть, 0 F(x) 1. |
|
|
|
|
|||
Это свойство вытекает из того, что F (x) |
есть вероятность. |
||||||
Свойство 2. Функция распределения есть неубывающая функция, то |
|||||||
есть, F(x2 ) F(x1 ) , если x2 |
x1 . |
|
|
|
|
||
Пусть x2 x1 , тогда, |
событие X x2 можно разбить на два несовместных |
||||||
события |
X x1 |
и |
x1 X x2 . |
По |
|
теореме |
сложения имеем: |
P(X x2 ) P(X x1 ) P(x1 X x2 ) , откуда |
P(x1 X x2 ) P(X x2 ) P(X x1 ) |
||||||
или P(x1 X x2 ) F(x2 ) F(x1 ) . |
|
|
|
|
|||
Так |
как |
любая |
вероятность |
есть |
число |
неотрицательное, то |
|
F(x2 ) F(x1 ) 0 или F(x2 ) F(x1 ) .
Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в промежутке от числа a до числа b , равна
2
приращению |
функции |
распределения |
на |
этом |
промежутке |
P(a X b) F(b) F(a) . |
|
|
|
|
|
Это свойство вытекает из полученного при доказательстве теоремы равенства P(x1 X x2 ) F(x2 ) F(x1 ) , если положить в нем x1 a и x2 b .
Пример 1. Случайная величина X задана функцией распределения
|
|
0 |
|
если |
x 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (x) |
|
|
|
если |
1 x 3, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
если |
x 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти вероятность |
того, |
что |
X примет значение, принадлежащее |
||||||||||||||||||||
промежутку (0;2) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
На интервале (0;2) |
|
функция распределения имеет вид |
F (x) |
|
x |
|
1 |
, |
|||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
|
||
следовательно, |
|
|
|
|
искомая |
|
|
вероятность |
|
равна |
|||||||||||||
P(0 x 1) F(2) F(0) |
2 |
|
1 |
( |
0 |
|
1 |
) |
|
1 |
. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
4 |
|
4 |
4 |
4 |
|
2 |
|
|
|
|
|
|
|
|||||
Следствие 2. Вероятность того, что непрерывная случайная величина
X примет определенное значение равна нулю Р(X x1 ) 0 .
Свойство 3. Если возможные значения случайной величины
принадлежат интервалу (a;b) , то : F(x) 0 |
при значениях x a |
и F(x) 1 при |
||
значениях x b . |
|
|
|
|
Пусть |
x a , тогда событие |
X x невозможное по |
условию и |
|
Р( X x) 0 |
F(x) 0 .Теперь пусть |
x b |
тогда событие X x |
достоверное |
по условию и Р(X x) 1 F(x) 1.
Следствие. Если возможные значения непрерывной случайной
величины расположены по всей числовой оси, то lim F(x) 0 , lim F(x) 1 .
x x
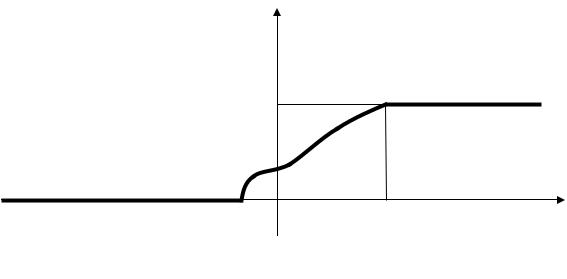
Используя доказанные свойства можно построить график функции распределения (рис.1). Из свойства 1 функции распределения вытекает, что ее график расположен между двумя прямыми линиями y 0 и y 1, Из свойства 2 вытекает, что график F (x) монотонно возрастает. А на основании
3
свойства 3 можно сделать вывод, что при |
x a |
график |
функции |
распределения имеет уравнение y 0 , при |
x b |
график |
функции |
распределения имеет уравнение y 1. |
|
|
|
y |
|
|
|
1
a O |
b |
x |
Рис. 1. График функции распределения |
|
|
График функции распределения дискретной случайной величины имеет ступенчатый вид.
Пример 2. Дискретная случайная величина X задана законом распределения
X |
1 |
4 |
8 |
|
|
|
|
P |
0,3 |
0,1 |
0,6 |
|
|
|
|
Найти функцию распределения и построить ее график.
11.2. Плотность распределения вероятностей
Непрерывную случайную величину можно задать не только функцией распределения, но и при помощи другой функции, которую называют плотностью распределения, или интегральной функцией, или плотностью вероятностей.
Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f (x) , равную первой производной от функции распределения F (x) , то есть, f (x) F (x) .
4
Дискретную случайную величину этой функцией задать нельзя.
Как видим, функция распределения является первообразной для
плотности распределения.
Теорема. Вероятность того, что непрерывная случайная величина X
примет значение, принадлежащее интервалу (a;b) , равна определенному
интегралу |
от плотности распределения, взятому |
от значения |
a до b . |
|
b |
|
|
P(a X b) f (x)dx . |
|
|
|
|
a |
|
|
|
b |
b |
|
|
|
|
|
Действительно, P(a X b) F (b) F (a) F (x)dx f (x)dx . |
|
||
|
a |
a |
|
Геометрически этот результат можно истолковать так: вероятность |
|||
того, что |
непрерывная случайная величина |
примет |
значение, |
принадлежащее интервалу (a;b) , равна площади криволинейной трапеции,
ограниченной осью Ox , графиком функции |
f (x) |
и прямыми линиями x a и |
||||||||||||||||||
x b . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зная |
плотность |
распределения |
f (x) , |
|
|
можно |
найти функцию |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
распределения F (x) по формуле F (x) f (t)dt . |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3. Найти функцию распределения и построить ее график по |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
при |
x a, |
|
|
||||
данной плотности распределения |
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||
f (x) |
|
|
при |
a x b, |
||||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
b a |
|
|
x b. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
при |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
Воспользуемся формулой F (x) f (t)dt . |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
x a , |
то |
|
f (x) 0 , следовательно, |
F(x) 0 . |
Если a x b , то |
||||||||||||||
|
|
1 |
|
|
|
|
|
|
x |
a |
|
|
x |
|
1 |
|
x a |
|
||
f (x) |
|
|
, следовательно, F (x) f (t)dt 0dx |
|
dx |
. |
||||||||||||||
b |
a |
|
|
|
|
|
|
|
|
|
a |
b a |
b a |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Если |
|
x b , |
|
то |
|
f (x) 0 , |
следовательно, |
|||||||||||||
|
x |
|
|
a |
b |
|
1 |
x |
|
b a |
|
|
|
|
|
|
|
|
|
|
F (x) f (t)dt 0dx |
|
dx 0dx |
|
1. |
|
|
|
|
|
|
|
|
||||||||
b a |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
a |
b |
b a |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5
Итак, |
|
функция |
распределения |
задается |
формулой |
|
0 |
при |
x a, |
|
|
|
|
x a |
|
|
|
|
|
|
F (x) |
|
при |
a x b, |
|
|
|
|
|
|
|
|||
b a |
|
x b. |
|
|
|
|
|
1 |
при |
|
|
|
|
|
|
|
|
|
|
|
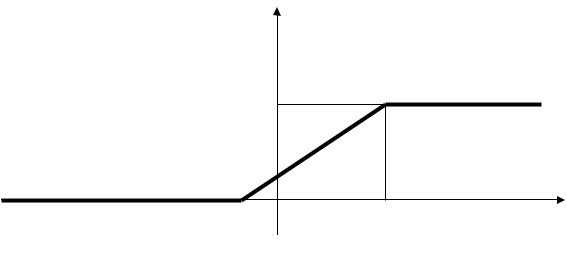
График функции распределения изображен на рис.2.
y
1
a O b x
Рис. 2. График функции распределения примера 1.
Плотность распределения обладает свойствами.
Свойство1. Плотность распределения неотрицательная функция:
f (x) 0 .
Действительно, функция распределения неубывающая, следовательно,
ее производная F (x) f (x) является неотрицательной функцией.
Из свойства 1 следует, что график плотности распределения расположен либо над осью Ox , либо на ней. График плотности распределения y f (x) называют кривой распределения.
Свойство 2. Несобственный интеграл от плотности распределения в
пределах от до равен единице f (x)dx 1.
Действительно, интеграл f (x)dx выражает вероятность события,
состоящего в том, что X ( ; ) . Очевидно, что такое событие достоверно.
6
Геометрически свойство 2 означает, что площадь фигуры,
ограниченной осью Ox и кривой распределения равна единице. В частности,
если все возможные значения случайной величины X (a;b) , то имеет место
b
равенство f (x)dx 1.
a
11.3. Числовые характеристики непрерывных случайных величин
Математическим ожиданием непрерывной случайной величины X ,
возможные значения которой принадлежат отрезку a;b , называют
b
определенный интеграл M ( X ) xf (x)dx .
a
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ожидания.
Если возможные значения возможные значения случайной величины
X принадлежат отрезку a;b , |
b |
|
||
то D( X ) (x M ( X ))2 f (x)dx . Если возможные |
||||
|
|
|
a |
|
значения возможные значения случайной величины |
X принадлежат всей |
|||
|
|
|
|
|
числовой оси, то M ( X ) xf (x)dx и D( X ) (x M ( X ))2 |
f (x)dx . |
|||
|
|
|
|
|
Среднее квадратическое отклонение непрерывной случайной |
||||
величины определяется, как |
и для величины дискретной, равенством |
|||
|
|
|
|
|
( X ) D( X ) . |
|
|
||
Свойства математического ожидания и дисперсии сохраняются и для
непрерывных величин.
Легко получить для вычисления дисперсии более удобные формулы
b |
|
|
|
D( X ) x2 f (x)dx (M ( X ))2 |
и |
D( X ) x2 f (x)dx (M ( X ))2 , |
или |
a |
|
|
|
D(X ) M (X 2 ) (M (X ))2 . |
|
|
|
