
- •Липецкий государственный технический университет
- •1 Определение критериев подобия способом интегральных аналогов…..4
- •2 Определение критериев подобия на базе π-теоремы……………………...7
- •1 Определение критериев подобия способом интегральных аналогов.
- •1.1 В первой форме записи
- •1.2 Во второй форме записи
- •1.3 В третьей форме записи
- •2 Определение критериев подобия на базе π-теоремы
- •2.1 Составление матрицы размерностей параметров процесса
- •2.2 Определение независимых параметров процесса и числа возможных форм записи критериев подобия
- •2.3 Определение критериев подобия в трех формах записи
- •2.3.1 В первой форме записи
- •2.3.2 Во второй форме записи
- •2.3.3 В третьей форме записи
2.3 Определение критериев подобия в трех формах записи
2.3.1 В первой форме записи
Определим первую форму записи критериев подобия:
Найдем соотношения между независимыми и зависимыми параметрами, и они будут иметь следующий вид:
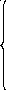 [
[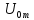 ]
=
]
=
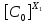
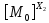
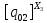
[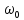 ]
=
]
=
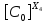
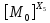
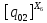
[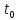 ]
=
]
=
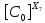
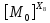
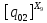 (2.5)
(2.5)
[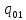 ]
=
]
=
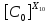
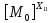
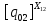
[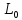 ]
=
]
=
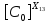
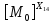
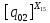
Следующая задача заключается в нахождении
показателей
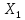 ,
,
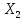 ,…,
,…,
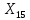 .
.
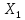 =
=
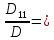
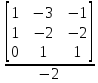 = -1;
= -1;
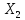 =
=
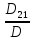 =
=
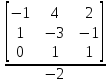 = 0
= 0
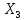 =
=
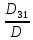 =
=
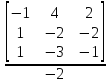 = 1 ;
= 1 ;
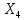 =
=
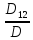 =
=
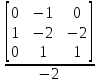 = -0.5
= -0.5
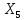 =
=
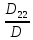 =
=
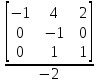 = -0.5;
= -0.5;
 =
=
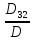 =
=
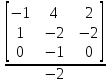 = 0
= 0
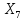 =
=
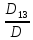 =
=
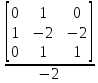 = 0.5 ;
= 0.5 ;
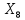 =
=
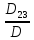 =
=
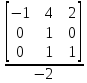 = 0.5
= 0.5
 =
=
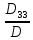 =
=
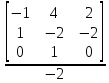 = 0;
= 0;
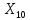 =
=
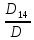 =
=
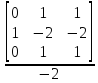 = 0
= 0
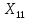 =
=
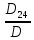 =
=
 = 0;
= 0;
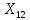 =
=
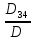 =
=
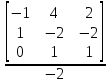 = 1
= 1
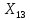 =
=
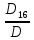 =
=
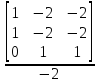 = 0 ;
= 0 ;
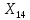 =
=
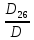 =
=
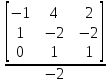 = 1
= 1
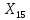 =
=
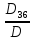 =
=
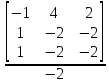 = 0
= 0
После подстановки найденных значений
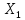 ,
,
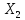 ,…,
,…,
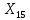 в систему (2.5), получаем:
в систему (2.5), получаем:
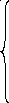 [
[ ]
=
]
=
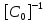

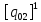
[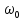 ]
=
]
=
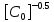
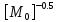
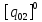
[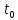 ]
=
]
=
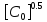
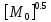
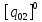 (2.66)
(2.66)
[ ]
=
]
=
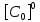
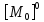
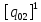
[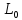 ]
=
]
=
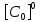
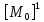
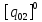
Учитывая, что связь между единицами измерения идентична связи между самим физическими величинами, мы можем записать следующее:
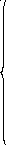
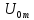 =
=
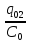
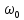 =
=
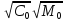
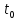 =
=
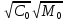 (2.7)
(2.7)
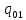 =
=
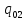
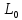 =
=
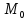
Так как
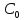 ,
,
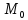 и
и
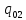 независимые величины, то мы можем выбрать
их произвольно. Выберем их таким образом:
независимые величины, то мы можем выбрать
их произвольно. Выберем их таким образом:
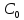 = С,
= С,
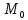 =
=
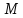 ,
,
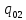 = q
= q
Подставляя выбранные значения в выражение (2.2) вместо входящих в него параметров, получим:
f ( ,
,
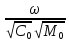 ,
,
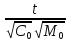 ,
,
 ,
,
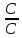 ,
,
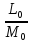 ,
,
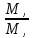 ,
,
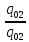 )
= 0
(2.8)
)
= 0
(2.8)
f (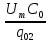 ,
,
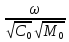 ,
,
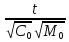 ,
,
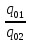 ,
1,
,
1,
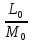 ,
,
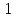 , 1,
) = 0 (2.9)
, 1,
) = 0 (2.9)
На основании первой теоремы подобия все отношения (отличные от единицы, входящие в выражение (2.9)) представляют собой критерии подобия в первой форме записи.
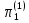 =
=
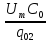 ,
,
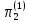 =
=
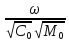 ,
,
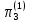 =
=
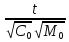 ,
,
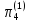 =
=
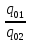 ,
,
,
,
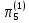 =
=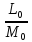 .
.
2.3.2 Во второй форме записи
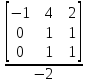
По аналогии с пунктом 2.3.1 определим вторую форму записи критериев подобия. Найдем определитель третьего порядка отличный от нуля и отличный от предыдущего хотя бы одной строкой.
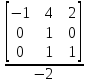
M T I



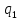 0 1 1
0 1 1
D = C -1 4 2 = -2
 M 1 -2 -1
M 1 -2 -1
В качестве независимых параметров во
второй форме записи будут являться
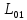 ,
,
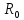 и
и
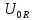 .
Остальные параметры будут зависимы и
будут выражаться через независимые.
Найдем соотношения между зависимыми и
независимыми параметрами, и они будут
иметь следующий вид:
.
Остальные параметры будут зависимы и
будут выражаться через независимые.
Найдем соотношения между зависимыми и
независимыми параметрами, и они будут
иметь следующий вид:
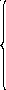 [
[ ]
=
]
=
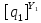
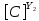
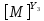
[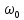 ]
=
]
=
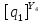
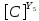
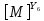
[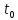 ]
=
]
=
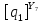
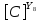
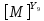 (2.10)
(2.10)
[L] =
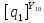
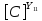
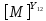
[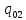 ]
=
]
=
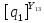
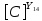
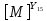
Следующая задача заключается в нахождении
показателей
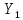 ,
,
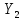 ,…,
,…,
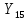 .
.
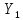 =
=
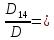
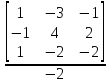 = 1;
= 1;
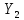 =
=
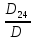 =
=
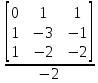 = -1
= -1
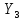 =
=
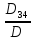 =
=
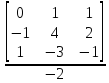 = 0;
= 0;
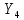 =
=
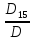 =
=
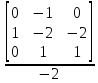 = 0.5
= 0.5
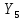 =
=
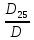 =
=
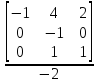 = -0.5;
= -0.5;
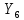 =
=
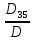 =
=
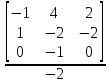 = 0
= 0
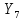 =
=
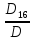 =
=
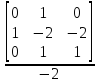 = 0.5;
= 0.5;
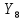 =
=
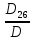 =
=
 = 0.5
= 0.5
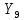 =
=
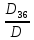 =
=
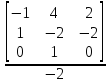 = 0;
= 0;
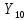 =
=
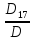 =
=
 = 0
= 0
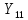 =
=
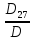 =
=
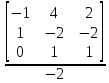 = 1;
= 1;
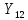 =
=
 =
=
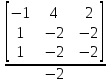 = 0
= 0
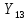 =
=
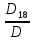 =
=
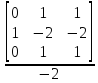 = 0;
= 0;
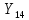 =
=
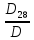 =
=
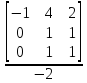 = 0
= 0
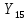 =
=
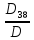 =
=
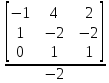 = 1
= 1
После подстановки найденных значений
 ,
,
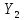 ,…,
,…,
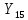 в систему (2.10), получаем:
в систему (2.10), получаем:
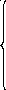 [
[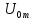 ]
=
]
=
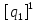
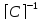
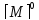
[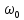 ]
=
]
=
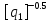
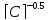
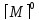
[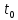 ]
=
]
=
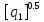
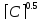
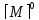 (2.11)
(2.11)
[L] =
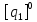
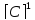
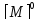
[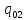 ]
=
]
=

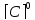
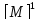
Учитывая, что связь между единицами измерения идентична связи между самим физическими величинами, мы можем записать следующее:
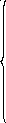
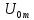 =
=
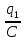
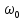 =
=
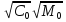
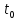 =
=
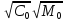 (2.12)
(2.12)
L =

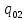 =
=
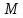
Так как
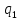 ,
,
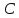 и
и
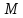 независимые величины, то мы можем выбрать
их произвольно. Выберем их таким образом:
независимые величины, то мы можем выбрать
их произвольно. Выберем их таким образом:
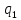 =
=
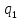 ,
,
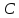 =
=
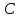 ,
,
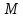 =
=
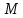
Подставляя выбранные значения в выражение (2.2) вместо входящих в него параметров, получим:
f (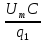 ,
,
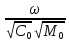 ,
,
 ,
,
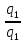 ,
,
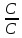 ,
,
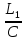 ,
,
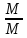 ,
,
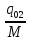 )
= 0
(2.13)
)
= 0
(2.13)
f ( ,
,
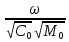 ,
,
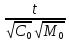 ,
,
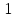
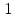 ,
,
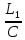 ,
,
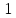 ,
,
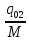 )
= 0 (2.14)
)
= 0 (2.14)
На основании первой теоремы подобия все отношения (отличные от единицы, входящие в выражение (2.14)) представляют собой критерии подобия во второй форме записи.
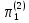 =
=
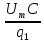 ,
,
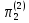 =
=
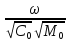 ,
,
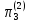 =
=
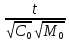 ,
,
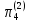 =
=
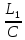 ,
,
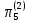 =
=
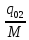 .
.
