
1. Напряженно-деформированное состояние толстостенной трубы в условиях упругой деформации
В случае плоской деформации можно
расположить цилиндрическую систему
координат так, что движение среды будет
происходить параллельно плоскостиx0y,
а все характеристики напряженно-деформируемого
состояния не будут зависеть от координаты
z:
случае плоской деформации можно
расположить цилиндрическую систему
координат так, что движение среды будет
происходить параллельно плоскостиx0y,
а все характеристики напряженно-деформируемого
состояния не будут зависеть от координаты
z:
![]() ; (1)
; (1)
![]() . (2)
. (2)
Внешние нагрузки приложены к трубе таким образом (см. рис.), что решение задачи будет инвариантным относительно поворотов на любой угол относительно оси z, т. е. напряженно-деформированное состояние является осесимметричным, и характеристики напряженно-деформированного состояния не зависят от координаты :
![]() ; (3)
; (3)
![]() . (4)
. (4)
Тензор напряжений в этом случае принимает вид
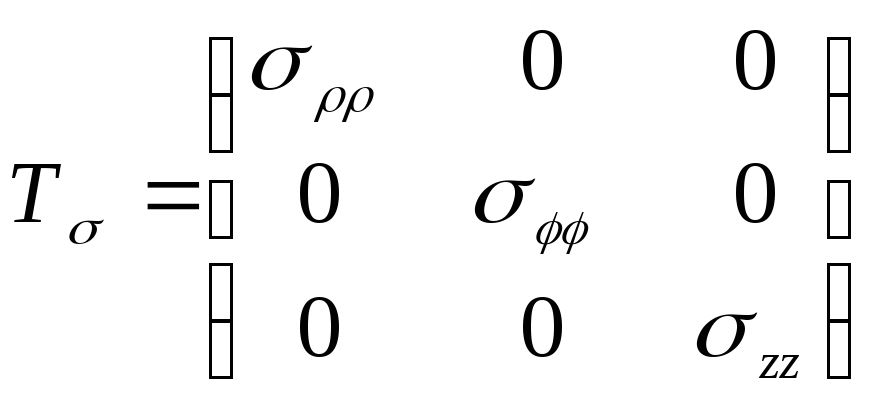 ,
(5)
,
(5)
где , , zz – главные нормальные напряжения. В дальнейшем будем обозначать их , , z.
Связь деформаций с перемещениями для плоского деформированного и осесимметричного состояния
![]() ;
;![]() ;
;![]() . (6)
. (6)
Таким образом, деформации , являются относительными удлинениями в направлении осей координат , . В дальнейшем будем обозначать их , .
Расчет напряженно-деформированного состояния тела заключается в определении компонент тензоров напряжений и деформаций в любой его точке, т.е. выражении напряжений и деформаций в виде функций координат. В случае плоского деформированного и осесимметричного состояния напряжения и деформации будут зависеть от координаты .
Связь нормальных напряжений и деформаций по осям координат определяется законом Гука с учетом температурных напряжений:
![]() ;
;
![]() ; (7)
; (7)
![]() ,
,
где G – модуль упругости второго рода
![]() ; (8)
; (8)
– постоянная Ламе
![]() ; (9)
; (9)
– относительное изменение объема
![]() ; (10)
; (10)
К – объемный модуль упругости (модуль объемного расширения)
![]() ; (11)
; (11)
![]() –модуль
Юнга;
–модуль
Юнга;
![]() – коэффициент Пуассона;
– коэффициент Пуассона;![]() – температурный коэффициент линейного
расширения;t
– функция, задающая температурное поле
в трубе.
– температурный коэффициент линейного
расширения;t
– функция, задающая температурное поле
в трубе.
Запишем 1-е уравнение равновесия для цилиндрической системы координат
![]() . (12)
. (12)
Для условий плоского деформированного состояния уравнения (7, 12) примут вид
![]() ,
,
![]() , (13)
, (13)
![]() ,
,
![]() . (14)
. (14)
Вычислив
производную
![]() по
уравнению (14) и подставив (6, 13) в (14),
получим:
по
уравнению (14) и подставив (6, 13) в (14),
получим:
 . (15)
. (15)
Приняв
во внимание, что
![]() и с учетом (8, 9, 11)
и с учетом (8, 9, 11)
![]() . (16)
. (16)
После интегрирования левой и правой частей уравнения (16)
![]() . (17)
. (17)
Выполнив
преобразование
![]() и проинтегрировав уравнение (17), получим
выражение для расчета перемещенийu
в зависимости от координаты
и проинтегрировав уравнение (17), получим
выражение для расчета перемещенийu
в зависимости от координаты
![]() , (18)
, (18)
где J – температурный функционал,
![]() . (19)
. (19)
Определим деформации (относительные удлинения по осям координат)
![]() ; (20)
; (20)
![]() . (21)
. (21)
Подставив (20, 21) в уравнения закона Гука (13), получим выражения для определения нормальных напряжений в зависимости от координаты :
 ; (22)
; (22)
 ; (23)
; (23)
![]() . (24)
. (24)
Постоянные
интегрирования
![]() и
и![]() находятся из граничных условий. Подставив
в формулу (22)
находятся из граничных условий. Подставив
в формулу (22)![]() и
и![]() ,
получим систему из двух уравнений с
двумя неизвестными:
,
получим систему из двух уравнений с
двумя неизвестными:
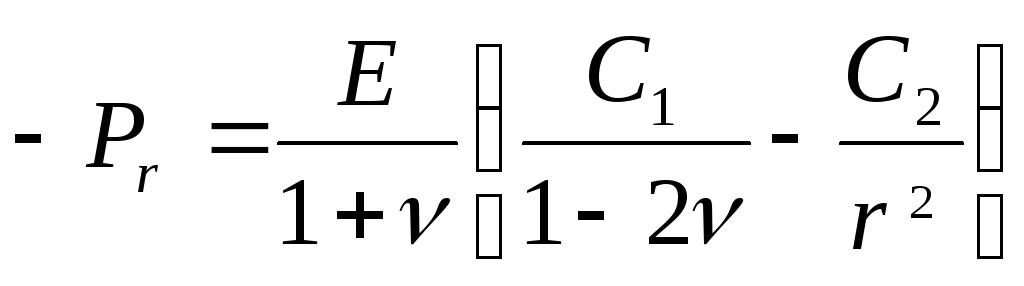 ; (25)
; (25)
 , (26)
, (26)
где ![]() . (27)
. (27)
Решая систему уравнений (25, 26), получим:
![]() , (28)
, (28)
![]() . (29)
. (29)
Температурный коэффициент линейного расширения определяется в процессе эксперимента по формуле
![]() , (30)
, (30)
где
![]() – длина тела при температуре
– длина тела при температуре![]() ;
;![]() – длина тела при температуре
– длина тела при температуре![]() ;
;![]() –
перепад температур.
–
перепад температур.
Из
формулы (30) следует, что при отсутствии
теплового расширения (![]() -
-![]() =
0) температурный коэффициент
=
0) температурный коэффициент![]() .
При этом в расчете напряженно-деформированного
состояния тела не учитываются напряжения
и деформации, вызванные температурным
полем. В этом случае расчетные формулы
(28, 29, 18, 20-24) примут следующий вид:
.
При этом в расчете напряженно-деформированного
состояния тела не учитываются напряжения
и деформации, вызванные температурным
полем. В этом случае расчетные формулы
(28, 29, 18, 20-24) примут следующий вид:
![]() ; (31)
; (31)
![]() ; (32)
; (32)
![]() ; (33)
; (33)
![]() ; (34)
; (34)
![]() ; (35)
; (35)
 ; (36)
; (36)
 ; (37)
; (37)
![]() . (38)
. (38)
При
отсутствии внешнего и внутреннего
давления, граничные условия принимают
вид
![]() и
и![]() .
В этом случае труба деформируется за
счет температурных напряжений. С учетом
новых условий выражения (28, 29) примут
следующий вид:
.
В этом случае труба деформируется за
счет температурных напряжений. С учетом
новых условий выражения (28, 29) примут
следующий вид:
![]() , (39)
, (39)
![]() . (40)
. (40)
Перемещение
![]() ,
деформации
,
деформации![]() ,
,![]() и напряжения
и напряжения![]() ,
,![]() ,
,![]() определяются по формулам (18-24) с учетом
(39, 40).
определяются по формулам (18-24) с учетом
(39, 40).
В общем случае интенсивность касательных напряжений T и интенсивность деформаций сдвига Г можно определить по формулам:
![]() ; (41)
; (41)
![]() . (42)
. (42)
После выполнения соответствующих преобразований (рекомендуется выполнить самостоятельно) придем к заключению, что напряжения и деформации в толстостенной трубе, нагруженной внутренним и внешним давлением, можно представить в виде суммы двух составляющих: напряжений и деформаций, вызванных присутствием температурного поля, и напряжений и деформаций, вызванных действием граничных условий.
![]() ; (43)
; (43)
![]() ; (44)
; (44)
![]() ; (45)
; (45)
![]() ; (46)
; (46)
![]() ; (47)
; (47)
![]() . (48)
. (48)
