
- •Основы Алгоритмизации и Программирования
- •Цели :
- •Литература
- •Методические пособия
- •Тема 1 Программирование с
- •Рекуррентные соотношения и стратегии решения задачи разбиением ее на подзадачи
- •• Определение 1.
- •Определение 2.
- ••Любое правильное рекуррентное уравнение при задании начального условия описывает некую счетную бесконечную последовательность
- •Примеры описания объектов с помощью рекуррентных уравнений
- •Примеры описания объектов с помощью рекуррентных уравнений
- •Примеры описания объектов с помощью рекуррентных уравнений
- ••Все выше приведенные определения являются рекурсивными, т.е. представляют объект соотношением, выражающим объект через
- ••В общем виде рекурсивный алгоритм P можно
- •Решать задачу рекурсивно (т.е. составить рекурсивный алгоритм)
- •Вычисление n-го числа Фиббоначи
- •Две стратегии разбиения на подзадачи
- •Стратегия
- •Недостаток стратегии РиВ
- •Стратегия
- •Суть стратегии ДП
- •Программирование рекуррентных соотношений
- •Вычисление n!
- •Найдем максимум a1...an
- •Нахождение max(a1..an) (как метод класса)
- •Нахождение max(a1..an)
- ••Итерация - от человека.
- •Класс c методом ввода массива
- •Найти max делением пополам
- •Найти номер max делением пополам
- •Работа с методами класса Tob
- •Замечание
- •Особенности выполнения рекурсивной подпрограммы
- •Особенности выполнения
- •Особенности выполнения
- •Рекурсивный вызов может быть прямым,
- •Организация выхода из рекурсии
- •Условия окончания рекурсии
- •О целесообразности использования рекурсивных подпрограмм
- •Неподходящий пример
- •Решение с помощью итерационного алгоритма по стратегии динамического программирования
- •рекомендация
- •Задача о Ханойской башне
- •Ханойская башня
- •Ханойская башня из 2 дисков
- •Ханойская башня из n дисков
- •Рекурсивный алгоритм
- •Рекурсивная подпрограмма
- •Hanoi(3,1,2,3) вызовет следующее дерево активаций и печати
- •результат
- •Три диска
- •Функция Аккермана
- •Матрица Аккермана
- •Рекурсивная функция
- ••procedure TForm1.Button1Click(Sender: TObject);
- •Правила выбора программной реализации рекуррентных соотношений
- •если возникающие подзадачи на каждом шаге независимы, то каждая из них будет решаться
- ••Контрольные вопросы
- •Задачи для контроля
- •Задачи для контроля
- •Конец темы 1
Ханойская башня из 2 дисков
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
02.07.19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
51 |
|

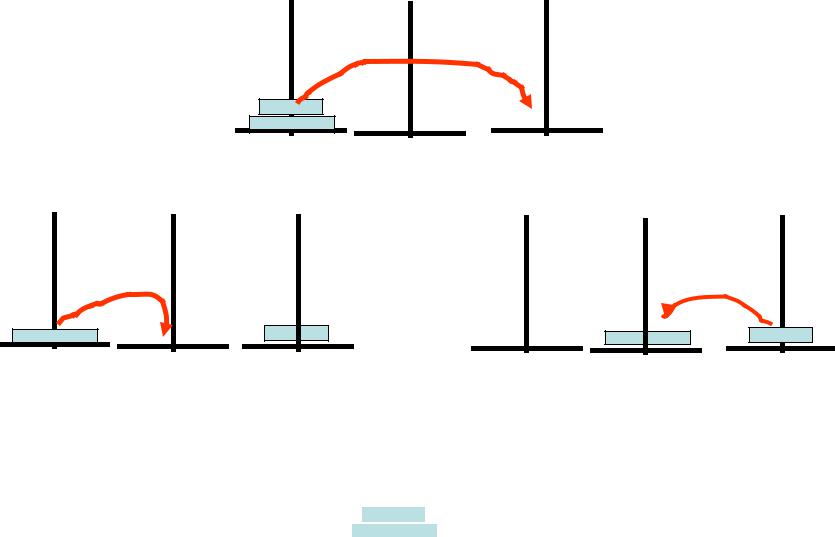
Ханойская башня из n дисков
Рекуррентное соотношение
Второй диск, состоит из n-1 дисков
Один диск
02.07.19 |
52 |
Рекурсивный алгоритм
•Тривиальная задача – башня из 1 диска, решается за один прием:
•1) перенести диск с s1 на s2.
•Элементарная подзадача – башня из двух дисков, решается в три приема:
•1) перенести диск с s1 на s3
•2) перенести диск с s1 на s2
•3) перенести диск с s3 на s2
•Рекурсивное соотношение:
•Башня из n дисков представляется как башня из 2-х – один нижний и верхний, состоящий из n-1 дисков.
02.07.19 |
53 |
Рекурсивная подпрограмма
•Procedure Hanoi(n,s1,s2,s3:word);
•Begin
•If n>0 then
•begin
• |
Hanoi(n-1,s1,s3,s2); |
• |
print(перенести диск со стержня s1 на стержень s2); |
• |
Hanoi(n-1,s3,s2,s1); |
• |
end; |
•end;
•Обращение: Hanoi(n,1,2,3).
02.07.19 |
54 |

Hanoi(3,1,2,3) вызовет следующее дерево активаций и печати
n=3, S1=1 S2=2 s3=3
2, 1 3 2 |
1->2 |
|
2, 3 2 1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, 1 2 3 |
1->3 |
1, 2 3 1 |
|
1, 3 1 2 |
3 ->2 |
1, 1 2 3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1->2 |
2->3 |
3->1 |
1->2 |
02.07.19 |
55 |
результат
•перенести диск со стержня 1 на стержень 2
•перенести диск со стержня 1 на стержень 3
•перенести диск со стержня 2 на стержень 3
•перенести диск со стержня 1 на стержень 2
•перенести диск со стержня 3 на стержень 1
•перенести диск со стержня 3 на стержень 2
•перенести диск со стержня 1 на стержень 2
02.07.19 |
56 |
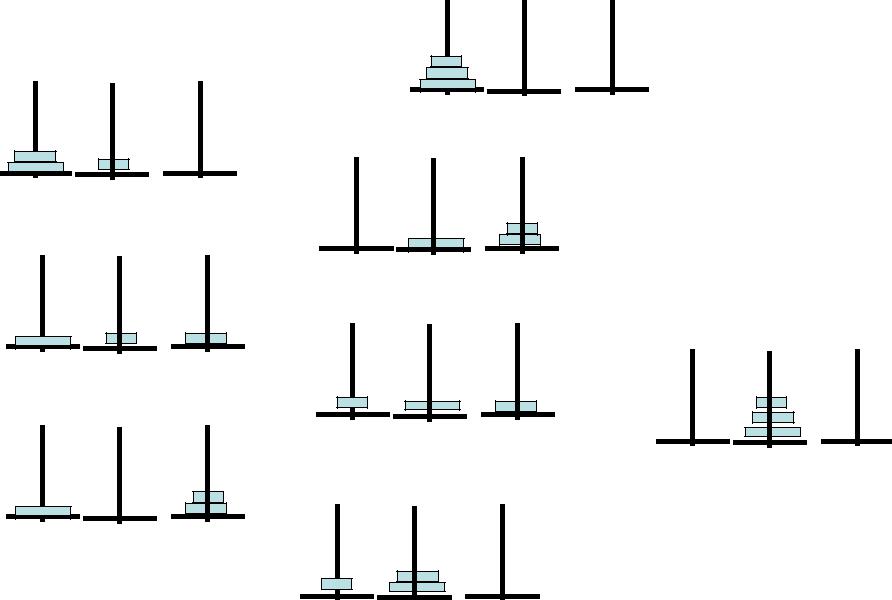
Три диска
1)
2) |
3) |
0)
4) |
5) |
7) |
|
6) |
02.07.19 |
57 |
Функция Аккермана
•A(0,n)=n+1
•A(m,0)=A(m-1,1), m>0
•A(m,n)=A(m-1,A(m,n-1)), m>0, n>0
02.07.19 |
58 |

Матрица Аккермана
02.07.19 |
59 |
Рекурсивная функция
•function ak(m,n:byte):cardinal;
•begin
•if m=0 then ak:=n+1
• |
else |
if (n=0) and (m>0) then ak:=ak(m-1,1) |
• |
else |
ak:=ak(m-1,ak(m,n-1)); |
•end;
02.07.19 |
60 |
