Получение алгебраической СЛАУ для искомых значений ui
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
ui-1 |
|
|
|
|
|
|
|
|
ui |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
f |
|
x,u |
|
; |
|
u(0) ; |
|
u(b) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ui+1 |
|
|
||||||||||||||||||||||||
x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
u |
|
|
|
|
|
|
ui 1 ui |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x |
|
|
i 1/ 2 |
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
ui ui 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
xi xi+1 b |
x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
i 1/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xi+1/2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xi-1/2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ui 1 ui |
|
ui ui 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ui 1 2ui ui 1 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
u |
|
|
|
|
i 1/ 2 |
|
i 1/ 2 |
|
|
h |
|
h |
|
|
|
|
|
|
|
|
fi |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x |
|
|
|
|
|
|
|
h |
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
x |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
07/02/19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
||||||
aiui 1 biui ciui 1 |
|
, |
i 2...n. |
|
|
, |
|
|
, |
fi |
u |
u |
n 1 |
||||||
|
|
|
|
1 |
|
|
|||
Получаем характерную для этих задач систему конечно-разностных уравнений
1 |
0 |
0 |
0 ... |
0 |
|
b2 |
c2 |
0 ... |
0 |
a2 |
||||
0 |
a3 |
b3 |
c3 ... |
0 |
|
|
|
|
|
... ... ... ... ... ... |
||||
0 |
0 |
0 |
0 ... |
an |
|
0 |
0 |
0 ... |
0 |
0 |
||||
00
00
00
... ...
bn cn
01
u1u2u3...
unun1
|
|
|
|
||
|
|
|
|
d |
|
2 |
||
|
d |
|
|
3 |
|
|
|
|
|
... |
|
|
||
|
|
|
|
dn |
|
|
||
|
|
|
|
07/02/19 |
12 |
При решении более сложных ДУ методом конечных элементов приходится решать СЛАУ
r r
Ax b
размерностью n=100 1000000
1 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
|
x |
|
b |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|||
|
2 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
0 |
|
x |
2 |
|
b |
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
||||
2 0 3 0 1 0 0 0 |
|
x3 |
b3 |
|
|||||||||
|
1 |
0 |
3 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
0 |
|
x |
4 |
|
b |
|
|||||||
|
|
|
|
|
|
|
|
|
4 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
3 |
0 |
1 |
0 |
|
|
|
||||
0 0 1 |
|
x5 |
|
b5 |
|
||||||||
|
0 |
0 |
1 |
0 |
3 |
0 |
1 |
|
|
|
|||
0 |
|
x |
|
b |
|
||||||||
|
|
|
|
|
|
|
|
|
6 |
6 |
|||
|
|
|
0 |
1 |
0 |
3 |
1 |
|
|
|
|
|
|
0 0 0 |
|
x7 |
|
b7 |
|
||||||||
|
0 |
0 |
0 |
1 |
1 |
0 |
2 |
|
|
|
|||
0 |
|
x |
|
b |
|
||||||||
|
|
|
|
|
|
|
|
|
8 |
8 |
|||
07/02/19 |
13 |
Прямой ход метода Гаусса приводит эту систему к СЛАУ с верхней треугольной матрицей
30000000
1 |
2 |
0 |
0 |
0 |
7 |
4 |
1 |
0 |
0 |
0 |
9 |
2 |
1 |
0 |
0 |
0 |
4 |
5 |
1 |
0 |
0 |
0 |
7 |
9 |
0 |
0 |
0 |
0 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
00
00
00
00
1 0
4 1
5 1
02
x1x2x3x4
x5x6x7x8
b1 b2
b3 b
4b5
b
6 b7
b8
Решается такая система начиная с последней строчки
07/02/19 |
14 |
Схема алгоритма
Метода Гаусса
С выбором главного элемента
07/02/19 |
15 |
Одним из рациональных способов хранения не нулевых элементов матрицы является
массив связанных списков a[i,j]
ms[1..m] Inf=(j,a)
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Inf |
A |
|
|
|
Inf |
A |
|
|
Inf |
nil |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
Inf |
A |
|
|
|
Inf |
nil |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m-1 |
|
|
|
Inf |
A |
|
|
|
Inf |
nil |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
Inf |
nil |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
07/02/19 |
|
|
|
|
|
|
|
|
|
|
16 |
|||||
Эффективность работы с таким массивом определяется введением класса с продуманным набором методов и создание на этой основе эффективных процедур работы с матрицами
Ниже мы приведем пример базового класса с набором методов, позволяющих вводить ненулевой элемент, распечатать матрицу, реализовать метод Гаусса решения СЛАУ
При реализации других методов работы с матрицами (умножение, сложение, нахождение обратной матрицы, …) может возникнуть необходимость в дополнительных методах базового класса.
07/02/19 |
17 |
Тип ячеек массива
•Unit URazMat
•Interface
•Type
•Tinf=record
• |
a:extended; |
// элемент и номер столбца |
• |
j:word; |
|
• |
end; |
|
• |
//ячейка с косвенной адресацией |
|
•Tsel=^sel;
•sel=record
•inf:Tinf;
•A:Tsel;
•end;
07/02/19 |
18 |
Методы работы со стеком, которые в дальнейшем понадобятся для реализации метода Гаусса
•Tlists=class(Tobject)
•sp1,sp:Tsel;
• |
//добавить в начало стека |
• procedure adds(inf:Tinf); |
|
• |
// добавить с упорядочением по j |
• Procedure addsj(inf:tinf); |
|
• |
// читать j-й элемент |
• function readsj(j:word):extended; |
|
• |
// удаление первого элемента |
•procedure dels;
•end;
07/02/19 |
19 |
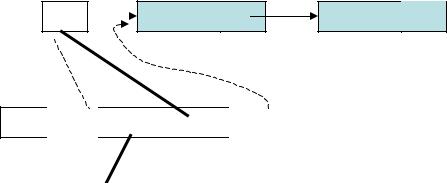
Методы работы со стеком Добавить элемент в начало стека
•Procedure TLists.Adds(Inf:Tinf);
•begin
• New(sp);
• sp^.Inf:=Inf;
• sp^.A:=sp1;
• |
|
sp1:=sp; |
|
• |
end; |
sp1 |
|
|
|
|
|
sp 
07/02/19 |
Inf |
20 |
|