Использование модуля «Solver» в OpenOffice.org Calc

©Иван Хахаев, 2008

В современных коммерческих офисных пакетах имеется модуль электронной таблицы (ЭТ), называемый «Solver» (или «Поиск решения»), который используется для решения задач, относящихся к классу «линейной оптимизации».

Однако в свободном офисном пакете OpenOffice.org начиная с версии 2.3 такой модуль также имеется (либо как расширение, устанавливаемое пользователями дополнительно, либо прямо в составе сборки пакета). Таким образом, решение задач линейной оптимизации вполне возможно и с использованием свободно распространяемых офисных пакетов (аналогичный модуль есть в составе свободной электронной таблицы Gnumeric).

Задача линейной оптимизации.

Для разбора предлагается задача, взятая из учебного пособия «Математическое программирование», авторы Э.Ф.Брыжина и Э.А.Худобина, издательство СПбГИЭА, 1997 год.

Задача: Имеется три вида сырья в количествах 45 ед., 19 ед. и 10 ед. Из этого сырья нужно изготовить продукцию двух видов. Задан расход сырья каждого вида на производство единицы каждого вида продукции и прибыть от единицы продукции (см. таблицу). Требуется найти такой вариант выпуска каждого вида продукции, при котором прибыль будет наибольшей.

Таблица исходных данных для задачи.

Продукция	Продукт 1	Продукт 2	Запасы сырья
Сырье
1	5	9	45
2	3	3	19
3	2	1	10
ПРИБЫЛЬ	5	6

(Далее – абзац по тексту источника) Обозначим через x₁ количество единиц продукции первого вида, через x₂ – второго вида. Тогда на выпуск этой продукции будет израсходовано 5x₁ +9x₂ ед. сырья первого вида, 3x₁ +3x₂ ед сырья второго вида и 2x₁ +x₂ - третьего. Суммарная прибыль составит 5x₁ +6x₂ денежных единиц. Т.к. нельзя израсходовать сырья больше, чем имеется, а суммарная прибыль зависит от количества выпущенной продукции, то получим следующую математическую модель данной задачи.

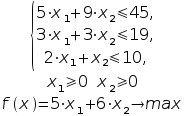
Решение задачи с использованием модуля «Solver».

Для решения задачи в ЭТ прежде всего нужно определиться с расположением исходных данных и составить необходимые формулы. Пусть таблица будет скомпонована в соответствии с рис. 1.

Рисунок 1. Исходные данные и формулы для поиска решения

Количества продукции 1-го и 2-го вида (которые предстоит вычислить) располагаются в ячейках A3 и B3 соответственно. В C3 – формула для вычисления прибыли, в B6:B8 – формулы для левых частей ограничений (см. математическую модель). Соответствующие формулы, реализующие математическую модель, показаны на сером фоне справа от ячеек, в которые они должны быть записаны. Когда решение будет найдено, нули в ячейках ЭТ и пустые ячейки для параметров модели будут заменены какими-то другими значениями.

Вызов модуля «Solver» обеспечивается пунктом главного меню «Данные» (рис. 2).

Рисунок 2. Меню «Данные» пакета OpenOffice.org Calc

При выборе пункта «Solver» открывается диалог настройки поиска решения (рис. 3).

Рисунок 3. Диалог настройки поиска решения

В диалоге настройки поиска решения несколько полей ввода, и в них потребуется устанавливать адреса ячеек. Для поля «Целевая функция» требуется указать адрес ячейки, содержащей формулу для расчёта прибыли f(x) (в рассматриваемом примере — ячейка C3). Адрес можно ввести прямо в поле ввода, а можно нажать на кнопку сворачивания диалога справа от поля ввода и в получившуюся строку ввода (рис. 4) ввести адрес ячейки «методом указания», то есть щёлкнув левой кнопкой мыши по нужной ячейке (рис. 5).

Рисунок 4. Строка ввода для указания адреса ячейки или диапазона

Рисунок 5. Адрес указан выбором ячейки мышью

Для восстановления вида диалога снова воспользуемся кнопкой права от строки ввода.

Поскольку требуется найти максимум прибыли, переключатель «Цель» должен быть установлен в позицию «Максимум».

В поле ввода «Параметры функции» требуется указать ячейки, в которых должны вычисляться параметры (в нашем случае x₁ и x_2, то есть диапазон A3:B3). для заполнения этой строки опять используем соответствующую кнопку сворачивания диалога и метод указания, только теперь для выбора ячеек выделим нужный диапазон (рис. 6).

Рисунок 6. Выбор диапазона ячеек с параметрами целевой функции

Кнопка «Настройки» в диалоге позволяет ввести дополнительные ограничения модели (рис. 7).

Рисунок 7. Дополнительные ограничения модели

По самой природе рассматриваемой задачи должен быть включён режим «Линейная модель». Кроме того, в математической модели указано, что значения параметров должны быть неотрицательными (т.к. количество продукции не может быть отрицательным), поэтому включаем ещё и режим «Только положительные значения».

Далее, нужно добавить ограничения. Для этого нажимаем на кнопку «Добавить» и в появившемся мини-диалоге (рис. 8) определяем левую и правую части, а также вид (знак) ограничения.

Рисунок 8. Диалог добавления ограничения

В левой части каждого ограничения должен быть адрес одной ячейки (в которой записана формула для ограничения), а в правой части может быть как адрес ячейки, так и число (значение для ограничения), как, например, на рис. 9. В нашем случае для всех ограничений нужно устанавливать знак «не меньше» (<=), хотя возможны варианты «не больше» (>=) и «равно» (=). Для ввода адресов ячеек в левую часть ограничения тоже можно использовать «метод указания».

Рисунок 9. Ограничение с числом в правой части

Последовательно добавим все три ограничения и получим заполненный диалог настройки поиска решения (рис. 10).

Рисунок 10. Настройка поиска решения завершена

Нажатие на кнопку «Решить» приводит к появлению сообщения об успешно найденном решении (рис. 11), а в электронной таблице появляются значения параметров, целевой функции и ограничений, соответствующие найденному решению (рис. 12).

Рисунок 11. Сообщение об успехе

Рисунок 12. Результаты работы модуля «Solver»

Нужно отметить, что результаты полностью соответствуют приведённым в первоисточнике значениям 3 и 10/3.