41. Определение предела функции в точке по Коши.

Определение предела функции в точке a по Коши. Пусть f(x) определена на множестве X, и a - предельная точка X. Число b называется пределом f(x) при x  a, если для   > 0   > 0 такое, что для  x  {0 < x - a< }: f(x) - b < .

41. Определение предела функции f(x) при x по Коши.

Определение. Число А называется пределом функции f(x) при x , если для  > 0 B() > 0: x такого, что x > B

41. Определение неограниченной в точке функции.

41. Определение бесконечно малой функции в точке.

Определение. Функция f(x) называется бесконечно малой в точке x = a (при x  a), если

f(x)= 0.

Эквивалентное определение. f(x) называется бесконечно малой в точке a, если

  > 0   > 0,  x  {0 < | x - a | <  }: | f(x) | < .

41. Определение бесконечно большой функции в точке.

Определение. Функция f(x) называется бесконечно большой в точке x = a (при x  a), если

 A > 0   > 0,  x  {0 < | x - a | <  }: | f(x) | > A.

Обозначение: f(x) = .

41. Определение непрерывной функции в точке.

Определение 1. Пусть f(x) определена в некоторой окрестности точки а. f(x) называется непрерывной в точке а если f(x) = f(а)

Определение 2. f(x) называется непрерывной в точке а, если   > 0   > 0: | f(x) - f(а) | <  при | х - а | < .

41. Классификация точек разрыва функции.

Определение. Предельные точки области определения функции, в которых эта функция не является непрерывной, называются точками её разрыва.

1). Устранимый разрыв. Точка а называется точкой устранимого разрыва функции f(x), если  f(x), но f(x)  f(a) , либо в точке а функция f(x) вообще не определена.

2). Разрыв 1-го рода. Точка a называется точкой разрыва 1-го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу правое и левое предельные значения:

или

3). Разрыв 2-го рода. Точка a называется точкой разрыва 2-го рода, если в этой точке функция f(x) не имеет по крайней мере одного из односторонних предельных значений или если хотя бы одно из них бесконечно.

41. Определение точной верхней грани функции.

(Я, на всякий случай, привожу определения и верхней, и нижней граней)

Определение 1. Пусть f(x)- ограниченна сверху (снизу) на X, то есть  M (m) ,  x  X: f(x)  M (f(x)  m) . Число М (m) называется верхней (нижней) гранью функции f(x) на множестве Х. Наименьшая (наибольшая) из верхних (нижних) граней ограниченной сверху (снизу) на X f(x) называется её точной верхней (точной нижней) гранью и обозначается f(x) ( f(x)).

Эквивалентное определение. Число M (число m) называется точной верхней (точной нижней) гранью функции f(x) на множестве X, если выполнены следующие два требования: 1) для  x  X: f(x)  M (f(x)  m), 2) для   > 0 x  X, для которого справедливо неравенство

()

41. Определение производной функции в точке.

Определение. Производной функции f(x) в данной фиксированной точке x называется предел при x 0 разностного отношения (при условии, что этот предел существует).

41. Определение дифференцируемости функции.

Определение. Функция f(x) называется дифференцируемой в данной точке x , если приращение y этой функции в точке x, соответствующее приращению аргумента x, может быть представлено в виде

,

где A – некоторое число, не зависящее от x, а  - функция аргумента x, являющаяся бесконечно малой при x  0.

Т.к. произведение двух бесконечно малых x является бесконечно малой более высокого порядка, чем x, то можно определение переписать

(А = f’(x)).

41. Определение дифференциала функции.

Определение. Дифференциалом функции в точке x, соответствующим приращению аргумента x, называют главную линейную относительно x часть приращения этой функции в точке x.

Принято обозначать дифференциал функции символом dy,

.

Дифференциалом независимой переменной х называется приращение этой переменной: dx = x. Таким образом, dy = f '(x)dx, или

41. Определение производной вектор-функции.

Если каждому числу t из некоторого множества T поставлен в соответствие вектор, то говорят, что на множестве T, определена векторная функция (или вектор - функция) и пишут: =(t), t  T. |(t) | - скалярная функция.

Определение. Векторназывается пределом вектор-функции =(t) при t  t₀ если |(t) -|  0 при t t₀, (t) =.

Зафиксируем какое-нибудь значение t, а затем дадим приращение t  0 аргументу t. = (t + t) - (t)

Определение производной вектор-функции. Если существует , то он называется производной вектор-функции в точке t и обозначается '(t).

41. Определение предела последовательности.

Определение. Число А называется пределом последовательности , если для

  n>N x_n - A < 

Обозначение: .

41. Определение бесконечно большой последовательности.

Определение. Последовательность называется бесконечно большой, если для А > 0 N: n  N x_n > A.

41. Определение неограниченной последовательности.

Определение. Последовательность {x_n} называется неограниченной, если  A > 0  n: x_n > A.

41. Определение фундаментальной последовательности.

Определение. Последовательность {x_n} называется фундаментальной, если для   > 0  N:  n >N и  натурального p: x_n+p-x_n < .

41. Определение предельной точки числовой последовательности.

Определение 1. Число a называется предельной точкой последовательности {x_n}, если из последовательности {x_n} можно выделить подпоследовательность, сходящуюся к a.

Определение 2. Число a называется предельной точкой последовательности {x_n}, если в любой -окрестности точки a содержится бесконечно много членов последовательности {x_n}.

41. Определение предела функции в точке по Гейне.

Определение предела функции в точке a по Гейне. Число b называется пределом f(x) при x  a, если для  {x_n}  a (x_n  a): {f(x_n)}  b.

41. Определение предела функции f(x) при x по Гейне.

Определение (по Гейне). Число b называется пределом f(x) при x  +, если  {x_n}  +: {f(x_n)}  b.

41. Определение первообразной и неопределенного интеграла.

Определение 1. Функция F(x) называется первообразной для функции f(x) на X, если  xX: F'(x) = f(x).

Определение 2. Множество всех первообразных для функции f(x) на промежутке X называется неопределенным интегралом от этой функции на промежутке X и обозначается

.

f(x) называется подынтегральной функцией.

f(x)dx называется подынтегральным выражением.

41. Определение равномерно непрерывной функции.

Определение. Функция f(x) называется равномерно непрерывной на множестве {x}, если для   > 0 () > 0 такое, что для любых двух точек x’ и x’’ множества {x}, удовлетворяющих условию выполняется условие .

Примеры: - равномерно непрерывна на полупрямой x  1,

- не является равномерно непрерывной на множестве x  1,

не является равномерно непрерывной на интервале (0, 1).

41. Определение точки локального экстремума функции.

Определение. Пусть функция f(x) определена всюду в некоторой окрестности точки с. Говорят, что функция f(x) имеет в точке с локальный максимум (минимум), если существует такая окрестность точки с, в пределах которой значение f(с) является наибольшим (наименьшим).

Локальный максимум и минимум объединяются общим названием экстремум.

41. Определение наклонной асимптоты к графику функции.

Определение. Говорят, что прямая

(1)

является наклонной асимптотой графика функции при , если функция f(x) представима в виде

, где (2)

___________________________________________________________________________________

Определение. Говорят, что прямая x = a является вертикальной асимптотой графика функции , если хотя бы одно из предельных значений

или

равно + или -.

41. Определение точки перегиба графика функции.

Определение. Точка графика функции называется точкой перегиба этого графика, если существует такая окрестность точки с оси абсцисс, в пределах которой график функции слева и справа от с имеет разные направления выпуклости. (см. рисунок).

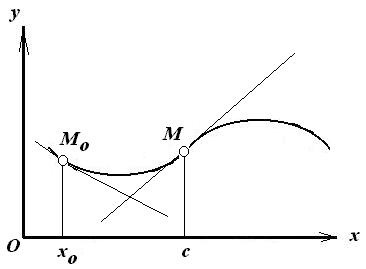
Иногда при определении точки перегиба графика функции дополнительно требуют, чтобы этот график всюду в пределах достаточно малой окрестности точки с оси абсцисс слева и справа от с лежал по разные стороны от касательной к этому графику в точке .

41. Определение направления выпуклости графика функции.

Предположим, что функция f(x) дифференцируема в любой точке интервала . Тогда существует касательная к графику функции , проходящая через любую точку этого графика , причем эта касательная не параллельна оси Oy.

Определение. График функции имеет на интервале выпуклость, направленную вниз (вверх), если график этой функции в пределах указанного интервала лежит не ниже (не выше) любой своей касательной.

41. Определение условно сходящегося ряда.

Определение. Ряд называется условно сходящимся, если этот ряд сходится , а соответствующий ряд из модулей расходится.

41. Определение абсолютно сходящегося ряда.

Определение. Ряд называется абсолютно сходящимся, если сходится ряд .