33. Направление выпуклости и точки перегиба графика функции.

1). Предположим, что функция f(x) дифференцируема в любой точке интервала . Тогдасуществует касательная к графику функции , проходящая через любую точкуэтого графика, причем эта касательная не параллельна оси Oy.

Определение.График функции имеет на интервале выпуклость, направленную вниз (вверх), если график этой функции в пределах указанного интервала лежит не ниже (не выше) любой своей касательной.

Теорема 9.4.Если функция имеет на интервале конечную вторую производную и если эта производная неотрицательна (неположительна) всюду на этом интервале, то график функции имеет на интервале выпуклость, направленную вниз (вверх).

Доказательство.Рассмотрим случай всюду на . Пустьс – любая точка интервала (рисунок). Требуется доказать, что график функции лежит не ниже касательной, проходящей

через точку . Запишем уравнение касательной, обозначая ее ординату через Y. Т. к. угловой коэффициент касательной равенf’(c), то

(1)

Разложим f(x) в окрестности точки с по формуле Тейлора до n = 1. Получим

(2)

где остаточный член взят в форме Лагранжа, лежит междуc иx. Поскольку по условиюf(x) имеет вторую производную на интервале , формула (2) справедлива длялюбого xиз этого интервала. Сопоставляя (2) и (1), имеем

(3)

Поскольку вторая производная по условию 0 всюду на , то правая часть (3)неотрицательна, т.е. для всех xиз или. Это неравенство доказывает, что график всюду в пределах интервала лежит не ниже касательной (1).

Аналогично доказывается теорема для случая .

Теорема доказана.

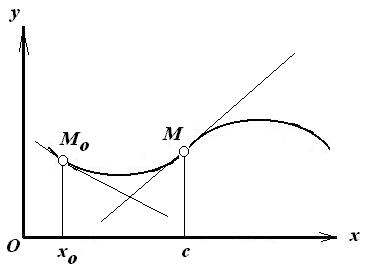
2). Точки перегиба графика функции.

Определение. Точка графика функции называется точкой перегиба этого графика, если существует такая окрестность точки с оси абсцисс, в пределах которой график функции слева и справа от с имеет разные направления выпуклости. (см. рисунок).

Иногда при определении точки перегиба графика функции дополнительно требуют, чтобы этот график всюду в пределах достаточно малой окрестности точки с оси абсцисс слева и справа от с лежал по разные стороны от касательной к этому графику в точке .

33. Необходимое условие перегиба графика функции.

Определение. Точка графика функции называется точкой перегиба этого графика, если существует такая окрестность точки с оси абсцисс, в пределах которой график функции слева и справа от с имеет разные направления выпуклости. (см. рисунок).

Иногда при определении точки перегиба графика функции дополнительно требуют, чтобы этот график всюду в пределах достаточно малой окрестности точки с оси абсцисс слева и справа от с лежал по разные стороны от касательной к этому графику в точке .

Лемма 1.Пусть функция имеет производную f’(x) всюду в -окрестности точки с, причем эта производная непрерывна в точке с. Тогда, если график имеет на интервале выпуклость, направленную вниз (вверх), то всюду в пределах интервалаэтот график лежит не ниже (не выше) касательной, проведенной в точке.

Доказательство. Рассмотрим последовательность точек интервала, сходящуюся к точкес. Через каждую точку графика проведем касательную к этому графику, т.е. прямую

Т.к. по условию имеет на интервале выпуклость, напрвленную вниз (вверх), то для любогоnи любойфиксированной точкиxинтервала

( 0) (1)

Из непрерывности f’(x) в точке с следует, что существует предел

(2)

Из (2) и (1) следует, что

( 0) (3)

Если обозначить через Yтекущую ординату касательной, проходящей через точку , то (3) можно переписать в виде

( 0) (4)

Переходя в неравенстве (1) к пределу при получим, что

( 0) (5)

для любой фиксированной точки xиз интервала .

Лемма доказана.