
Министерство образования Республики Беларусь Учреждение образования
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра высшей математики
А.А. Карпук, Р.М. Жевняк
Сборник задач по высшей математике
В10 частях Часть 1
Аналитическая геометрия
Минск БГУИР 2002

Введение
В настоящее время вузы получили самостоятельность в создании собственных учебных и типовых программ по курсу высшей математики. Поэтому существовавшие до 1991 г. сборники задач по высшей математике многие вузы уже не устраивают. Отсюда и появление в высших учебных заведениях большого количества методических пособий, в том числе и сборников задач, по различным разделам курса высшей математики.
Структура настоящего сборника задач следующая. Каждый пункт раздела предваряют теоретические сведения по изучаемому в нем объекту аналитической геометрии. Затем в качестве образца решается достаточное количество задач, поясняющих теорию. Знак ∆ означает начало решения задачи, а знак ▲- конец решения. В конце каждого пункта приводятся задачи для решения в аудитории и для домашнего задания. Наиболее сложные задачи отмечены звез-
дочкой (*). Все задачи снабжены в конце сборника ответами. Обозначения a,
M0 M и т.д. понимаются как векторы.

1.ВЕКТОРНАЯ АЛГЕБРА
1.1.Векторы. Линейные операции над векторами. Проекция вектора на ось. Линейно зависимые и линейно независимые векторы. Базис пространства. Координаты вектора в базисе.
Геометрическим вектором называется направленный отрезок АВ с на-
чальной точкой А и конечной точкой В (рис. 1.1). Обозначается: AB. Если
|
B |
отрезок АВ соответствует вектору a , то |
||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
(рис. 1.2). Вектор |
|
|
|
называет- |
|||||
|
ся |
пишут |
a |
|
AB |
BA |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
противоположным вектору |
|
|
. |
|
|
|
|
|
||||||||||||||
A |
B |
AB |
|
|
|
|
|
|||||||||||||||||
Рис. 1.1 |
Вектор |
AA |
|
называется нулевым |
и обозначается |
|||||||||||||||||||
a |
|
|
0 |
. Длиной |
|
|
AB |
|
вектора |
AB |
|
|
|
|
|
|
||||||||
A Рис. 1.2 |
|
или его модулем называется длина |
|
AB |
|
|
||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
соответствующего направленного отрезка. Вектор a0 , для которого a0 =1,
называется единичным. Векторы, параллельные одной и той же прямой или лежащие на ней, называются коллинеарными. Коллинеарность векторов обозна-
чается a // b .
Если векторы a и b коллинеарны и одинаково направлены (сонаправле-
ны), то этот факт обозначается в виде a ↑↑ b .
Если же коллинеарные векторы противоположно направлены, то это обозначается в виде a ↑↓ b . Векторы, параллельные одной и той же плоскости или лежащие в ней, называются компланарными. Векторы a и b называются равными, если они одинаково направлены и a = b .
Сложение векторов a и b осуществляется по правилу треугольника (рис. 1.3) или по правилу параллелограмма (рис. 1.4).
|
|
a |
|
|
|
a |
b |
a + b |
|
a |
a - b |
|
|
|
|||
|
|
|
b |
|
b |
|
|
|
|
|
|
Рис.1.3 |
|
Рис.1.4 |
|
|
Рис.1.5 |
4
Разность векторов a и b есть вектор a - b , изображенный на рис. 1.5.
Вектор a - b направлен к концу «уменьшаемого» вектора a .
Произведением вектора a на действительное число α называется вектор b =αa , длина которого b = α a , а направление b совпадает с направлени-
ем a при α > 0 и противоположно a , если α < 0. Если α ≠ 0 , то равенство b =αa является признаком коллинеарности векторов a и b .
|
|
≠ |
|
, то единичный вектор |
|
0 = |
|
1 |
|
|
|
|
|
|||
Если |
a |
0 |
a |
a |
называется ортом вектора |
|||||||||||
|
|
|
|
|
||||||||||||
a |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a .
Сложение векторов и умножение вектора на действительное число называются линейными операциями над векторами.
Углом между двумя векторами (или между вектором и осью) называется наименьший угол ϕ , 0 ≤ϕ ≤π , на которой нужно повернуть один вектор
(ось), чтобы он совпал по направлению с другим вектором (осью) (рис. 1.6). Обозначается : ϕ = (a,^ b) .
ϕ |
ϕ |
|
Рис. 1.6
Если ϕ =π / 2, то векторы a и b называются перпендикулярными или ортогональными.
Проекцией вектора a = AB на ось L (обозначается: прL a ) называется
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
длина |
направленного отрезка A1B1 , |
заключенного |
между |
ортогональными |
|||||||||||||||
проекциями начала и конца вектора |
AB |
на эту ось, |
причем |
прL |
a |
> 0, если |
|||||||||||||
|
|
|
и L одинаково направлены, и прL |
|
< 0 , если они противоположно на- |
||||||||||||||
|
A1B1 |
a |
|||||||||||||||||
правлены (рис. 1.7). Для проекции справедлива формула |
|
|
|
||||||||||||||||
|
|
|
прL |
|
= |
|
|
|
cosϕ. |
|
|
|
|
|
|
|
|
||
|
|
|
a |
a |
|
|
|
|
|
(1.1). |
|||||||||
Проекция вектора на ось обладает свойствами:
|
|
10. |
прL ( |
|
|
+ |
|
|
|
) =прL |
|
|
+ прL |
|
|
||||||||
a |
B |
a |
b |
a |
b |
||||||||||||||||||
20. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
прL (αa) =αпрL a, |
α R . |
||||||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
Векторы |
|
1, |
|
2 , |
|
3 из R3 |
|
||||||||||||||
A1 |
B1 L |
a |
a |
a |
называются ли- |
||||||||||||||||||
|
|
нейно зависимыми, если существуют числа |
|||||||||||||||||||||
5

Рис. 1.7 |
|
|
α1,α2 ,α3 R , |
не все равные нулю, |
такие, что |
||||
выполнено равенство |
|
|
1 +α2 |
|
2 +α3a3 = |
|
|
|
|
|
α1 |
|
|
|
|
|
|||
|
a |
a |
0. |
(1.2) |
|||||
Если же равенство (1.2) имеет место лишь при |
α1 =α2 =α3 = 0,то |
векторы |
|||||||
a1, a2 , a3 называются линейно независимыми.
Линейная зависимость векторов означает, что какой-то один из векторов,
например a3 , может быть представлен в виде линейной комбинации остальных, т.е.
|
3 = β1 |
|
1 + β2 |
|
2 , β1, β2 R . |
|
a |
a |
a |
(1.3) |
равенство (1.3) является признаком компланарности векторов a1, a2 , a3 . Любые два линейно независимых (неколлинеарных) вектора на плоскости
(в R2 ) образуют базис. Аналогично, любые три линейно независимых (некомпланарных) вектора в пространстве (в R3 ) также образуют базис. На прямой (в R1) базисом является любой ненулевой вектор, коллинеарный этой прямой.
Если векторы a1, a2 образуют базис на плоскости, то числа β1 и β2 в ра-
венстве (1.3) называются координатами (компонентами) вектора a3 в этом ба-
зисе. Этот факт записывается в виде |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a3 = β |
|
|
|
|
1 + β |
|
|
|
2 = (β , β |
|
|
) . |
|
|
(1.4) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
a |
2 |
a |
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
|
|
|
Если векторы |
|
1, |
|
|
2 , |
|
3 образуют базис в пространстве |
R3 , то всякий |
||||||||||||||||||||||||||||||||||
a |
a |
a |
|||||||||||||||||||||||||||||||||||||||||||
вектор |
|
|
|
|
4 R3 может быть представлен единственным образом в виде |
||||||||||||||||||||||||||||||||||||||||
a |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 = β |
|
|
1 |
+ β |
|
|
|
2 |
+ β |
|
|
|
3 |
|
= (β , β |
|
, β |
|
|
). |
|
|
(1.5) |
|||||||||||||||
a |
1 |
a |
2 |
a |
3 |
a |
|
2 |
3 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
4 в базисе векторов |
|||||||||
Числа β , β |
|
, β |
|
называются координатами вектора |
|
||||||||||||||||||||||||||||||||||||||||
2 |
3 |
a |
|||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1, |
|
2 , |
|
3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a |
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Если в декартовой системе координат (ДСК) (в базисе из единичных век-
|
|
|
|
|
|
|
|
) задан вектор |
|
= (x, y, z) = x |
|
+ y |
|
+ z |
|
, то его длина |
|||||||
торов |
i, |
|
j, |
|
|
k |
a |
i |
j |
k |
|||||||||||||
|
|
|
|
|
|
|
|
a = |
x2 + y2 + z2 . |
|
|
|
(1.6) |
||||||||||
Для орта |
|
0 вектора |
|
|
имеем |
|
|
|
|
|
|
|
|
|
|
||||||||
a |
a |
|
|
|
|
|
|
|
|
|
|
||||||||||||
a0 = 1 |
|
|
|
|
|
|
|
|
|
, |
y , |
|
|
|
(1.7) |
||||||||
a = 1 (x, y, z) = x |
|
z . |
|||||||||||||||||||||
|
|
|
a |
|
|
|
a |
|
|
a |
|
a |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|||||||||
6

|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
y |
, z |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Числа |
, |
|
называются |
|||||||||||||||||||||
|
|
|
γ |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
a |
a |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
направляющими косинусами вектора |
|
и |
||||||||||||||||||||||||||||||
|
|
k |
|
β |
|
|
|
|
|
|
|
|
|
|
Y |
a |
||||||||||||||||||||||||||||||||||||||
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обозначаются |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
i |
α j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
cosα = |
|
x |
|
|
, |
cos β = |
|
|
|
y |
|
|
|
, |
|
cosγ = |
|
|
|
z |
|
|
|
|
, |
|
|
|
|
|
(1.8) |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
a |
a |
a |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
cos2 α + cos2 β + cos2 γ =1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.9) |
|
||||||||||||||||||||||||||||||
где α, β,γ |
- углы между вектором |
|
|
и осями X ,Y, Z в ДСК соответственно. |
||||||||||||||||||||||||||||||||||||||||||||||||||
a |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Если в ДСК точка A = (x, y, z) , то вектор |
|
= |
|
|
= (x, y, z) называется |
|||||||||||||||||||||||||||||||||||||||||||||||
rA |
OA |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
радиусом –вектором точки А. |
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rB |
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
X |
|
|
Рис. 1.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = (x1, y1, z1) и |
|||||||||||||||||||||||
|
|
Если вектор |
a |
AB |
в ДСК определен началом |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
концом B = (x2 , y2 , z2 ) , то координатами вектора |
|
являются числа |
|||||||||||||||||||||||||||||||||||||||||||||||||||
AB |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x = x2 − x1, |
y = y2 − y1, z = z2 − z1 , (рис. 1.9) |
т.е. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
= (x2 − x1) |
|
+ ( y2 − y1) |
|
+ (z2 − z1) |
|
= (x2 − x1, y2 − y1, z2 − z1) = |
||||||||||||||||||||||||||||||||||||||||||||||
|
AB |
i |
j |
k |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rB |
rA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.10) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
AB = |
(x |
2 |
− x )2 |
+ ( y |
2 |
− y )2 |
+ (z |
2 |
− z )2 . |
|
|
|
|
|
(1.11) |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Если векторы a = (x1, y1, z1) и b = (x2 , y2 , z2 ) коллинеарны, то их ко-
ординаты пропорциональны, т.е. условием коллинеарности двух векторов является равенство
7

x1 |
= |
y1 |
= |
z1 |
. |
(1.12) |
x2 |
y2 |
|
||||
|
|
z2 |
|
|||
1.1. По заданным векторам a и b построить вектор 3a − 2b. ∆ Решение задачи приведено на рис. 1.10
|
-b |
b |
|
3a – 2b |
|
-b |
|
|
|
a |
|
a |
a |
a |
|
|
|
|
|
Рис. 1.10 |
|
|
|
▲ |
|||||
|
|
1.2. Найти координаты и длину вектора |
d |
= 2 |
a |
− |
b |
+3 |
c |
, если |
||||
|
a |
= (2,3,1), |
b |
= (−2,3,4), |
c |
= (−1,0,5) . |
|
|
|
|
|
|
|
|
∆ Согласно линейным операциям над векторами, имеем
|
d |
= 2 |
a |
− |
b |
+3 |
c |
= 2(2,3,1) − (−2,3,4) +3(−1,0,5) = |
|
|
= (4,6,2) + (2,−3,−4) + (−3,0,15) = (4 + 2 −3, 6 −3 + 0, |
2 − 4 +15) = (3,3,13) |
|||||||
По формуле (1.6) d = 9 +9 +169 = 187 . |
▲ |
||||||||
1.3. Найти единичный вектор, направленный по биссектрисе угла между векторами a = (3,−2,1) и b = (1,2,3) .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 и |
|
0 векторов |
|
и |
|
|
|
||||||||||||||
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
Найдем орты |
a |
b |
a |
b |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 = |
|
|
1 |
|
|
|
· a = |
1 (3,−2,1) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 1.11): |
a |
|
|
|
|
|
|
; |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
ao |
|
|
|
|
ao + bo |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
14 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
co |
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
0 |
|
|
b = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
bo |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= b |
|
14 (1,2,3). |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
Рис. 1.11 |
|
0 + |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Тогда вектор |
|
|
= |
|
|
|
|
|
и будет направлен по биссектрисе искомого угла |
|||||||||||||||||||||||||||||||||||||||||||||
OA |
a |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 вектора |
|
равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
(диагональ ромба). Орт |
|
|
c |
AB |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
c |
|
= |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
+b |
. Но a |
|
+b |
|
= |
|
|
|
|
|
|
|
|
|
|
|
(4,0,4) |
, |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
a |
+ b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
a0 + b0 = |
|
|
|
|
|
16 + 0 +16 = |
|
|
= |
|
. Тогда |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
8

c0 = |
7 |
1 |
|
(4,0,4) = 1 |
|
|
|
(1,0,1). |
|
|
|
▲ |
||||||||
|
4 |
14 |
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
, чтобы выполня- |
||
1.4. Как должны быть связаны ненулевые векторы |
a |
b |
||||||||||||||||||
лось соотношение |
|
a |
+ |
b |
|
= |
|
a |
|
− |
|
b |
|
? |
|
|
|
|
||
a
b
∆ Векторы a и b должны быть коллинеарными и противоположно направленными
(a ↑↓ b) и, кроме того, a > b (рис. 1.12) . ▲
Рис. 1.12
1.5. В пространстве зафиксированы четыре точки А, В, С и Д. Точки P и Q – середины отрезков [АС] и [ВД] соответственно. Доказать, что
PQ = 12 (AB +CD).
B K C
P Q
Q
∆ Пусть К – середина отрезка [ВС] (рис. 1.13). Тогда РК – средняя линия ∆ABC , и, значит,
PK = (1/ 2)AB . Аналогично, KQ = (1/ 2)CD .
Следовательно,
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
+ |
|
= |
1 |
( |
|
+ |
|
|
|
|
). |
|
|||||||||
|
|
|
|
|
|
|
|
PQ |
PK |
KQ |
AB |
CD |
▲ |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
A |
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||
Рис. 1.13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1.6. Показать, что векторы |
|
|
|
|
|
= (1,0,1), |
|
= (1,−2,0), |
|
= (0,3,1) |
обра- |
|||||||||||||||||||||||||
a |
b |
c |
||||||||||||||||||||||||||||||||||
зуют базис пространства R3 |
|
и найти координаты вектора |
|
= (2,7,5) |
в этом |
|||||||||||||||||||||||||||||||
|
d |
|||||||||||||||||||||||||||||||||||
базисе. |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
Для векторов |
a |
|
|
|
b |
|
|
c |
|
составим равенство (1.2): |
|
||||||||||||||||||||||||
|
α1 |
|
+α2 |
|
+α3 |
|
= |
|
. |
(1.12) |
||||||||||||||||||||||||||
|
a |
b |
c |
0 |
||||||||||||||||||||||||||||||||
Покажем, что оно имеет место лишь в случае, когда α1 =α2 =α3 = 0. Действительно, векторное равенство (1.12) равносильно системе
α1 +α2 |
= 0, |
|
α1 = 0, |
||
− 2α2 + 3α3 = 0, |
|
|
|
= 0, |
|
|
α2 |
||||
α1 |
+α3 = 0 |
|
|
|
= 0. |
|
|
α3 |
|||
9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, векторы a, |
b, |
c линейно независимы и, следовательно, |
образуют |
||||||||||||||||||||||||||||||||
базис. Координаты вектора |
|
|
в этом базисе |
обозначим α, β, |
γ , т.е. |
||||||||||||||||||||||||||||||||
d |
|||||||||||||||||||||||||||||||||||||
|
|
=α |
|
+ β |
|
|
+γ |
|
|
, что, |
|
согласно условию, равносильно системе |
|
|
|
||||||||||||||||||||||
d |
a |
b |
c |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
2 =α + β, |
|
|
|
|
|
|
α = 4, |
|
|
|
|
|
|
||||||||||||||||||||||
7 = |
|
|
|
− 2β2 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
3γ, |
β = −2, |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
5 =α |
|
|
|
|
|
|
|
|
|
|
|
|
+γ |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ =1. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
= 4 |
|
− 2 |
|
+ |
|
, т.е. в базисе { |
|
|
|
, |
|
|
} координатами вектора |
|
|
||||||||||||||||||
|
|
Итак, |
d |
a |
b |
c |
a, |
|
b |
|
c |
d |
|||||||||||||||||||||||||
являются числа 4, -2, 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
▲ |
|
|
|
||||||||||||||||
1.7. В треугольнике АВС проведены медианы АД, ВЕ, CF. Показать, что
AD + BE +CF = 0.
1.8. Как должны быть связаны ненулевые векторы a и b , чтобы имели место соотношения:
|
|
|
+ |
|
|
|
|
= |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
− |
|
|
= |
|
|
|
+ |
|
|
|
|
|
3) |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1) |
a |
b |
|
|
a |
|
b |
|
;2) |
|
a |
b |
|
|
a |
|
b |
|
; |
a |
a |
b |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
+ |
|
=α |
|
|
|
− |
|
|
|
|
|
|
|
|
+ |
|
|
|
> |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
= |
|
1 |
|
|
|
|
; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4) |
a |
b |
|
|
a |
b |
; |
|
|
5) |
|
|
a |
b |
|
|
|
|
a |
b |
|
|
; |
|
|
|
|
|
6) |
|
|
|
|
a |
b |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
+ |
|
делит угол между векторами |
|
и |
|
пополам. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7) |
вектор |
a |
a |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
b |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
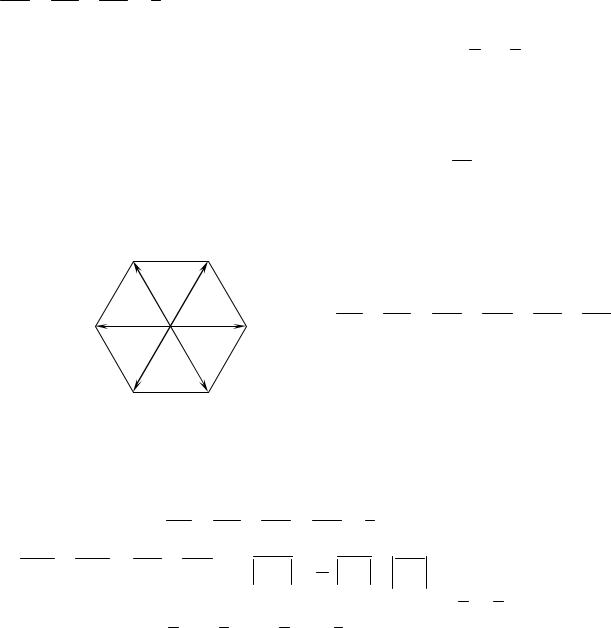
1.9. |
B |
C |
Пусть О – центр правильного шестиугольника АВСДЕF (рис. 1.14). Найти сумму векторов
A  O D
O D
OA +OB +OC +OD +OE +OF .
F E
Рис. 1.14
1.10 . Пусть А, В, С, Д – некоторые точки пространства или плоскости, М – середина отрезка [AB], N – середина отрезка СД, О – середина отрезка [M
N]. Доказать, что 1) OA +OB +OC +OD = 0;
2)MN + MN = BC + AD ; 3) MN ≤ 12 (BC + AD ).
1.11.Доказать, что для неколлинеарных векторов a и b равенство
m1 a + n1b = m2 a + n2 b
10

равносильно системе равенств |
|
|
||
m1 = m2 , |
|
n1 = n2 . |
||
|
|
|
|
неколлинеарны. При каком α векторы |
1.12. Векторы |
a |
и |
b |
|
c = (α −1)a + b и d = (2 + 3α)a − 2b коллинеарны?
1.13 . Дан треугольник АВС. На прямых (АВ), (ВС), (СА), проходящих через А и В, В и С, С и А, выбраны соответственно точки M, N, P так, что
|
|
=α |
|
, |
|
|
= β |
|
, |
|
|
= γ |
|
|
, |
α, β,γ R . |
При каком условии |
||||
|
AM |
AB |
BN |
BC |
|
CP |
CA |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
векторы |
|
|
CM , |
|
AN |
|
и |
|
|
BP |
образуют |
треугольник, т.е. |
|||||||||
CM + AN + BP = 0?
1.14 . На сторонах ВС и СД параллелограмма АВСД взяты точки F и Е так, что BF : FC = µ ,
B |
F |
C |
|
DE |
|
: |
|
EC |
|
= λ, где |
λ и µ - заданные |
|
|
|
|
||||||||
|
|
|
|
|
|
|
O
E
положительные числа (рис. 1.15). Прямые (FD) и (АЕ) пересекаются в точке О. Найти
A
D
Рис. 1.15
отношение FO : OD .
1.15. Показать, что векторы |
|
, |
|
|
|
|
|
|
|
|
, |
|
образуют базис пространства R3 и |
|||||||||||||||||||||||
a |
|
|
|
|
b |
c |
||||||||||||||||||||||||||||||
найти координаты вектора |
d |
в этом базисе: |
d = (5,7,8); |
|||||||||||||||||||||||||||||||||
1) |
|
|
|
a |
= (4,5,2), |
|
b |
= (3,0,1), |
c |
|
|
= (−1,4,2), |
||||||||||||||||||||||||
2) |
|
|
|
|
= (3,−5,2), |
|
|
|
|
|
|
|
= (4,5,1), |
|
|
|
|
|
|
= (−3,0,4), |
d = (−4,5,−16) ; |
|||||||||||||||
|
a |
|
|
|
b |
|
|
|
|
c |
||||||||||||||||||||||||||
3) |
|
|
|
|
= (−2,3,5), |
|
|
|
|
|
= (1,−3,4), |
|
|
|
|
= (7,8,−1), |
d = (1,20,1); |
|||||||||||||||||||
|
|
a |
|
|
|
b |
|
|
c |
|||||||||||||||||||||||||||
4) |
|
|
|
= (1,3,5), |
|
= (0,2,0), |
|
|
= (5,7,9), |
d = (0,4,16). |
||||||||||||||||||||||||||
|
a |
b |
c |
|||||||||||||||||||||||||||||||||
1.16. Вычислить длину и направляющие косинусы вектора |
|
, если: |
||||||||||||||||||||||||||||||||||
BA |
||||||||||||||||||||||||||||||||||||
1) |
A = (1,−2,3), |
|
|
B = (0,−1,2); |
2) |
A = (0,−3,6), |
B = (−12,−3,−3); |
|||||||||||||||||||||||||||||
3) |
A = (3,3,−1), |
|
|
B = (5,5,−2); |
4) |
A = (−1,2−,3), |
B = (3,4,−6) . |
|||||||||||||||||||||||||||||
1.17. Для векторов a = (1,5,3), b = (6,−4,−2), c = (0,−5,7),
11

d = (−20,27,−35) подобрать числа α, β, γ |
так, чтобы векторы |
|
, |
||||||
d |
|||||||||
α |
|
, β |
|
, γ |
|
образовывали замкнутую линию, |
если начало последующего |
||
a |
b |
c |
|||||||
вектора совместить с концом предыдущего. |
|
|
|
||||||
1.18. Даны радиусы – векторы вершин ∆ABC : rA = (3,2,1), rB = (1,4,1) rC = (1,2,3) . Показать, что треугольник равносторонний.
1.19. |
Доказать, что точки A = (1,0,−2), |
|
B = (−3,4,2), C = (0,1,3), |
|||||||||||||
D = (2,−1,1) лежат в одной плоскости. |
|
|
|
|
|
|||||||||||
|
В ДСК вектор |
|
|
|
= |
|
образует один и тот же угол с осями коор- |
|||||||||
1.20. |
OA |
rA |
||||||||||||||
динат. Чему он равен? |
|
|
|
|
|
|||||||||||
|
Вектор |
|
образует углы α = 45o , |
β = 60o , γ =120o с осями |
||||||||||||
1.21. |
a |
|||||||||||||||
|
|
|
|
= 2. Найти координаты вектора |
|
. |
||||||||||
X, Y, Z соответственно, |
|
a |
|
a |
||||||||||||
|
В точке A = (−3,−2) приложена сила |
|
, проекция которой Fy на |
|||||||||||||
1.22. |
F |
|||||||||||||||
ось Y равна –1, а проекция Fx на ось X положительна. Найти конец вектора
|
AB |
, изображающего эту силу, если |
F = 5 2 . |
|
|
|
|
|
|
||||||||
|
|
1.23. Даны точки |
A = (1,2), |
B = (3,5), |
C = (5,2) и |
D = (2,−2) . В |
|||||||||||
|
|
|
1 = |
|
|
|
2 = |
|
, |
|
|
3 = |
|
. |
|
||
точке А приложены силы |
|
|
AB |
, |
|
AC |
AD |
Найти проекции |
|||||||||
|
F |
F |
F |
||||||||||||||
на оси координат равнодействующей F этих сил и ее величину.
1.2. Деление отрезка в данном отношении. Скалярное произведение векторов. Ортогональная составляющая вектора вдоль другого вектора.
|
|
|
Пусть А и В – различные точки, заданные |
||||||||||
|
M |
l |
|
|
|
|
|
|
|
|
|
|
|
B |
радиусами-векторами rA и rB относи- |
||||||||||||
|
|
||||||||||||
A |
|
|
тельно полюса O , λ - положительное |
||||||||||
|
|
число. Говорят, что точка М делит отре- |
|||||||||||
rB |
r |
|
зок [AB] в отношении λ, если |
||||||||||
rA |
|
||||||||||||
|
|
|
AM |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
O |
|
|
|
|
|||||||||
|
|
|
|
|
MB |
|
= λ. При этом λ > 0 , если М |
||||||
|
|
|
|
|
|
||||||||
Рис. 1.16 |
|
|
внутри отрезка [AB], и λ < 0 , если М |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
12

вне его. В первом случае говорят, что точка М |
делит отрезок [AB] внутренним |
|||||||||||||||||||||||||||||||||||||||||||||||||
образом, во втором – внешним образом. |
A = (xA , yA , zA ) и |
B = (xB , yB , zB ), |
||||||||||||||||||||||||||||||||||||||||||||||||
Если известны координаты точек |
||||||||||||||||||||||||||||||||||||||||||||||||||
то координаты точки M = (xM , yM , zM ) вычисляются по формулам: |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x |
A |
+ λx |
B |
|
|
|
|
|
|
|
|
|
|
|
|
y + λy B |
|
|
|
|
|
|
z + λz B |
|
|
||||||||||||||||||||||
x |
M |
= |
|
|
|
|
|
|
|
|
, y |
M |
= |
|
|
|
|
|
|
A |
|
|
|
, |
z |
M |
= |
|
|
|
A |
|
|
. |
(1.13) |
|||||||||||||||
|
1+ λ |
|
|
|
|
|
|
|
|
1 + λ |
|
|
|
1 + λ |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Если М – середина отрезка [AB], то ее координаты (λ =1) |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x |
A |
+ x |
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y + y B |
|
|
|
|
|
|
|
|
z + z B |
|
|
||||||||||||||||||
x |
M |
= |
|
|
|
|
, |
|
|
|
y |
M |
= |
|
|
|
|
|
A |
|
|
, |
z |
M |
= |
|
|
|
A |
|
|
. |
(1.14) |
|||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 + λ |
|
|
|
1+ λ |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Равенства (1.13) равносильны векторному равенству |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= ( |
|
|
|
+ λ |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rA |
rB |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
(1.15) |
||||||||||||||||||||
|
|
|
|
|
r |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1+ λ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Скалярным произведением ненулевых векторов |
a |
и |
b |
называется число, |
||||||||||||||||||||||||||||||||||||||||||||||
обозначаемое ( |
a |
, |
b |
) и равное |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
, |
|
|
|
) = |
|
|
|
|
|
|
|
|
|
|
cosϕ, |
|
|
|
|
|
|
|
|
|
|
|
(1.16) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
a |
b |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
где ϕ = (a,^ b) .
Если один из векторов нулевой, то скалярное произведение по определе-
нию равно нулю: ( |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
a |
0) = (0,b) = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Скалярное произведение ( |
|
|
|
, |
|
|
|
|
|
) , равное |
|
|
|
|
2 , |
|
||||||||||||||||||||||||||||||||||
a |
|
a |
|
a |
|
называется скалярным квад- |
||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
ратом вектора |
a |
|
и обозначается |
a |
, |
т.е. |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
, |
|
|
) = |
|
|
|
2 = |
|
|
|
|
|
|
|
|
2 . |
(1.17). |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
a |
a |
|
a |
|
|||||||||||||||||||||||||||||||||
Из этого равенства следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = |
(a, a) . |
(1.18) |
||||||||||||||||||||||||||||
Другим определением скалярного произведения является равенство |
||||||||||||||||||||||||||||||||||||||||||||||||||
( |
|
, |
|
|
) = |
|
|
|
пр |
|
|
|
|
= |
|
|
пр |
|
|
|
. |
|
||||||||||||||||||||||||||||
a |
b |
a |
b |
b |
a |
(1.19) |
||||||||||||||||||||||||||||||||||||||||||||
|
а |
b |
||||||||||||||||||||||||||||||||||||||||||||||||
Скалярное произведение обладает свойствами: 1o.(a,b) = (b, a) (коммутативность).
2o.(λ |
|
|
, |
|
) = ( |
|
λ |
|
|
) = λ( |
|
|
|
, |
|
|
) |
(ассоциативность), где λ R . |
|||||||||
a |
b |
a, |
b |
a |
b |
||||||||||||||||||||||
3o.( |
|
, |
|
+ |
|
) = ( |
|
, |
|
) + ( |
|
, |
|
) |
(дистрибутивность). |
||||||||||||
a |
b |
c |
a |
b |
a |
c |
|||||||||||||||||||||
13

4o . Ненулевые векторы a и b перпендикулярны (ортогональны) тогда и только тогда , когда их скалярное произведение равно нулю, т.е.
|
|
|
|
|
|
( |
|
|
|
, |
|
|
|
|
|
) = 0 |
|
|
|
|
|
|
|
|
|
(1.20) |
||||||||||||||||
|
a |
b |
a |
b |
||||||||||||||||||||||||||||||||||||||
- условие ортогональности двух векторов. |
|
|||||||||||||||||||||||||||||||||||||||||
5o. |
|
↑↑ |
|
( |
|
|
, |
|
) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
a |
b |
a |
b |
a |
b |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
↑↓ |
|
( |
|
, |
|
) = − |
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
a |
b |
a |
b |
a |
b |
|
||||||||||||||||||||||||||||||||||
6o. (a,b) > 0 0 ≤ϕ < π |
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(a,b) < 0 π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
2 |
|
< ϕ ≤ π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7o. − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤ ( |
|
|
, |
|
|
) ≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
a |
|
|
b |
|
a |
b |
|
a |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
и проекция вектора |
|
|
на вектор |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Косинус угла между векторами |
a |
a |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
выражаются соответственно формулами : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
, |
|
|
|
|
|
) |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosϕ = |
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.21) |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
( |
|
, |
|
|
) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пр |
|
|
|
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.22) |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (ax , ay , az ), |
|
= (bx ,by ,bz ), |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
Если в ДСК |
|
|
|
|
|
a |
b |
то |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
( |
|
|
, |
|
|
|
) = (axbx + ayby + azbz ), |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
|
|
(1.23) |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
cosϕ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
axbx + ayby + azbz |
|
2 , |
(1.24) |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ax |
2 + ay |
2 + az |
2 |
|
|
|
|
bx |
2 +by |
2 +bz |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
пр |
|
|
b = |
axbx |
+ ayby + azbz |
. |
|
|
|
(1.25) |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
|
|
|
ax |
2 + ay 2 + az 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
В координатной записи условие ортогональности векторов |
a |
и |
b |
имеет |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вид |
|
|
|
|
axbx + ayby + azbz = 0. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
|
(1.26) |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a
d
b
ab
Ортогональной составляющей вектора a вдоль вектора b называется вектор ab , коллинеарный b , такой что
d = a − ab b (рис. 1.17). Для вектора
ab справедлива формула
Рис. 1.17
14

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b = |
( |
|
|
, |
|
) |
|
|
|
|
|
|
|
|
|
= |
|
|
(a,b) |
|
|
= |
|
пр |
|
|
|
|
|
. |
|
|
|
|||||||
|
|
|
|
a |
b |
(1.27) |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
a |
b |
a |
a |
|||||||||||||||||||||||||||||||||||||||
|
|
|
b |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|||||||||||||||||||||||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- вектор перемещения точки под действием силы |
|
, то работа |
||||||||||||||||||||||||||||||||||||||||
Если |
s |
F |
||||||||||||||||||||||||||||||||||||||||||
этой силы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = ( |
|
, |
|
) . |
(1.28) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
s |
|||||||||||||||||||||||||
1.24. Найти точку пересечения биссектрисы угла А |
с противолежащей |
|||||||||||||||||||||||||||||||||||||||||||
стороной ВС треугольника АВС, если A = (4,1), B = (7,5), C = (−4,7). ∆ Из свойства биссектрисы внутреннего угла ∆ АВС известно, что
A
C D B
Рис. 1.18
|
AC |
|
= |
|
|
CD |
|
|
= λ, |
т.е. точка D де- |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||
|
AB |
|
|
|
|
DB |
|
|
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
лит сторону СВ в отношение λ = AC / AB . Находим
AC =10, AB = 5 т.е. λ = 2. По
формулам (1.13) получаем |
|
|
|
|
|
|
|
|
|
|
|
||
xD = |
xc + 2xB |
|
= |
− |
4 + 2 |
7 |
= |
10 |
; |
||||
1+ 2 |
|
|
|
3 |
|
|
3 |
||||||
|
|
|
|
|
|
|
|
|
|||||
yD = |
yc + 2yB |
= |
|
7 + 2 5 |
= |
17 |
. |
|
|||||
1+ 2 |
|
|
|
3 |
|
3 |
|
||||||
|
|
|
|
|
|
|
|
||||||
Итак, D = (10 / 3, 17 / 3). |
|
|
|
|
|
|
|
|
|
|
▲ |
||
1.25. Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую из медиан в отношении 2:1, считая от вершины.
∆ B
a
M K
a Q
A |
N |
b |
C |
|
|||
|
|
|
P
Рис. 1.19
Пусть в ∆ АВС точки К и М – середины сторон ВС и АВ соответственно, Q – точка пересечения медиан АК и СМ (рис. 1.19). Обозначим λ = CQ / QM ,
µ = AQ / QK и покажем, что λ = µ = 2. Положим AM = a (тогда AB = 2a), AC = b. По
15

формуле |
(1.15) |
|
|
|
деления |
|
|
отрезка |
|
[CM ] |
точкой |
Q в отношении λ |
|
|
имеем |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
= ( |
|
|
|
|
+ λ |
|
|
|
)/(1 + λ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
+ |
|
= |
|
+ |
|
AQ |
|
= |
||||||||||||||||||||||||
|
AQ |
b |
a |
|
|
Следовательно, |
AK |
AQ |
QK |
AQ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
µ |
|
|
||
|
µ +1 |
|
|
|
|
+ λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
= |
b |
a |
. Точка |
|
|
К делит отрезок [СВ] |
в отношении 1:1, |
поэтому |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
µ |
|
|
|
|
|
|
|
1+ λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
= ( |
|
+ |
|
|
|
)/ 2 = ( |
|
|
|
+ 2 |
|
|
|
|
)/ 2 . Из последних двух равенств получаем |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
AK |
AC |
AB |
b |
a |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
µ +1 |
|
|
|
+ λ |
|
|
|
= |
|
|
|
+ 2 |
|
|
. |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
a |
b |
a |
|
|
|
(1.29) |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
µ |
|
|
|
|
|
|
|
1+ λ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Так как векторы |
a |
и |
b |
|
неколлинеарны, то из (1.29) вытекает, что |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
µ +1 |
|
|
|
|
|
1 |
|
|
|
|
= |
|
1 |
, |
|
|
|
|
|
|
|
|
µ +1 |
|
|
1 |
|
|
|
|
= 1 |
λ = 2. |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
+ |
|
λ |
2 |
|
|
|
|
|
|
|
|
|
|
+ λ |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
µ |
|
|
|
|
|
|
|
|
|
|
µ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Следовательно, |
µ +1 |
= |
3 |
|
µ = 2 . Итак, доказано, что точка Q, |
принад- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
µ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
лежащая медиане СМ, делит ее в отношении 2:1. Она лежит и на медиане АК и делит ее в том же отношении. Аналогичным образом устанавливается, что точка Q лежит и на медиане BN и делит ее в отношении 2:1, считая от вершины В. Следовательно, все три медианы ∆ АВС пересекаются в одной точке и делятся
этой точкой в отношении 2:1, считая от вершины. |
|
▲ |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
справедливы следующие |
||||||||||
1.26. Доказать, что для любых векторов |
a |
b |
||||||||||||||||||||||||||||||
равенства: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
( |
|
± |
|
)2 = |
|
2 + |
|
|
2 ± 2( |
|
, |
|
) . |
|
|
|
|
(1.30) |
||||||||||||||
a |
b |
a |
b |
a |
b |
|||||||||||||||||||||||||||
∆ Ограничимся случаем неколлинеарных векторов |
a |
и |
b |
|
(в случае кол- |
|||||||||||||||||||||||||||
линеарности равенства (1.30) также справедливы). |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
от одной точки : |
|
= |
|
, |
|
|
= |
|
. Рассмотрим |
|||||||||||||||||||
Отложим векторы |
a |
и |
b |
OA |
a |
OB |
b |
|||||||||||||||||||||||||
параллелограмм ОВСА (рис. 1.20 – 1.22). |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
B |
a - b |
a + b |
C |
B |
a + b |
C |
B |
|
|
C |
|
|
b |
|
a - b |
|
|
a - b a + b |
|
|
||||
|
|
|
|
b |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
M |
a |
A |
N |
|
|
|
M |
O |
a |
N |
A |
O = M |
a |
A = N |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
Рис. 1.20 |
Рис. 1.21 |
Рис. 1.22 |
16

Обозначим a = a , b = b , ϕ = (a,^ b) , M и N – основания перпенди-
куляров, опущенных на прямую (ОА) из точек В и С соответственно. По теореме Пифагора для треугольников АМВ и ONC имеем:
|
|
AB |
|
2 = |
|
AM |
|
2 + |
|
MB |
|
2 , |
|
OC |
|
2 = |
|
ON |
|
2 + |
|
NC |
|
2 . |
(1.31) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
В случае острого угла ϕ (рис. 1.20) |
|
AM |
|
= |
|
OA |
|
− |
|
OM |
|
= a −b cosϕ, |
||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
MB = NC = bsin ϕ, ON = OA + AN = a + b cosϕ . Если ϕ = 90o (рис. 1.21), то AM = OA = a = a −b cosϕ, MB = NC = b = bsin ϕ,
ON = OA = a = a + b cosϕ . Если ϕ - тупой (рис. 1.22), то
AM = OA + OM = a +b cos(180o −ϕ) = a −b cosϕ,
MB = NC = bsin(180o −ϕ) = bsinϕ, ON = OA − AN = a + b cosϕ . Та-
ким образом, во всех случаях |
|
|
AM |
|
= a −b cosϕ, |
|
MB |
|
= |
|
NC |
|
= bsin ϕ, |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ON |
|
|
|
= a + b cosϕ . Тогда по формулам (1.31) имеем |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
( |
|
|
− |
|
|
)2 = |
|
|
|
AB |
|
2 = (a −b cosϕ)2 + (bsinϕ)2 = |
||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= a2 + b2 − 2ab cosϕ = |
|
|
2 + |
|
|
2 − 2( |
|
|
, |
|
|
), |
||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
a |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
( |
|
|
+ |
|
)2 = |
|
OC |
|
2 = (a +bcosϕ)2 +(bsinϕ)2 = |
|||||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + |
|
|
2 + 2( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
▲ |
|||||||||||
= a2 +b2 + 2abcosϕ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
a |
b |
a |
, |
b |
). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
1.27. |
|
|
|
|
|
|
|
|
|
Пусть |
|
a |
|
|
|
|
|
b |
|
|
|
|
- единичные векторы. Вычислить |
|||||||||||||||||||||||||||||||||||
(3 |
|
− 4 |
|
, |
|
2 |
|
+ 5 |
|
), если |
|
a +b = |
3 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
a |
b |
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
∆3 = a +b 2 = a2 +b2 + 2(a,b) =1+1+ 2(ab) (a,b) =1/ 2 . Тогда
(3a − 2b, 2a +5b) = 6a2 − 20b2 + 7(a,b) = 6 − 20 + 7 / 2 = −21/ 2. ▲
1.28. Найти угол ϕ между векторами a = i + j − 4k и
b = i − 2 j + 2k и проекцию вектора a + b на вектор c = 3i − 4 j +12k .
∆ Используя координатную форму скалярного произведения (1.23) и
формулы (1.21), (1.22), получаем |
|
|
|
|||
cosϕ = |
(a,b) |
= |
1 1+1 (−2) + (−4) 2 |
= − |
1 |
ϕ = 3π / 4, |
|
a b |
|
12 +12 + (−4)2 12 + (−2)2 + 22 |
|
2 |
|
17

|
|
|
|
|
+ |
|
) = |
( |
|
+ |
|
|
|
, |
|
) |
= |
( |
|
, |
|
) + ( |
|
, |
|
) |
= − 49 + 35 = − |
14 |
. |
|
||||||||
пр |
|
|
( |
|
a |
b |
c |
a |
c |
b |
c |
|
||||||||||||||||||||||||||
|
|
a |
b |
▲ |
||||||||||||||||||||||||||||||||||
c |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
c |
|
13 |
13 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1.29. Три силы F1 = (3,4,2), F 2 = (2,3,−5), F 3 = (−3,−2,4) при-
ложены к одной точке. Найти работу равнодействующей этих сил, когда ее точ-
ка приложения, двигаясь |
прямолинейно, |
перемещается |
|
из положения |
|||||||||||||||||||
M1 = (5,3,−7) в положение |
M 2 = (4,−1,−4) . |
|
|
|
|
1 + |
|
2 + |
|
3 = |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
этих сил: |
|
= |
|
|
|
|||||||
∆ Находим равнодействующую |
F |
F |
F |
F |
F |
||||||||||||||||||
= (2,5,1) . Вектор перемещения |
|
= |
|
|
= (−1,−4,3). По формуле (1.28) |
||||||||||||||||||
s |
M1M |
2 |
|||||||||||||||||||||
искомая работа |
A |
= ( |
F |
|
s |
) = 2 (−1) + 5 |
(−4) |
+1 3 = −19 . |
|
|
|
▲ |
|||||||||||
1.30. Длина ребра основания АВС правильной треугольной призмы ABCA1B1C1 равна а. Точки M, N, P, Q – середины ребер AB, AC, A1C1 ,
C1B1 . Длина проекции вектора MP на прямую (NQ) = a / 4. Найти длину высоты призмы.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пр(NQ) MP |
|
2 = |
( |
|
|
|
, |
|
|
|
|
|
) 2 |
= |
a2 |
|
|||||||||
|
|
|
|
|
|
∆ По условию, |
MP |
NQ |
(формула 1.27). Пусть |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
= |
|
|
|
|
|
|
, |
|
= |
|
|
|
|
, |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
NQ |
|
16 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Тогда : |
|
|
|
|||||||||||||||||||||||||||
a |
BA |
b |
BC |
|
c |
BB1 |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
= |
|
|
|
|
= a, ( |
|
, |
|
) = a2 / 2, ( |
|
|
|
) = ( |
|
|
|
) = 0 |
(призма правильная). Иско- |
|||||||||||||||||||||||||
|
a |
|
|
b |
|
a |
b |
a |
|
,c |
b, |
|
c |
||||||||||||||||||||||||||||||||||
мая длина h = c . Так как MP = (1/ 2)b + c, NQ = (−1/ 2)a + c, то
(MP, NQ) = −(1/ 4)(a,b) + c2 = h2 − a2 / 8,
NQ 2 = (1/ 4)(a)2 + c2 = h2 + a2 / 4 . Следовательно, для величины x = h2
получаем уравнение
(MP, NQ)2 = (x − a2 / 8)2 = (a2 /16)(x + a2 / 4) = (a2 /16) NQ 2 или
x2 − (5 /16)a2 x = 0 . Так как x ≠ 0 , то h2 = (5 /16)a2 , т.е. h = a 5 / 4. ▲
5 / 4. ▲
1.31. Вычислить длину медиан треугольника, зная координаты его вер-
шин: A = (3,−2), B = (5,2), C = (−1,4).
1.32. Отрезок АВ перемещается так, что концы его все время остаются на двух неподвижных прямых: конец А скользит по прямой, параллельной оси Х и проходящей над ней на расстоянии трех единиц; конец В скользит по прямой, параллельной оси Y и проходящей слева от нее на расстоянии двух единиц.
18
Определить положение концов отрезка в тот момент, когда середина отрезка совпадает с точкой М = (3, 1).
1.33.Прямая линия отсекает на оси Х отрезок ОА = 4 и на оси Y – отрезок ОВ = 7. Найти координаты основания перпендикуляра, опущенного из начала координат на данную прямую.
1.34.Найти координаты центра тяжести ∆ АВС, если A = (x1 , y1 , z1 ),
B = (x2 , y2 , z2 ) , C = (x3, y3, z3 ) .
1.35.Найти центр тяжести четырехугольника однородной доски, зная, что
углы доски расположены в точках A = (4,4), B = (5,7), C = (10,10),
D= (12,4).
1.36.Вычислить координаты центра тяжести фигуры, размеры и форма
C |
24 |
D |
|
|
|
||
|
|
|
2 |
14 |
|
|
E |
|
F |
||
|
|
|
|
A |
10 |
B |
|
|
|
||
которой даны на рис. 1.23, приняв за оси координат прямые (АВ) и (АС).
Рис. 1.23
1.37. Доказать, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=11, |
|
|
|
= 23, |
|
|
|
|
|
− |
|
|
|
|
= 30. Найти |
|
|
+ |
|
|
|
и угол |
|||||||||||
1.38. |
|
|
|
Дано: |
|
a |
|
b |
|
|
a |
b |
|
a |
b |
|||||||||||||||||||||||||||||||||||||
ϕ = ( |
|
|
,^ |
|
|
|
) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
ортогональны тогда и только тогда, ко- |
||||||||||||||||||||||||||||||||
1.39. |
|
|
Доказать, что векторы |
a |
b |
|||||||||||||||||||||||||||||||||||||||||||||||
гда |
|
|
|
+ |
|
|
= |
|
|
− |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
a |
b |
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
( |
|
, |
|
) |
|
|
ортогонален вектору |
|
. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
− |
a |
b |
|||||||||||||||||||||||||||||||||||||
1.40. |
|
|
Доказать, что вектор |
d |
b |
|
a |
a |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.41. Доказать, что скалярное произведение не изменится, если к одному из них прибавить вектор, ортогональный другому вектору – сомножителю.
19

1.42. |
|
|
В ∆ АВС |
|
|
AB |
|
= c, |
|
AC |
|
|
= b, |
|
|
BC |
|
= a . Найти длину медианы |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
СМ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
+ 2 |
|
= |
|
, |
|
|
|
|
=1, |
|||||||||||||
1.43. |
|
|
Векторы |
a |
b |
c |
|
|
|
удовлетворяют условиям: |
a |
b |
c |
0 |
|
a |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
= 4 , |
|
|
|
|
|
= 2. Вычислить величину |
µ = ( |
|
|
, |
|
) + ( |
|
, |
|
) + ( |
|
, |
|
) . |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
b |
|
|
|
|
c |
|
|
a |
b |
b |
c |
c |
a |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
1.44. |
|
|
Дано: |
|
|
|
|
= 3, |
|
|
|
|
|
|
= 2, |
( |
|
,^ |
|
) =120o. Найти длины векторов |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a |
|
b |
a |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
p = a + 2b и q = 2a −b, их скалярное произведение и угол ϕ между ними.
1.45. Длины ненулевых векторов a и b равны. Найти угол ϕ между
этими векторами, если известно, что векторы p = a + 3b и q = 5a + 3b ортогональны.
1.46.В ∆ АВС проведены медианы АД, ВЕ и CF. Вычислить величину
λ= (BC, AD)+ (CA, BE)+ (AB,CF ).
1.47.Доказать, что при любом расположении точек А, В, С, Д на плоско-
сти имеет место равенство µ = 0, где µ = (BC, AD)+ (CA, BD)+
+(AB,CD).
1.48.В прямоугольной трапеции АВСД диагонали взаимно перпендикулярны, а отношение длин оснований BC : AD = λ. Найти отношение длин
диагоналей.
1.49.Определить угол между диагоналями АС и ВД выпуклого четырехугольника АВСД, если AB 2 + CD 2 = BC 2 + AD 2 .
1.50.Даны прямоугольник АВСД и точка М. Показать, что
а) ( |
|
, |
|
|
|
|
|
|
|
)= ( |
|
|
|
|
|
|
|
|
|
|
, |
|
|
); |
|
|
|
б) |
|
MA |
|
2 + |
|
MC |
|
2 = |
|
MB |
|
2 + |
|
|
MD |
|
2 . |
|
|
|
|
||||||||||||||||
MA |
MC |
MB |
MD |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
, |
|
компланарны. Найти длину вектора |
|
= |
|
+ |
|
− |
|
, |
||||||||||||||||||||||||||||||||||||||
1.51. Векторы |
a |
b |
c |
p |
a |
b |
c |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
= 3, |
|
|
|
|
|
= 2 , |
|
|
|
|
|
= 5 и |
( |
|
, |
|
) = ( |
|
, |
|
) = π / 3. |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
если |
|
a |
|
|
|
b |
|
|
|
|
c |
|
|
a |
b |
b |
c |
||||||||||||||||||||||||||||||||||||||||||||||||
1.52. Найти величины углов A, |
B, C треугольника АВС с вер- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
шинами A = (−1,−2,4), B = (−4,−2,0), |
|
|
|
|
C = (3,−2,1) . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
20

1.53. Вектор c , перпендикулярный к векторам a = (3,2,2) и b = = (18,−22,−5) , образует с осью Y тупой угол. Найти координаты вектора c , зная, что c =14.
1.54.Найти проекцию вектора a = (4,−3,2) на ось, составляющую одинаковые углы с осями координат.
1.55.Найти ортогональную составляющую вектора a вдоль вектора b :
1) |
|
= (−1,2,1), |
|
= (1,1,1) ; |
2) |
|
= (−2,1,−2), |
|
= (3,0,3). |
a |
b |
a |
b |
1.56.Найти вектор х, коллинеарный вектору a = (2,1,−1), удовлетворяющий условию (x, a) = 3.
1.57.Вектор c перпендикулярен оси Z , и, кроме того, (c, a) = 9,
(c,b) = −4 , где a = (3,−1,5) , b = (1,2,−3). Найти вектор c по этим данным.
1.58. Скорость разложена по трем взаимно перпендикулярным направлениям, одно из которых задано вектором a = (2,2,1) . Найти составляющую скорости v в направлении вектора a .
1.59. Даны векторы a = (2,−1,3), b = (1,−3,2), c = (3,2,−4) . Найти вектор d , удовлетворяющий условиям (a, d) = −5, (b, d) = −11, (c, d) = 20 .
1.60.Найти вектор b , перпендикулярный оси Z, если b = 2 , (a,b) = 4,
где (a) = (1,2,−7) .
1.61.Найти единичный вектор e, перпендикулярный оси Y и вектору
a= (4,3,2) .
1.3.Определители 2-го и 3-го порядков. Системы двух линейных уравнений с двумя неизвестными. Системы трех линейных уравнений с тремя неизвестными. Правило Крамера. Векторное произведение векторов.
Матрицей (квадратной) 2-го порядка называется таблица,
21

a |
a |
|
, |
A = 11 |
12 |
|
|
a21 |
a22 |
|
|
а таблица вида
|
a |
a |
||
|
11 |
12 |
||
A = |
a21 |
a22 |
||
|
a |
31 |
a |
32 |
|
|
|
||
матрицей 3-го порядка. Определителем 2-го порядка
число
a13 a23 - a33
матрицы или детерминантом А называется
|
A |
|
|
= det A = |
|
a11 |
|
|
a12 |
|
= a |
a |
22 |
− a |
|
|
a |
21 |
. |
|
|
|
(1.32) |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a21 |
a22 |
|
|
|
|
11 |
|
12 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Определителем 3-го порядка или детерминантом матрицы А называется |
||||||||||||||||||||||||||||||||||||
число |
|
a |
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
11 |
|
|
12 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
A |
|
= det a21 |
a22 |
|
a23 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
a |
31 |
|
|
a |
32 |
|
a |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= a |
|
a22 |
|
a23 |
|
− a |
|
a21 |
a23 |
|
+ a |
|
a21 |
|
a22 |
|
. |
(1.33) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
11 |
|
a32 |
|
a33 |
|
|
|
12 |
a31 |
a33 |
|
|
13 |
|
a31 |
|
a32 |
|
|
|
|||||||||||
Системой двух линейных уравнений с двумя неизвестными х ется система вида
a11x + a12 y = b1, a21x + a22 y = b2 ,
и у называ-
(1.34)
где коэффициенты a11, a12 , a21, a22 и свободные члены b1 и b2 - заданные
числа. Определители
∆ = |
|
a11 |
a12 |
|
, |
∆x = |
|
b1 |
a12 |
|
, |
∆y = |
|
a11 |
b1 |
|
|
|
|
|
|||||||||||
|
|
a21 |
a22 |
|
|
|
|
b2 |
a22 |
|
|
|
|
a21 |
b2 |
называются главным (∆) и побочными (∆x , ∆y ) определителями системы
(1.34).
Если ∆ ≠ 0 , то единственное решение системы (1.34) находится по формулам (правилу) Крамера:
22
|
|
|
|
x = ∆x , |
y = |
∆y |
. |
|
|
|
(1.35) |
|||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
∆ |
|
|
∆ |
|
|
|
|
|
|
|||||||
Системой трех линейных уравнений с тремя |
неизвестными х, у и z |
|||||||||||||||||||||
называется система |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
a11x + a12 y + a13 z = b1, |
|
|
|
|
|
|
||||||||||||||
|
|
a21x + a22 y + a23 z = b2 , |
|
(1.36) |
||||||||||||||||||
|
|
a |
31 |
x + a |
32 |
y + a |
33 |
z = b . |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||
Определители |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a11 |
|
a12 |
a13 |
|
|
|
|
|
|
|
|
|
b1 |
a12 |
a13 |
|
|
||||
|
|
|
|
|
|
|
|
|||||||||||||||
∆ = |
a21 a22 |
a23 |
|
, |
|
|
∆x = |
|
b2 |
a22 |
a23 |
|
, |
|||||||||
|
a31 |
|
a32 |
a33 |
|
|
|
|
|
|
|
|
|
b3 |
a32 |
a33 |
|
|
||||
|
|
a11 |
b1 |
a13 |
|
|
|
|
|
|
|
a11 |
a12 |
b1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
∆y = |
a21 b2 |
a23 |
|
, |
|
|
∆z = |
a21 a22 b2 |
|
. |
||||||||||||
|
|
a31 |
b3 |
a33 |
|
|
|
|
|
|
|
a31 |
a32 |
b3 |
|
|
||||||
называются главным (∆) и побочными (∆x , ∆y , ∆z ) |
определителями системы |
|||||||||||||||||||||
(1.36).
Если ∆ ≠ 0 , то единственное решение системы (1.36) находится по формулам Крамера:
x = |
∆x , |
y = |
∆y |
, |
z = |
∆z |
. |
(1.37) |
∆ |
|
|||||||
|
∆ |
|
|
|
∆ |
|
||
Определители обладают следующими свойствами
1o . Если две строки (два столбца) определителя поменять местами, то знак определителя изменится.
2o . Если две строки (два столбца) определителя равны нулю или пропорциональны, то определитель равен нулю.
3o . Общий множитель элементов строки (столбца) можно вынести за знак определителя.
4o . Если к строке (столбцу) определителя прибавить (поэлементно) линейную комбинацию других строк (столбцов), то величина определителя не изменится.
5o . Если каждый элемент i – й строки (i =1,2,3) определителя равен
сумме двух слагаемых, то такой определитель равен сумме двух определителей, у одного из которых i-я строка составлена из первых слагаемых, у другого – из
23

вторых слагаемых, а в остальных строках те же слагаемые элементы, что и у исходного определителя, т.е., например,
|
|
|
|
a11 |
|
|
|
|
|
|
|
a12 |
|
|
|
|
|
|
|
a13 |
|
|
|
|
|
|
||||
|
|
|
|
a21 |
|
|
|
|
|
|
|
a22 |
|
|
|
|
|
|
|
a23 |
= |
|
|
|||||||
|
|
|
a31 + b31 |
|
a32 + b32 |
|
|
a33 + b33 |
|
|
|
|||||||||||||||||||
|
|
|
|
a11 |
a12 |
a13 |
|
|
|
a11 |
|
a12 |
a13 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
= |
a21 |
a22 |
a23 |
+ |
|
|
a21 |
|
a22 |
a23 |
|
. |
||||||||||||||||||
|
|
|
|
a31 |
a32 |
a33 |
|
|
|
b31 |
|
b32 |
b33 |
|
|
|||||||||||||||
|
|
1.62. Вычислить определитель |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
A |
|
|
|
|
|
2 |
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
= |
|
3 |
|
|
−1 |
2 |
|
. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
||
|
|
∆ По формулам (1.33) и (1.32) имеем: |
||||||||||||||||||||||||||||
A |
|
= 2 |
|
−1 |
2 |
|
−1 |
|
3 |
2 |
|
|
+ 0 |
|
3 |
−1 |
|
|
= 2 (−5 − 6) − (15 −8) = −29. ▲ |
|||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
3 |
5 |
|
|
|
|
|
|
4 |
5 |
|
|
|
|
|
|
4 |
3 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1.63. По формулам Крамера решить систему уравнений:
x + y + 2z = −1, 2x − y + 2z = −4,
4x + y + 4z = −2.
∆ Находим главный и побочные определители системы:
|
|
1 |
1 |
2 |
|
|
|
|
−1 |
1 |
2 |
|
|
|
|
|
|
||||||||||
∆ = |
|
2 |
−1 |
2 |
|
= 6; |
∆x = |
|
− 4 |
−1 |
2 |
|
= 6; |
|
|
4 |
1 |
4 |
|
|
|
|
− 2 |
1 |
4 |
|
|
|
|
1 |
−1 |
2 |
|
|
|
1 |
1 |
−1 |
|
|
|
|
|
|
|
|
|||||||||
∆y = |
|
2 |
− 4 |
2 |
|
=12 ; ∆z = |
|
2 |
−1 |
− 4 |
|
= −12. |
|
|
|
4 |
− 2 |
4 |
|
|
|
4 |
4 |
− 2 |
|
|
|
По формулам (1.37) получаем: x =1, |
y = 2, z = −2. |
▲ |
|||||||||||
1.64. Вычислить определители 2-го порядка:
24
|
|
|
|
|
5 |
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sinα |
cosα |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|||||||||||||
а) |
|
|
|
|
; |
|
|
|
|
|
|
б) |
|
; |
|
|
|
|
|
в) |
|
i |
|
|
; |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
2 |
− 6 |
|
|
cosα |
sinα |
|
|
|
|
|
|
j |
6 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
г) |
|
|
|
sinα |
cosα |
|
; |
д) |
|
a −b |
|
|
|
|
|
|
|
a |
|
|
|
; |
|
е) |
|
am |
|
|
|
a2m |
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
sin β |
cos β |
|
|
a2 |
|
|
a2 + ab + b2 |
|
|
1 |
|
|
|
am |
|
|||||||||||||||||||||||||||||||||||
1.65. Вычислить определители 3-го порядка: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
1 |
−3 2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
5 − 2 |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
−3 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
а) |
|
0 |
|
1 |
1 |
|
|
|
; |
|
б) |
|
0 |
|
2 |
4 |
|
; |
в) |
2 |
3 |
|
1 |
|
; |
|
|
|
|
||||||||||||||||||||||||
|
|
|
2 |
|
0 − 2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
− 2 0 |
|
|
|
|
|
|
|
3 |
1 |
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
1 −1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a −b a −b |
|
|
|
1 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
i |
|
j |
k |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
г) |
|
2 0 4 |
|
; |
|
д) |
1 −1 2 |
; |
|
|
е) |
a −b |
|
1 |
|
|
|
|
|
a +b |
|
; |
|||||||||||||||||||||||||||||||
|
|
|
|
−1 3 2 |
|
|
|
|
|
|
3 2 0 |
|
|
|
|
|
|
1 |
|
|
|
|
a + b a +b |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
sinα |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
ж) |
|
|
|
sin β |
1 |
|
|
|
|
|
|
cos β |
|
; |
|
|
|
|
|
з) |
|
a |
b |
a |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 |
|
|
cosα |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1.66. Решить системы двух уравнений с двумя неизвестными:
3x + 2 y = 7, |
ax −3y =1, |
а) |
б) |
4x −5y = 40. |
ax − 2 y = 2. |
mx − ny = (m − n)2 |
, |
(при m ≠ 2n ). |
|
в) |
2x − y = n |
|
|
|
|
|
|
1.67. С помощью правила Крамера решить системы трех уравнений с тремя неизвестными:
а)
в)
д)
2x −3y + z = 2,x +5y − 4z = −5,
4x + y −3z = −4;
3x + 2y − z = 0,2x − y +3z = 0,
x + y − z = 0;
x + 2y +3z = 5,2x − y − z =1,
x +3y + 4z = 6.
б)
г)
2x − 4y + 3z =1,
x − 2y + 4z = 3,3x − y + 5z = 2;
|
2x − y + z = 2, |
3x + 2y + 2z = −2, |
|
|
x − 2 y + z =1; |
|
|
25

Векторным произведением векторов a и b называется третий вектор c ,
обозначаемый [ a ,b ] и удовлетворяющий следующим условиям:
1o . |
|
|
|
|
= |
|
[ |
|
|
, |
|
] |
|
= |
|
|
|
|
|
|
|
|
|
|
|
sinϕ, |
|
ϕ = ( |
|
,^ |
|
) . |
|
|
|
|
||||||||||||||||
|
c |
|
|
a |
b |
|
|
a |
|
|
|
b |
|
a |
b |
(1.38) |
||||||||||||||||||||||||||||||||||||
2o . |
|
|
|
, |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
c |
a |
c |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
3o . |
|
|
, |
|
и |
|
|
в указанном порядке образуют правую тройку. |
||||||||||||||||||||||||||||||||||||||||||||
Векторы |
a |
b |
c |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
с = [a , b] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это означает, что если начала векторов |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a , b и c совместить, то из конца вектора |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
c кратчайший поворот от |
a |
к |
b |
виден |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
против часовой стрелки (рис. 1.24) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторное произведение обладает |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
следующими свойствами: |
|
|
|||||||||||||||||||||||
1o . |
|
|
|
|
Рис. 1.24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Длина вектора |
|
= [ |
|
, |
|
] |
численно равна площади параллелограмма, |
|||||||||||||||||||||||||||||||||||||||||||||
c |
a |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||
построенного на векторах х a и b , приведенных к общему началу:
S = [a,b] .
2o . Векторное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда они коллинеарны, т.е.
|
|
// |
|
|
|
|
|
|
|
|
[ |
|
|
|
, |
|
|
|
] = 0 - |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
a |
b |
a |
b |
(1.39) |
||||||||||||||||||||||||||||||||||||||
условие коллинеарности двух векторов. |
|
||||||||||||||||||||||||||||||||||||||||||
3o . [ |
|
|
, |
|
|
|
] = −[ |
|
|
, |
|
|
] - |
|
|
|
|
|
|
|
|
(1.40) |
|||||||||||||||||||||
a |
b |
b |
a |
||||||||||||||||||||||||||||||||||||||||
антикоммутативность векторного произведения. |
|
||||||||||||||||||||||||||||||||||||||||||
4o . [λ |
|
|
|
, |
|
|
] = [ |
|
, λ |
|
|
] = λ[ |
|
|
, |
|
|
] - |
(1.41) |
||||||||||||||||||||||||
a |
b |
a |
b |
a |
b |
||||||||||||||||||||||||||||||||||||||
ассоциативность векторного произведения. |
|
||||||||||||||||||||||||||||||||||||||||||
5o . [ |
|
, |
|
+ |
|
] = [ |
|
, |
|
] +[ |
|
, |
|
] - |
(1.42) |
||||||||||||||||||||||||||||
a |
b |
c |
a |
b |
a |
c |
|||||||||||||||||||||||||||||||||||||
дистрибутивность векторного произведения.
A
rA
O
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
Если rA - радиус-вектор точки А, |
|
|
|
||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F = AB - сила, приложенная в точке |
A |
|||||||||||||
|
|
|
||||||||||||||
|
|
(рис. 1.25), то момент этой силы относи- |
||||||||||||||
|
|
тельно точки О выражается формулой |
|
|
||||||||||||
|
|
|
|
|
|
|
|
M |
= [ |
r |
A , |
F |
]. |
(1.43) |
||
Рис. 1.25
Если тело вращается вокруг неподвижной точки О с угловой скоростью ω , то мгновенная линейная скорость v точки М с радиусом-вектором rM определяется вектором
26

v = [ω, r M ].
Если в ДСК a = (x1, y1, z1) , b = (x2 , y2 , z2 ) , то в координатной форме векторное произведение
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i, |
|
j |
k |
|
|
|
|
|
|
|
|
||||||||
|
|
|
[ |
|
, |
|
|
] = |
x1 |
y1 |
z1 |
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
a |
b |
(1.44) |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
y2 |
z2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
Вектор [ |
|
,[ |
|
|
, |
|
|
]] называется |
двойным векторным произведением. Его |
||||||||||||||||||||||||||||||||||||||||
a |
b |
c |
|||||||||||||||||||||||||||||||||||||||||||||||||
можно вычислить по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
[ |
|
,[ |
|
, |
|
]]= |
|
( |
|
, |
|
) − |
|
( |
|
, |
|
) . |
|
|
|
|
|
|
|
|
|
|
|
(1.45) |
|||||||||||||||||||||
a |
b |
c |
b |
a |
c |
c |
a |
b |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
1.68. При каком α векторы |
|
=α |
|
+ 5 |
|
|
|
= 3 |
|
− |
|
коллинеарны, ес- |
|||||||||||||||||||||||||||||||||||||
p |
a |
b |
и |
q |
a |
b |
|||||||||||||||||||||||||||||||||||||||||||||
ли |
a |
и |
|
|
b |
неколлинеарны? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
∆ |
Согласно условию коллинеарности (1.39) и свойствам векторного про- |
||||||||||||||||||||||||||||||||||||||||||||||||
изведения (1.40) – (1.42), имеем: p // q [ p, q] = 0
[αa + 5b,3a −b] = 3α[a, a] +15[b, a] −α[a,b] −5[b,b] =
=15[b, a] +α[b, a] = (15 +α)[b, a] = 0.
Так как |
a |
и |
|
b |
|
неколлинеарны, то это равенство возможно, если |
|||||||||||||
15 +α = 0 α = −15 . |
Итак, векторы |
p |
и |
|
|
q |
будут коллинеарны при |
||||||||||||
α = −15. |
|
|
|
|
|
|
|
|
|
|
▲ |
||||||||
1.69. Вычислить площадь параллелограмма, три вершины которого нахо- |
|||||||||||||||||||
дятся в точках A = (4,3,2), B = (2,3,4), |
|
C = (1,1,1). |
|||||||||||||||||
∆ Образуем векторы |
|
= |
|
= (−2,0,2) |
и |
|
= |
|
= (−3,−2,−1). Тогда |
||||||||||
a |
AB |
b |
AC |
||||||||||||||||
искомая площадь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
i |
j |
k |
|
|
|
|
|
|
|
|
|
||||||
s = [a,b] = − 2 0 |
2 = 4i −8 j + 4k = 16 + 64 +16 = 4 6 . ▲ |
||||||||||||||||||
|
−3 |
− 2 |
−1 |
|
|
|
|
|
|
|
|
|
|||||||
1.70. Три силы F1 = (2,−1,−3), F 2 = (3,2,−1), F 3 = (−4,1,3) прило-
жены к точке B = (−1,4,−2). Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки A = (2,3,−1) .
∆ Находим равнодействующую трех сил F = F1 + F 2 + F 3 = (1,2,−1).
27

Искомый момент M = [AB, F]. Так как AB = (−3,1,−1), то
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
j |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
= |
−3 1 −1 |
= |
|
|
|
|
− 4 |
|
|
−7 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
M |
i |
j |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
Величина этого момента M = 66 , а направляющие косинусы: |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
cosα = M x |
= 1 |
|
66 |
, |
|
|
|
|
|
|
cos β = |
M y |
= − 4 |
66 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
cosγ = M z |
= − 7 |
66 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
▲ |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1.71. |
Найти координаты двойного векторного произведения [ |
|
|
,[ |
|
|
|
, |
|
|
|
]], ес- |
||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
c |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ли |
|
|
|
= (2,−3,1), |
|
= (−3,1,2), |
|
|
|
|
= (1,2,3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
a |
b |
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
∆ |
|
Воспользуемся |
|
формулой |
(1.45). |
Имеем: ( |
|
|
, |
|
|
) = −1, |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
a |
c |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
( |
|
, |
|
) = (3,−1,−2) ; |
( |
|
, |
|
) = −7, |
|
( |
|
, |
|
) = (−7,−14,−21) . Тогда [ |
|
,[ |
|
, |
|
]]= |
|||||||||||||||||||||||||||||||||||
|
b |
a |
c |
a |
b |
c |
a |
b |
a |
b |
c |
|||||||||||||||||||||||||||||||||||||||||||||||
= (3,−1,−2) −(−7,−14,−21) = (10,13,19) . |
|
|
|
|
|
|
|
|
|
|
|
|
▲ |
|||||||||||||||||||||||||||||||||||||||||||||
1.72.Доказать тождество [a,b]2 + (a,b)2 = a b 2 .
1.73.Найти координаты векторного произведения [2a + b,b], если
|
= (3,−1,−2), |
|
|
= (1,2,−1). |
||
a |
b |
|||||
|
1.74. Показать, что момент силы |
|
= (−3,1,−1) , приложенной к точке |
|||
|
F |
|||||
A = (4,−2,3), |
относительно точки B = (7,3,−1) , не является вектором, |
|||||
перпендикулярным к вектору a = (1,1,2) .
1.75. Проверив, что векторы a = (1,0,−1), b = (−1,1,0), c = (2,0,−3)
некомпланарны, найти единичный вектор d , ортогональный векторам a и b . 1.76. Найти площадь параллелограмма, построенного на векторах
|
|
|
|
= (−1,3), |
|
|
|
|
|
= (1,2) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
a |
b |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
1.77. |
|
|
|
Вычислить площадь треугольника с вершинами |
в точках |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A = (−1,0,−1) , B = (0,2,−3), C = (4,4,1) . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Выразить векторы 1) [ |
|
+ |
|
, |
|
− |
|
] |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
1.78. Даны векторы |
a |
и |
b |
a |
b |
a |
b |
и |
||||||||||||||||||||||||||||||||||||||||||
2) [( |
|
|
+ |
|
|
) / 2, |
|
− |
|
|
/ 2]через вектор |
|
|
= [ |
|
|
, |
|
]. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
a |
b |
b |
a |
c |
a |
b |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
, |
|
|
|
= [ |
|
, |
|
], |
|||||||||||||||||||||||||||||
1.79. |
|
Три ненулевых вектора |
a |
b |
c |
связаны соотношениями |
a |
b |
c |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
= [ |
|
, |
|
], |
|
|
= [ |
|
, |
|
]. Найти длины этих векторов и угол ϕ между ними. |
||||||||||||||||||||||||||||||||||||||||||
b |
c |
a |
c |
a |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||
28

|
|
1.80 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по |
|
||||||||
|
|
|
|
Даны |
|
разложения |
векторов |
a |
и |
b |
базису |
|||||||||||||||||||||||||
{e |
1, |
|
2 , |
|
|
3 }: |
|
|
|
= (ax , ay , az ), |
|
|
= (bx ,by ,bz ). Разложить вектор [ |
|
, |
|
] |
|
||||||||||||||||||
e |
e |
a |
b |
a |
b |
по век- |
||||||||||||||||||||||||||||||
торам |
|
1 =[ |
|
2 , |
|
3 ], |
|
2 =[ |
|
3 , |
|
1], |
|
3 =[ |
|
1, |
|
2 ]. |
|
|
|
|
|
|
|
|||||||||||
c |
e |
e |
c |
e |
e |
c |
e |
e |
|
|
|
|
|
|
|
|||||||||||||||||||||
1.81.Найти синус угла ϕ между диагоналями параллелограмма, построенного на векторах a = (2,1,−1), b = (1,−3,1).
1.82.Найти синус угла ϕ вектора c = (1,3,1) с плоскостью, порождаемой векторами a = (2,−1,3) и b = (1,0,1) .
1.83.Вектор c , перпендикулярный к оси Z и к вектору a = (8,−15,3), образует острый угол с осью Х. Зная, что c = 51, найти его координаты.
1.84.Доказать, что площадь S треугольника , векторы сторон которого равны векторам медиан треугольника АВС составляет 3 / 4 площади δ треугольника АВС.
1.85 . Дан треугольник АВС. На прямых (АВ), (ВС), (СА) выбраны соот-
ветственно точки M, N, P так, что |
|
|
|
|
|
|
|
|
=α |
|
|
|
|
|
=α |
|
|
|
|
|
|
|
, . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
AM |
AB, |
BN |
BC |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
=α |
|
|
|
|
|
|
|
. При каком значении α площадь S(α) треугольника, векторы |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
CP |
CA |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
сторон которого |
CM |
|
AN |
BP |
|
наименьшая ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1.86. Вычислить [[ |
|
|
|
|
|
, |
|
], |
|
|
|
], если |
|
|
|
= (2,−3,1), |
|
|
= (−3,1,2) и |
|
|
= (1,2,3) . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a |
b |
c |
a |
|
b |
c |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1.87 . При каком необходимом и достаточном условии справедливо равен- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ство [[ |
|
|
|
, |
|
|
], |
|
|
]= [ |
|
|
|
,[ |
|
|
, |
|
|
|
]]? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
a |
b |
c |
a |
b |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1.88. Проверить справедливость равенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
[[ |
|
, |
|
], |
|
]+ [[ |
|
, |
|
|
], |
|
|
|
]+ [[ |
|
, |
|
|
], |
|
|
]= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
a |
b |
c |
b |
c |
a |
c |
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.4. Смешанное произведение векторов. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
, |
|
, |
|
) трех векторов |
|
|
, |
|
|
, |
|
|
|
|
|
называется |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Смешанным произведением |
a |
b |
c |
a |
b |
c |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
число |
( |
|
|
|
, |
|
|
|
, |
|
|
|
) = ([ |
|
|
|
|
, |
|
|
], |
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.46) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
c |
a |
b |
c |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Смешанное произведение обладает |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
свойствами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1o . Смешанное произведение ( |
|
|
, |
|
, |
|
) |
|||||||||||||||||||||||||||||||
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
c |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равно объему v ориентированного |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
параллелепипеда, построенного на |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
приведенных к общему началу не- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
и |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V > 0 |
|
компланарных векторах |
a |
b |
c |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис.1.26). Это означает, что v > 0, если |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
29

тройка векторов a,b и c правая, и v < 0, если эта тройка левая.
2o . Смешанное произведение векторов a,b и c равно нулю, если эти векторы компланарны. Другими словами, равенство
( |
|
|
|
, |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
) = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.47) |
|||||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
является условием компланарности трех векторов. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3o . Если в правом ортонормированном базисе { |
|
, |
|
|
|
, |
|
|
} |
|
|
= (ax , ay , az ) , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i |
j |
k |
a |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
= (bx ,by ,bz ), |
|
|
= (cx ,cy ,cz ) , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax |
|
|
|
|
|
ay |
|
|
|
|
|
|
az |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
( |
|
|
|
, |
|
|
|
, |
|
|
) = |
|
|
bx |
|
|
|
|
|
by |
|
|
|
|
|
|
bz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
a |
b |
c |
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.48) |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cx |
|
|
|
|
|
cy |
|
|
|
|
|
|
cz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
координатная форма смешанного произведения. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4o . Базис { |
|
, |
|
|
|
|
, |
|
|
|
|
|
} |
|
является |
правым тогда и только тогда, когда |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
b |
c |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
( |
|
|
, |
|
, |
|
) > 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
a |
b |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
5o . ( |
|
|
, |
|
|
, |
|
|
|
) = ( |
|
, |
|
|
|
, |
|
) = ( |
|
|
, |
|
|
|
, |
|
|
) = −( |
|
|
, |
|
, |
|
|
) = −( |
|
, |
|
|
, |
|
) = −( |
|
, |
|
, |
|
). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
b |
c |
b |
c |
a |
c |
a |
b |
a |
c |
b |
c |
b |
a |
b |
a |
c |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
6o . Если |
|
|
= ax |
|
|
1 + ay |
|
2 + az |
|
3 , |
|
= bx |
|
1 + by |
|
2 + bz |
|
3 , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
e |
e |
e |
b |
e |
e |
e |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
= cx |
|
|
1 + cy |
|
2 + cz |
|
3 , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
c |
e |
e |
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax |
|
|
|
|
ay |
|
az |
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(a,b,c) = |
b |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
,e |
(1.49) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
y |
|
z |
|
e ,e |
|
|
|
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cx |
|
|
|
|
cy |
|
cz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
7o . Смешанное произведение линейно по каждому из сомножителей:
(λa + µd,b, c) = λ(a,b, c) + µ(d,b, c) , (a,λb + µd,c) = λ(a,b, c) + µ(a, d, c), (a,b, λc + µd) = λ(a,b, c) + µ(a,b, d) .
8o . |
D |
|
Объем тетраэдра, построенного на трех |
|
C |
||
c |
|
некомпланарных векторах как на ребрах, |
|
h |
b |
приведенных к общему началу А, равен |
|
|
|
|
(1/6)-й модуля смешанного произведения |
A |
|
|
этих векторов (рис. 1.27). |
|
|
|
|
|
a |
B |
|
|
Рис. 1.27 |
|
|
30

1.89. |
|
|
|
|
Даны вершины тетраэдра A = (0,0,2) , |
|
B = (3,0,5), |
C = (1,1,0), |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
D = (4,1,2) . Найти его объем и длину высоты h, |
опущенной из вершины D. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(рис. 1.27). |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
∆ Имеем v = |
|
|
( |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
= |
|
Sосн h . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
AB |
AC |
AD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Sосн |
= |
|
1 |
|
|
|
[ |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
] |
|
|
h |
= |
|
( |
|
|
AB |
, AC, |
AD |
) |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
AB |
|
|
AC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[AB, AC] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Так как |
|
|
|
|
= (3,0,3), |
|
|
|
|
|
|
|
|
|
|
|
|
= (1,1,−2) |
|
|
|
|
|
|
|
|
= (4,1,0) , то |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
AB |
AC |
|
AD |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
[AB, AC] = mod 3 |
0 |
|
|
|
|
|
|
|
|
3 = −3i +9 j +3k = 3 41; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
( |
|
|
|
, |
|
|
|
, |
|
|
|
) |
|
= |
|
( |
|
,[ |
|
|
|
|
|
|
|
, |
|
|
|
]) |
|
= |
|
|
4 (−3) +1 9 + 0 3 |
|
= |
|
|
|
−3 |
|
= 3. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
AB |
|
AC |
AD |
|
|
AD |
|
AB |
|
AC |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Значит, h = 3/ 3 11 =1/ |
11 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
▲ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Докажите, что если [ |
|
|
, |
|
|
] +[ |
|
, |
|
] +[ |
|
, |
|
] = |
|
|
|
, то векторы |
|
|
, |
|
, |
|
|
|
ком- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1.90. |
|
|
a |
b |
b |
c |
c |
a |
0 |
a |
b |
c |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
планарны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≠ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
∆ |
|
|
Умножая |
|
|
|
|
данное |
|
|
|
|
равенство |
скалярно на |
|
|
|
|
, |
|
|
|
|
|
получаем |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
0 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 = ( |
a |
,[ |
a |
, |
b |
]) + ( |
a |
,[ |
b |
, |
c |
]) + ( |
a |
[ |
c |
, |
a |
]). Так |
как ( |
a |
,[ |
a |
, |
b |
]) = [ |
a |
,[ |
c |
, |
a |
]) = |
0 |
по |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
свойству смешанного произведения, то (a,b, c) = 0, что и означает компланарность этих векторов. ▲
1.91. Доказать, что если векторы [a,b],[b, c],[c, a] компланарны, то они коллинеарны.
1.92 . Доказать тождество
[[a,b],[c, d]]= c(a,b, d) − d(a,b, c).
1.93 . Доказать, что
([a,b],[b, c],[c, d ])= (a,b, c)2 .
1.94. Определить ориентацию тройки векторов a = i + j , b = i − j ,
c = k .
1.95.Образуют ли векторы a = (2,3,−1), b = (1,−1,3) , c = (1,9,−11) ба-
зис в R3 ?
1.96.Доказать тождество (a + c,b, a + b) = −(a,b,c).
1.97.Доказать, что для любых векторов a,b,c векторы
31

a −b, b − c, c − a компланарны. Каков геометрический смысл этого факта? 1.98. Компланарны ли векторы a = (5,−1,4),b = (2,3,−1),c = (4,3,2)? 1.99. Лежат ли точки A = (3,1,4), B = (−1,1,6), C = (5,2,2),
D = (−1,6,1) в одной плоскости?
1.100. При каком α компланарны векторы
a = (1,−2,1), b = (7,α,−13), c = (3,1,−2)?
1.101. Доказать, что объем параллелепипеда, построенного на диагоналях граней данного параллелепипеда, равен удвоенному объему данного параллелепипеда.
1.102. Найти вектор c, c =13, ортогональный векторам a = (1,4,0) , b = (1,0,3) и направленный так, что упорядоченная тройка a,b,c - правая.
1.103 . Найти вектор x , образующий с данными векторами a,b,c равные углы.
32
