ТЭЦ - AC / 05 Лекция - Part 3 Комплексный метод расчета электрических цепей

Комплексный (символический) метод расчета электрических цепей при периодическом синусоидальном воздействии

Напомним, что, как было показано в предыдущей лекции, напряжения, токи и сопротивления (проводимости) в цепях переменного тока можно представить комплексными числами.

Поскольку в электротехнике, т.к. буква i изображает ток, за признак мнимости принята буква j, а комплексная величина обозначается либо точкой сверху , либо подчеркиванием снизу (редко), либо выделяется жирным шрифтом A).

;

А – модуль;

– аргумент или фаза.

Н апомним еще раз, что вектор А на комплексной плоскости вращается против часовой стрелки с угловой скоростью ω, то это комплексное число запишется:

Величину назвали оператором вращения.

Можно видеть, что мгновенное значение периодического синусоидального тока и напряжения , определяется мнимой частью вращающегося комплексного числа, т.е. можно утверждать:

,

.

Комплексное число назвали комплексной амплитудой тока, а – комплексном действующего значения тока.

Комплексное число назвали комплексной амплитудой напряжения, – комплексом действующего значения напряжения (как мы помним , ).

Из этих выражений видно, что мгновенное значение периодического синусоидального тока и напряжения есть мнимая часть произведения комплексной амплитуды тока или напряжения на оператор вращения .

Например, если даны ток или напряжение как функции времени, для них можно записать соответствующие комплексные амплитуды (для заданной частоты):

, , (А).

, ; (В).

Если же даны комплексные ток или напряжение, для них можно записать соответствующие ток или напряжение как функции времени (если известна частота):

, (А).

, , (В).

Рассмотрим далее расчеты некоторых простых цепей.

Последовательное соединение R и L

Последовательно соединенные элементы R и L называются RL-цепью. Рассмотрим расчет этой цепи.

Пусть на цепь воздействует синусоидальное (гармоническое) напряжение с нулевой начальной фазой:

. Требуется найти ток в цепи i(t).

Запишем выражение для комплексной амплитуды напряжения. Для заданной частоты ω комплексная амплитуда напряжения будет выглядеть: .

Вычислим полное электрическое сопротивление цепи:

.

Переходя к показательной форме записи, имеем:

, где

Зная полное электрическое сопротивление (импеданс), можно найти ток в цепи:

.

Далее перейдем назад к форме записи тока во временной области:

i(t) = I_msin(ωt +(0-φ))

Выполним все эти вычисления с численными данными. (…)

f = 50 Гц; U = 220 В, R = 100 Ом; L = 0,32 Гн.

Последовательное соединение R и C

Последовательно соединенные элементы R и C называются RC-цепью. Рассмотрим расчет этой цепи.

Пусть на цепь воздействует синусоидальное (гармоническое) напряжение с нулевой начальной фазой:

. Требуется найти ток в цепи i(t).

Запишем выражение для комплексной амплитуды напряжения. Для заданной частоты ω комплексная амплитуда напряжения будет выглядеть: .

Вычислим полное электрическое сопротивление цепи:

.

Переходя к показательной форме записи, имеем:

, где

Зная полное электрическое сопротивление (импеданс), можно найти ток в цепи:

.

Изобразим векторную диаграмму. Проанализируем фазовые соотношения в цепи. Выражение выше трактуют как «треугольник сопротивлений».

Далее перейдем назад к форме записи тока во временной области:

i(t) = I_msin(ωt +(0-φ))

Выполним все эти вычисления с численными данными. (…)

f = 1 кГц; U = 220 В, R = 510 Ом; C = 0,5 мкФ.

Последовательное соединение R, L, C.

В соответствии с законом Кирхгофа для напряжений можно записать:

, (1)

где ток и напряжения являются гармоническими функциями времени.

Перейдем к комплексной форме записи (1), аналогично тому, как это делалось ранее:

. (2)

Уравнение (2) можно записать:

,

где

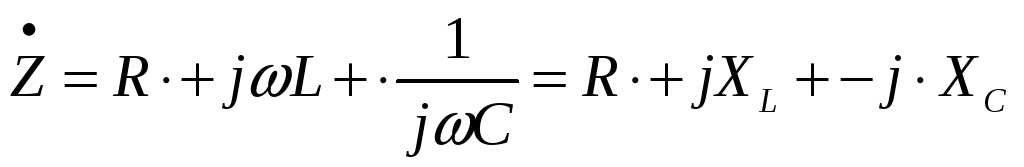
где – комплексное сопротивление, или полное электрическое сопротивление, или импеданс (impedance);

–комплексное индуктивное сопротивление,

–комплексное емкостное сопротивление,

–комплексное реактивное сопротивление (reactance).

Если реактивное сопротивление X (reactance) равно нулю, то полное электрическое сопротивление, или импеданс (impedance) превращается только в активное сопротивление (resistance) и цепь становится чисто активной, или резистивной, или превращается в цепь постоянного тока.

Следует помнить: , , , , .

,

Комплексное число всегда можно представить в виде вектора на комплексной плоскости. Диаграмма, отражающая совокупность векторов токов и напряжений с учетом их фаз на комплексной плоскости называется векторной диаграммой (она широко используется при расчетах).

Для данной схемы:

,

(надо помнить, что )

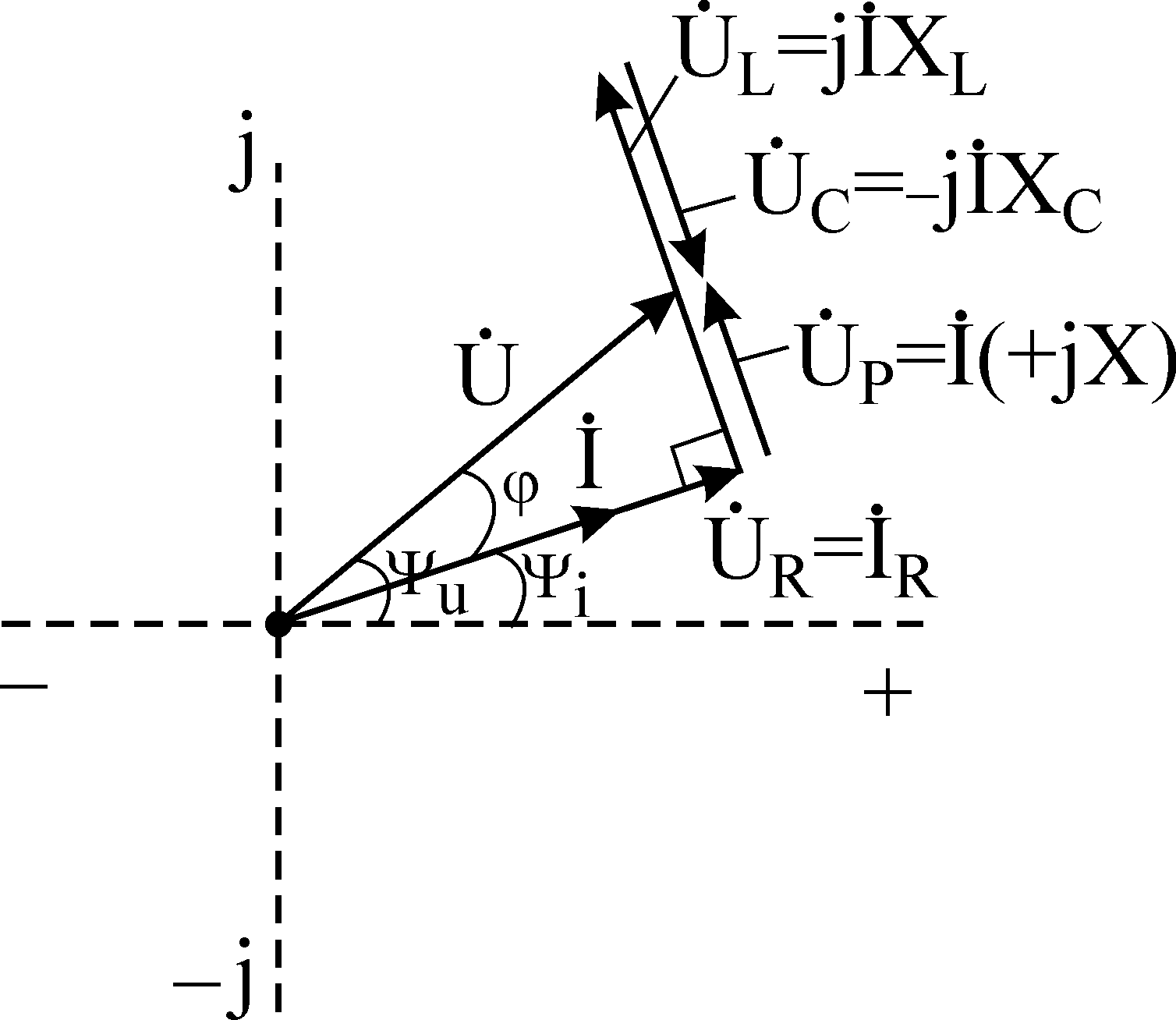
Проанализируем векторные диаграммы. Характер сопротивления цепи зависит от соотношения индуктивного и емкостного сопротилвний.

При X_L>X_C сдвиг фаз между приложенным к цепи напряжением и током в цепи положителен, т.е. φ>0 (см. левый рисунок). Ток в цепи отстает по фазе от приложенного напряжения и, следовательно, цепь имеет индуктивный характер.

При X_L<X_C сдвиг фаз между приложенным к цепи напряжением и током в цепи отрицателен, т.е. φ<0 (см. правый рисунок). Ток в цепи опережает по фазе приложенное напряжения и, следовательно, цепь имеет емкостной характер.

Параллельное соединение R, L, С.

В соответствии с законом Кирхгофа для токов можно записать:

(3)

где токи и напряжение являются гармоническими функциями времени.

Перейдем к комплексной форме записи (1), аналогично тому, как это делалось ранее:

(4)

Уравнение (4) можно записать:

,

где

– комплексная проводимость, или полная электрическая проводимость admittance);

– комплексная индуктивная проводимость;

– комплексная емкостная проводимость;

– комплексная реактивная проводимость (susceptance).

Связь между комплексными сопротивлениями и проводимостями:

;

;

;

Изобразим векторную диаграмму. – Случаи, когда цепь носит индуктивный характер и емкостной характер.

Комплексная мощность

За комплексную мощность приняли произведение комплекса действующего значения напряжения на сопряженный комплекс действующего значения тока (сопряженный комплекс изменен на обратный () знак прямого комплексного числа (, )).

Если , , тогда учитывая известные ранее полную мощность , активную мощность , реактивную мощность , имеем:

В электрических цепях при периодическом синусоидальном воздействии имеет место баланс мощностей источников и нагрузок, т.е. комплексная мощность источников энергии должна быть ровна комплексной мощности нагрузок и активные и реактивные мощности источников равны активной и реактивной мощностям нагрузок.

,

, ,

, .

Знак реактивной мощности означает преимущество индуктивного (+) или емкостного (–) сопротивлений.