Лекции_2 / 17 Примеры к 4.2 и 4.3 ПЗ

10

4.2. Кольцо полиномов и его свойства

№1. Найти НОД полиномов.

а) f(x) = x³+x²+2x+2, g(x) = x²+x+1 над Z/3Z и над Q.

Ответ: и 1 соответственно.

б)  над Z/5Z и над Q.

Ответ: и соответственно.

№2. Разложить полином на неприводимые множители над полем.

а) над Z/2Z.

Ответ: .

б) над Z/3Z.

Ответ:

№3. Разложить полиномы на неприводимые множители над полем.

а) Все полиномы второй степени от х над Z/2Z (F₂).

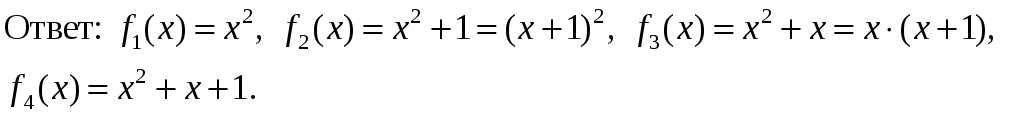
б) Все полиномы третьей степени от х над Z/2Z (F₂).

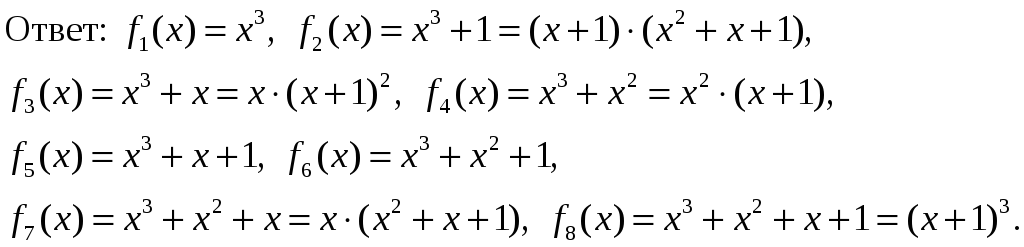
№4. Максимален ли идеал в кольце полиномов?

Решение (см на след. стр.):

В то же время, неприводим над . Если бы был приводим над , то разложение было бы другим и над R, чего быть не может. Каноническое разложение на неприводимые множители со старшим коэффициентом 1 определяется однозначно.

не является максимальным идеалом в R[x] и C[x], но является максимальным идеалом в [x].

Ответ: не максимальный идеал в R[x] и C[x], максимальный идеал в [x].

Решение:

.

– единственный неприводимый многочлен 2-ой степени в .

f(x).

Неприводимыми многочленами степени 3 над являются .

x3 + x + 1f(x).

.

Значит, неприводим над Z/2Z,  <f(x)> максимален в Z/2Z[x] (и  – поле).

Ответ: максимальный идеал.

Решение:

Ответ: не максимальный идеал.

Решение:

Ответ: не максимальный идеал.

Решение:

Если полином третьей степени приводим над полем, то среди его делителей будет хотя бы один полином первой степени.

x³+x+1 не имеет корней в Z/2Z, поэтому он неприводим над Z/2Z, следовательно, <x³+x+1> – максимальный идеал в Z/2Z[x].

Известно утверждение: если многочлен f(x) с целыми коэффициентами и со старшим коэффициентом, равным 1, имеет корни в Q, то все корни целые и являются делителями свободного члена.

Ответ: максимальный идеал.

Решение:

3 – простое число,

Ответ: максимальный идеал.

4.3. Факторкольца. Конечные поля. Гомоморфизмы колец

№1. Построить факторкольцо Р[x]/<f(x)>. Является ли оно полем? В случае положительного ответа найти характеристику поля.

а) .

Решение:

= неприводим над – поле. Это конечное поле из 2 элементов характеристики 2. Сложение и умножение в данном поле задаются таблицами Кэли (таблицы 4.2.1 и 4.2.2 соответственно).

Таблица 4.2.1

Обозначим корень полинома f(x), тогда выполняется соотношение . Откуда находим выражения степеней элемента .

,

,

,

,

.

Таблица 4.2.2

	0:	1:	:	:
0:
1:
:
:

Замечание. В данном случае является так называемым примитивным элементом поля , его степенями исчерпываются все ненулевые элементы данного поля. Так получается потому, что степени , , …, различны. Но в общем случае это неверно для произвольного корня неприводимого полинома над конечным полем. Если не является примитивным элементом, то в качестве примитивного элемента нужно брать подходящую линейную комбинацию степеней элементов .

Ответ: поле из 8 элементов характеристики 2.

б) .

Решение:

= не имеет корней в – конечное поле из элементов характеристики 3. Сложение и умножение в данном поле задаются таблицами Кэли (таблицы 4.2.3 и 4.2.4 соответственно).

Таблица 4.2.3