Глава IV. Элементы теории колец и полей §4.1. Кольца, их основные типы и свойства

Определение 4.1.1. Кольцо (K, +, ) – это алгебраическая система с непустым множеством K и двумя бинарными алгебраическими операциями на нем, которые будем называть сложением и умножением. Кольцо является абелевой аддитивной группой, а умножение и сложение связаны законами дистрибутивности: (a + b)  c = a  c + b  c и с  (a + b) = c  a + c  b для произвольных a, b, c  K.

Пример 4.1.1. Приведем примеры колец.

1. (Z, +, ), (Q, +, ), (R, +, ), (C, +, ) – соответственно кольца целых, рациональных, вещественных и комплексных чисел с обычными операциями сложения и умножения. Данные кольца называются числовыми.

2. (Z/nZ, +, ) – кольцо классов вычетов по модулю n  N с операциями сложения и умножения.

3. Множество M_n(K) всех квадратных матриц фиксированного порядка n  N с коэффициентами из кольца (K, +, ) с операциями матричного сложения и умножения. В частности, K может быть равно Z, Q, R, C или Z/nZ при n  N.

4. Множество всех вещественных функций, определенных на фиксированном интервале (a; b) вещественной числовой оси, с обычными операциями сложения и умножения функций.

5. Множество полиномов (многочленов) K[x] с коэффициентами из кольца (K, +, ) от одной переменной x с естественными операциями сложения и умножения полиномов. В частности, кольца полиномов Z[x], Q[x], R[x], C[x], Z/nZ[x] при n  N.

6. Кольцо векторов (V₃(R), +, ) c операциями сложения и векторного умножения.

7. Кольцо ({0}, +, ) с операциями сложения и умножения: 0 + 0 = 0, 0  0 = = 0.

Определение 4.1.2. Различают конечные и бесконечные кольца (по числу элементов множества K), но основная классификация ведется по свойствам умножения. Различают ассоциативные кольца, когда операция умножения ассоциативна (пункты 1–5, 7 примера 4.1.1) и неассоциативные кольца (пункт 6 примера 4.1.1: здесь , ). Ассоциативные кольца делятся на кольца с единицей (есть нейтральный элемент относительно умножения) и без единицы, коммутативные (операция умножения коммутативна) и некоммутативные.

Теорема 4.1.1. Пусть (K, +, ) – ассоциативное кольцо с единицей. Тогда множество K ^* обратимых относительно умножения элементов кольца K – мультипликативная группа.

Проверим выполнение определения группы 3.2.1. Пусть a, b  K ^*. Покажем, что a  b  K ^*.  (a  b)^–1 = b^–1  а^–1  K. Действительно,

(a  b)  (b^–1  а^–1) = a  (b  b^–1)  а^–1 = a  1  а^–1 = 1,

(b^–1  а^–1)  (a  b) = b^–1  (а^–1  a)  b = b^–1  1  b = 1,

где а^–1, b^–1  K – обратные элементы к a и b соответственно.

1) Умножение в K ^* ассоциативно, так как K – ассоциативное кольцо.

2) 1^–1 = 1: 1  1 = 1  1  K ^*, 1 – нейтральный элемент относительно умножения в K ^*.

3) Для  a  K ^*, а^–1  K ^*, так как (а^–1)  a = a  (а^–1) = 1 (а^–1)^–1 = a.

Определение 4.1.3. Множество K ^* обратимых относительно умножения элементов кольца (K, +, ) называют мультипликативной группой кольца.

Пример 4.1.2. Приведем примеры мультипликативных групп различных колец.

1. Z^* = {1, –1}.

2. M_n(Q)^* = GL_n(Q), M_n(R)^* = GL_n(R), M_n(C)^* = GL_n(C).

3. Z/nZ^* – множество обратимых классов вычетов, Z/nZ^* = { | (k, n) = 1, 0  k < n}, при n > 1 | Z/nZ^* | = (n), где  – функция Эйлера.

4. {0}^* = {0}, так как в данном случае 1 = 0.

Определение 4.1.4. Если в ассоциативном кольце (K, +, ) с единицей группа K ^* = K\{0}, где 0 – нейтральный элемент относительно сложения, то такое кольцо называют телом или алгеброй с делением. Коммутативное тело называется полем.

Из данного определения очевидно, что в теле K ^*   и 1  K ^*, значит, 1  0, поэтому минимальное тело, являющееся полем, состоит из двух элементов: 0 и 1.

Пример 4.1.3.

1. (Q, +, ), (R, +, ), (C, +, ) – соответственно числовые поля рациональных, вещественных и комплексных чисел.

2. (Z/pZ, +, ) – конечное поле из p элементов, если p – простое число. Например, (Z/2Z, +, ) – минимальное поле из двух элементов.

3. Некоммутативным телом является тело кватернионов – совокупность кватернионов, то есть выражений вида h = a + bi + cj + dk, где a, b, c, d  R, i² = = j² = k² = –1, i  j = k = – j  i, j  k = i = – k  j, i  k = – j = – k  i, с операциями сложения и умножения. Кватернионы складываются и перемножаются почленно с учетом указанных выше формул. Для всякого h  0 обратный кватернион имеет вид: .

Различают кольца с делителями нуля и кольца без делителей нуля.

Определение 4.1.5. Если в кольце найдутся ненулевые элементы a и b такие, что a  b = 0, то их называют делителями нуля, а само кольцо – кольцом с делителями нуля. В противном случае кольцо называется кольцом без делителей нуля.

Пример 4.1.4.

1. Кольца (Z, +, ), (Q, +, ), (R, +, ), (C, +, ) – кольца без делителей нуля.

2. В кольце (V₃(R), +, ) каждый отличный от нуля элемент является делителем нуля, поскольку для всех V₃(R).

3. В кольце матриц M₃(Z) примерами делителей нуля являются матрицы 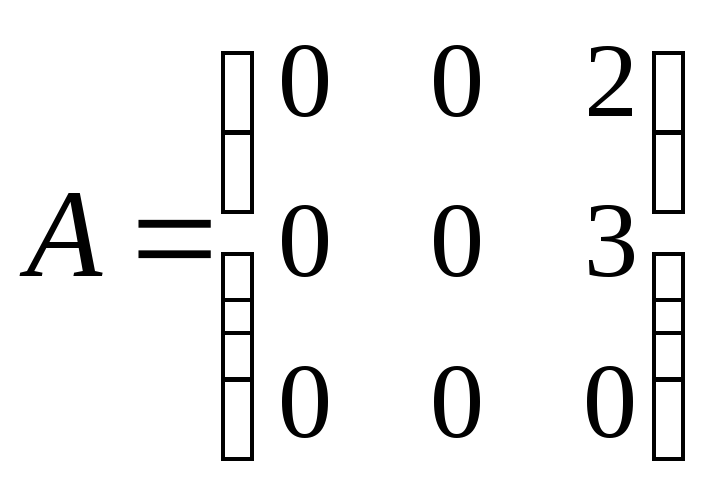и 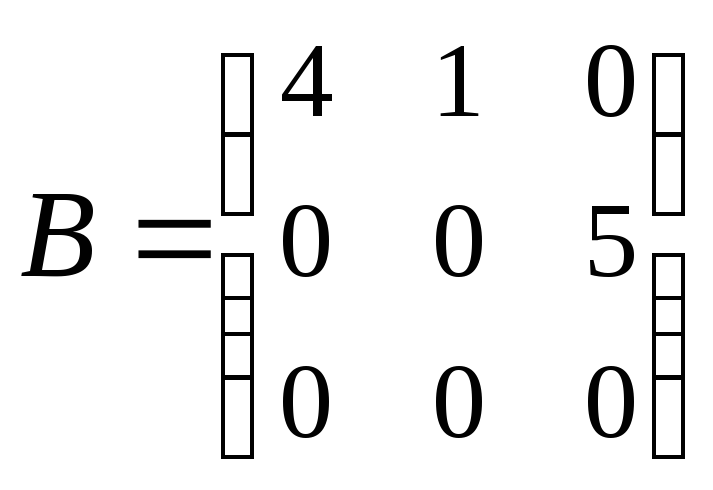, так как A  B = O (нулевая матрица).

4. В кольце (Z/nZ, +, ) с составным n = k  m, где 1 < k, m < n, классы вычетов и являются делителями нуля, так как .

Ниже приведем основные свойства колец и полей.