Лекции_2 / 07 Примеры к 2

§2.2. Взаимно однозначное соответствие. Мощность множества. Счетные, несчетные, континуальные множества и их свойства

Пример 2.2.1. Доказать, что множество N² счетно.

Решение.

N² = {(m, n) | m, n  N}. Разобьем N² на классы. К первому классу N₂ отнесем все пары чисел с минимальной суммой, равной 2. Таким образом, N₂ = {(1, 1)}. Ко второму классу N₃ отнесем все пары чисел с суммой 3: N₃ = {(1, 2), (2, 1)}. Тогда N₄ = {(1, 3), (2, 2), (3, 1)}. В общем случае N_i = {(1, i –– 1), (2, i – 2), (3, i – 3),…, (i – 1, 1)}, i = 2, 3,… Каждый класс содержит ровно i – 1 пару. Упорядочим классы по возрастанию индексов i, а пары внутри класса – по возрастанию первого элемента и занумеруем получившуюся последовательность пар номерами 1, 2, 3,… Легко видеть, что если m + n = i + 1, то пара (m, n) получит номер 0 + 1 + 2 + … + (i – 1) + m = . Эта нумерация задает взаимно однозначное соответствие N²  N и доказывает счетность N².

Пример 2.2.2. Доказать, что бесконечное множество равносторонних треугольников, в котором вершинами каждого треугольника являются середины сторон уже построенного треугольника (рис. 2.2.1), является счетным.

Рис. 2.2.1

Решение.

Докажем, что это бесконечное множество равносторонних треугольников является счетным. Каждому равностороннему треугольнику поставим в соответствие длину его стороны. Если длина стороны фиксированного треугольника равна b, то длина стороны предыдущего треугольника равна 2b, а последующего – b/2. Итак, существует взаимно однозначное соответствие между данным бесконечным множеством равносторонних треугольников и множеством чисел Т_b = {2ⁿb | n  Z}. Покажем, что T_b  N.

f задает взаимно однозначное соответствие между множествами T_b и N. Следовательно, рассмотренное бесконечное множество равносторонних треугольников является счетным.

Пример 2.2.3. Показать, что множество всех вещественных чисел интервала (0; +) – континуальное множество.

Решение.

Известно, что R – континуальное множество. Рассмотрим соответствие f: R  (0; +), f(x) = e^x,  x  R. Тогда для  у  (0; +) существует единственное х  R, такое что f(x) = y, x = ln y. Итак, R  (0; +).

Пример 2.2.4. Доказать, что множество точек гиперболы у = 1/х на действительной плоскости имеет мощность континуум.

Решение.

Представим множество точек гиперболы в следующем виде: Г = {(x, 1/x) | x  R\{0}}. Установим взаимно однозначное соответствие между множествами Г и R.

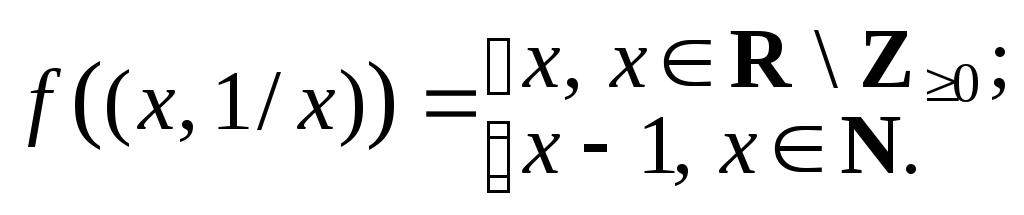
f: Г  R действительно является взаимно однозначным соответствием (рис. 2.2.2). Итак, Г  R. Поскольку R – континуальное множество, Г – также континуальное множество.

Рис. 2.2.2

Пример 2.2.5. Доказать равномощность С\{0} и (0; +)  (–2 ; ).

Решение.

(–2 ; )  (0; 2): f(x) = , f – биекция.

(0; 2)  [0; 2): g – биекция.

(–2 ; )  [0; 2): gf – биекция,

(0; +∞)  (–2 ; )  (0; +∞)  [0; 2): ((x, y)) = (gf(x), y), – биекция.

h(z) = h(e^i) = (, ),   (0; +),    [0; 2), – показательная форма записи комплексного числа.

h – биекция С\{0} на (0; +∞)  [0; 2).

Таким образом, (0; +∞)  (–2 ; )  С\{0}, поскольку – биекция.