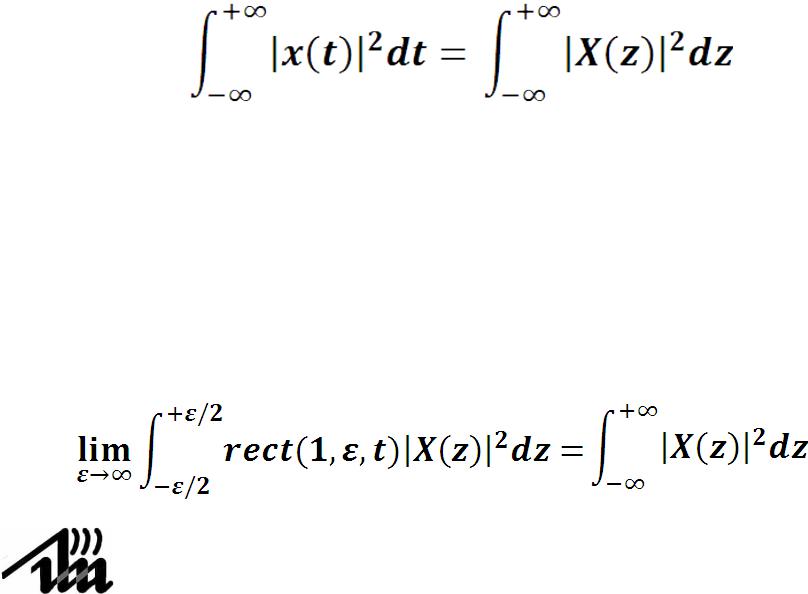
4.12. Равенство Парсеваля
Докажем равенство Парсеваля
Будем предполагать, что x(t) - вещественная функция от вещественной переменной t, а ее Фурье–образ X(z)
– комплексная функция от вещественной переменной z.
При существовании интегралов для правой части верно соотношение
Page 72
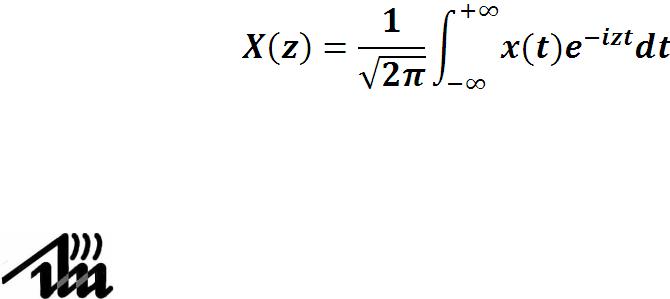
4.12.Равенство Парсеваля
Представим квадрат модуля в удобном виде
/ 2 |
/ 2 |
|
|
|
|||||||
R(1, , z) |
|
X (z) |
|
2 dz |
|
|
|
|
|||
|
|
R(1, , z)X (z)X |
(z)dz |
||||||||
|
|
|
|
|
|||||||
/ 2 |
/ 2 |
|
|
|
|||||||
|
/ 2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
X (z)X |
(z)dz |
|
|
|
|
||||||
/ 2
Запишем Фурье-образы в последнем интеграле
Page 73
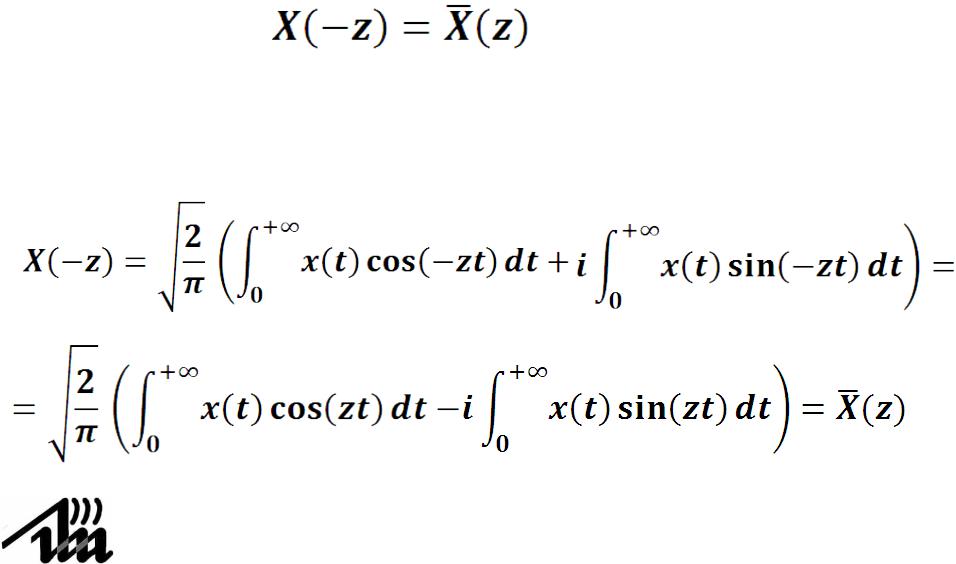
4.12.Равенство Парсеваля
для комплексной функции X(z) от вещественного аргумента z
потому что в выражении через косинус- и синус- преобразования
Page 74
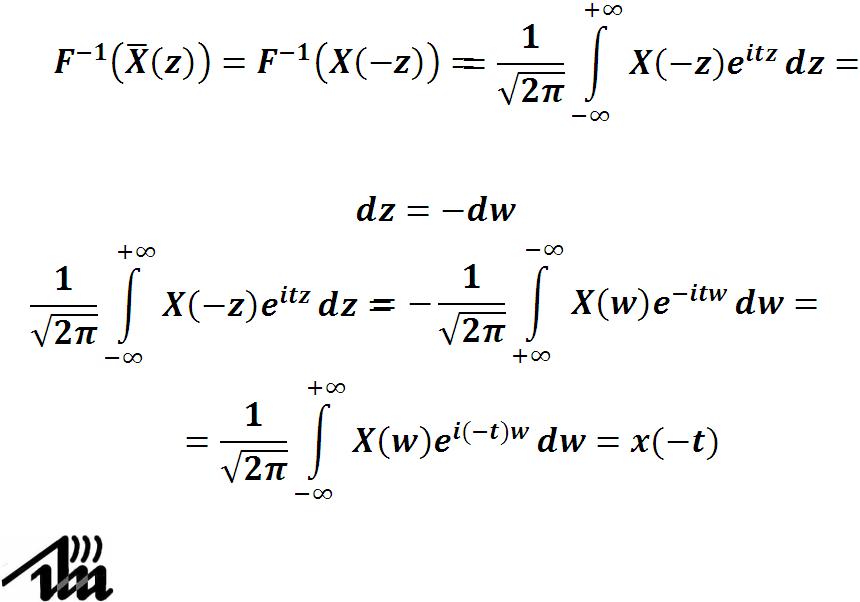
4.12.Равенство Парсеваля
Найдем Фурье-прообраз этой функции
после замены w = -z
Page 75
4.12. Равенство Парсеваля
То есть
Следовательно,
заменим переменную в последнем интеграле
Page 76
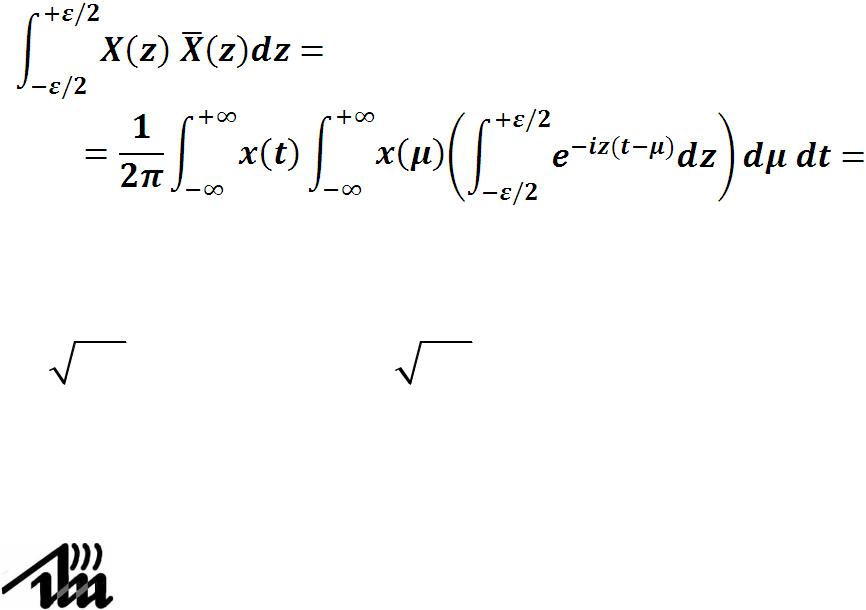
4.12.Равенство Парсеваля
иизменим порядок интегрирования
вернемся к прямоугольному импульсу
|
1 |
|
|
|
1 |
|
|
|
|
|
|
x(t) |
x( ) |
|
|
|
R(1, , z)e iz( t )dz d dt |
2 |
|
2 |
||||||
|
|
|
|
|
|
|||
Выражение в скобках – это преобразование Фурье прямоугольного импульса
Page 77
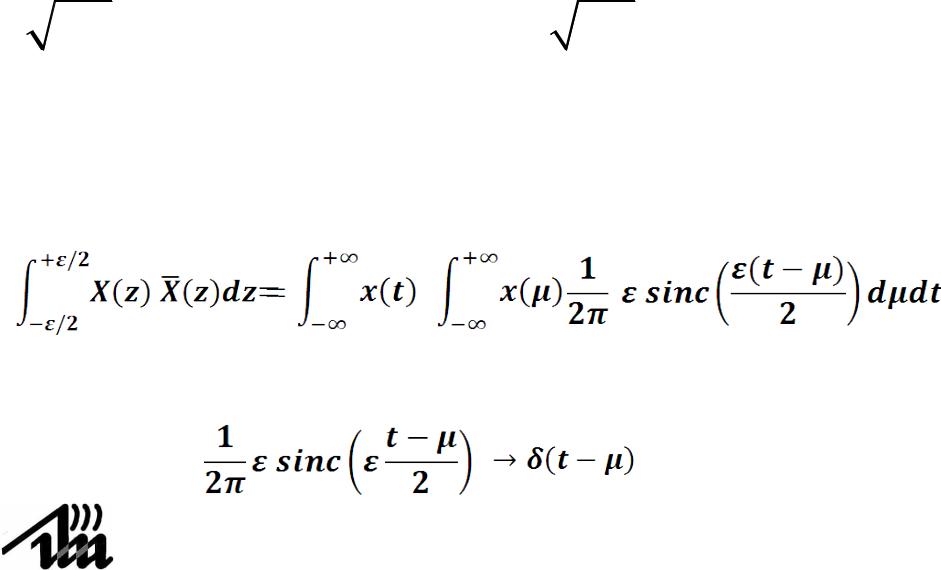
4.12. Равенство Парсеваля
1 |
|
|
|
|
|
|
|
t |
|
|
R(1, |
, z)e |
iz( t ) |
dz |
|||||
|
|
|
|
|
|
||||
2 |
|
|
2 |
sinc |
2 |
||||
|
|
|
|
|
|
||||
Теперь внутренний интеграл (по переменной μ) является сверткой
Перейдем к пределу
Page 78
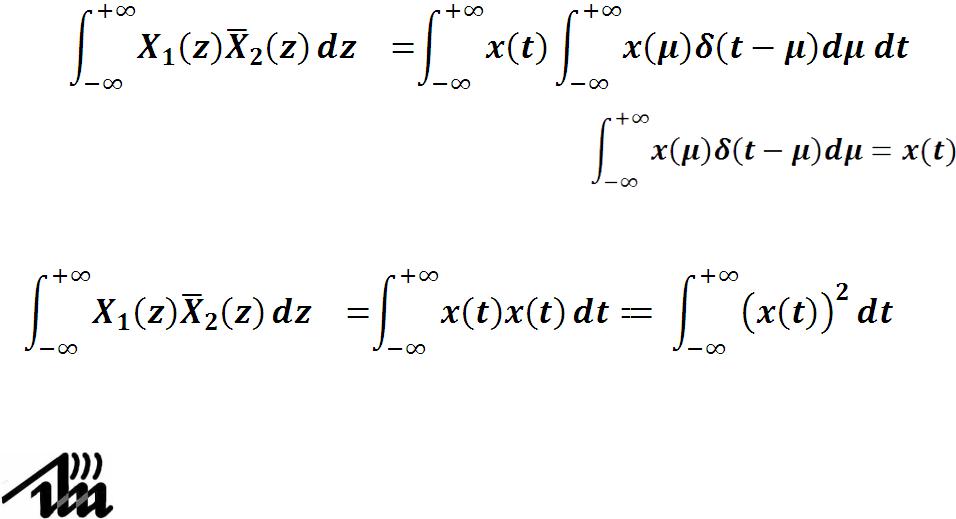
4.12.Равенство Парсеваля
После этого во внутреннем интеграле получаем свертку:
По свойству свертки с импульсом
Окончательно получили:
Page 79
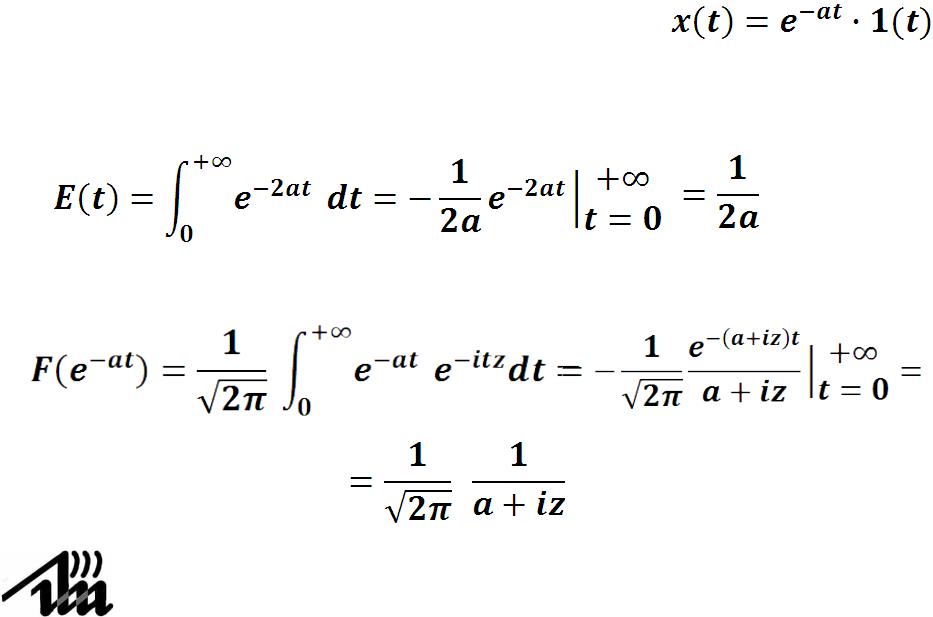
4.13.Применение равенства Парсеваля
Пример. Найти энергию сигнала где параметр a>0.
Энергия, вычисленная во временной области,
в частотной области
Page 80
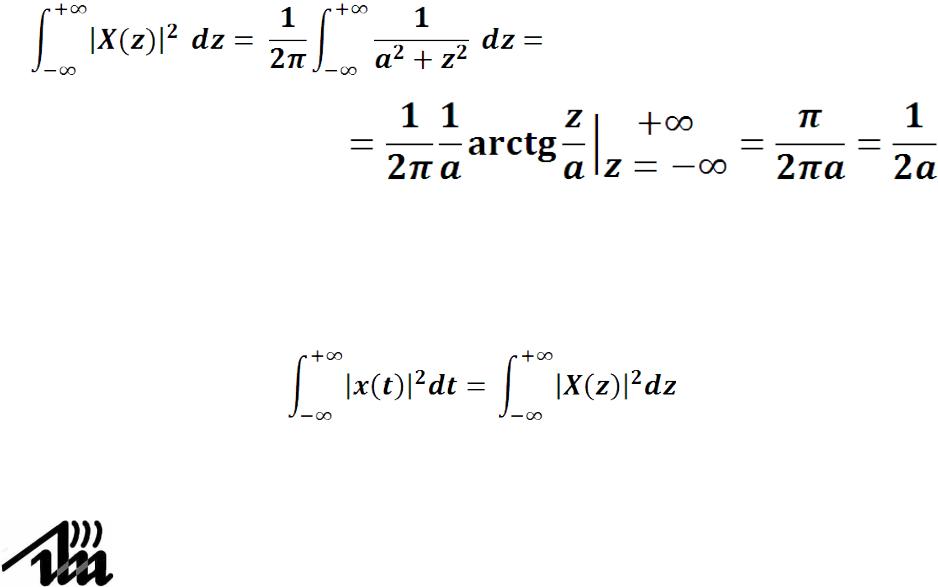
4.13.Применение равенства Парсеваля
Тогда энергия, вычисленная в частотной области
То есть, действительно, энергия, вычисленная в частотной области совпадает с энергией вычисленной во временной области
Page 81